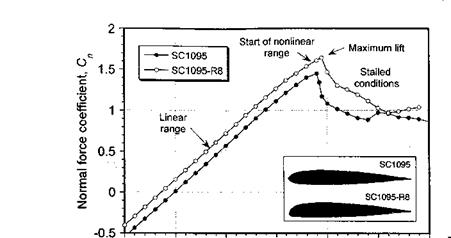
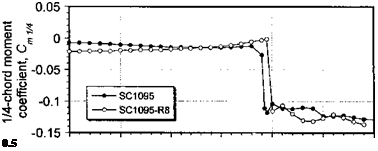
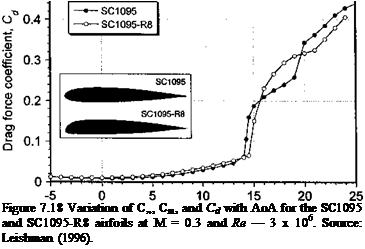
The importance of the airfoil shape on the rotor behavior was well known to Juan de la Cierva – see Cierva & Rose (1931). Cierva originally used a symmetric airfoil section on his Autogiros, but he later changed the airfoil to a highly cambered 17% thick section for better performance. While having a higher stalling AoA, this airfoil also had a higher pitching moment, which resulted in blade twisting and control problems and finally led to a crash of a Cierva Model C-30 Autogiro – see Beavan & Lock (1939). This event, and the generally low torsional stiffness of early wood and fabric helicopter blades, led to the almost universal use of symmetric airfoil sections on helicopters produced prior to 1960. Although symmetric airfoils offered a reasonable overall compromise in terms of maximum lift coefficient, low pitching moments and high drag divergence Mach numbers, they were by no means optimal for attaining maximum performance from the rotor. However, it was not until the early 1960s that a more serious effort came about to improve airfoil sections for use on helicopters.
As early as 1920, a number of different research institutions had begun to examine the characteristics of various airfoils and organize the results into families of airfoils, basically in an effort to determine the profile shapes that were best suited for specific applications. In the United States, NACA conducted a comprehensive and systematic study of the effect of airfoil shape on aerodynamic characteristics. Existing cambered airfoils such as the Clark-Y and Gottingen 398 sections were known from early experiments to have good aerodynamic characteristics. These airfoils were used by NACA as a basis and were found to have geometrically similar shapes when the camber was removed and the airfoils were reduced to the same thickness-tcbchord ratio. NACA then followed a procedure where a
given airfoil could be constructed of a thickness shape that was distributed around a camber line. This allowed the systematic construction of several families of airfoil sections. The use of linearized methods such as thin-airfoil theory also enabled the chordwise aerodynamic loading associated with camber and thickness to be studied, allowing means of designing airfoils to meet specific purposes. The various families of airfoils developed by NACA were then tested in the wind tunnel to document the effects of varying the important geometrical parameters on the airfoil lift, drag, and pitching moment characteristics as a function of AoA, Reynolds number, and Mach number. Variables found to have important effects on the airfoil characteristics included the maximum camber and its distance aft of the leading edge and the leading edge nose curvature (nose radius) of the airfoil. A summary of the results are documented in considerable detail by Abbott et al. (1945) and Abbott & von Doenhoff (1949).
Two of the most popular airfoils used on many early helicopters were the symmetric NACA 0012 and NACA 0015 sections. These airfoils were found to have low pitching moments about the 1 /4-chord and good low-speed as well as high-speed (transonic) performance, giving a relatively high maximum lift and a high drag divergence Mach number. Because these airfoils were also relatively thick, the stiffness of the blade could be maintained while keeping blade weight to a minimum. The upper and lower surfaces of the NACA four-digit symmetrical sections (or thickness envelopes) are described by the polynomial
± — = y, = 5F[0.29690V* – 0.12600* – 0.35160*2 c
+ 0.28430*3 – 0.101503c4], (7.18)
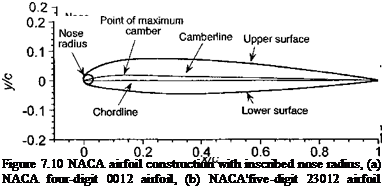
where t/c = t = maximum thickness as a fraction of chord. For example, for the NACA 0012 airfoil t = 0.12. The corresponding leading edge radius of the airfoil is rt = 1.101912. The center for the leading edge radius is found by drawing a straight line through the end of the chord at the origin of the axes and moving a distance along the x axis that is equal to the leading edge radius. The nose radius is then inscribed and faired onto the upper and lower surfaces of the airfoil. The resulting shape is shown in Fig. 7.10(a). The analytic form of the construction lends itself easily to computer generation of the airfoil coordinates – see, for example, Ladson et al. (1995).
A similar approach is used for cambered airfoils, but the mean line (camber line) is used for laying out the airfoil shape. The camberline can be specified as yc — yc(xc). If the slope of the camberline makes an angle в with the chord line, then the airfoil shape is obtained by plotting the thickness distribution at right angles to the slope of the camberline. This will give the upper (jc„, y„) and lower coordinates (xi, yi) of the airfoil:
xu = x — yt sin# and yu = yc + yt cos в, (7.19)
*; = X + у, sin в and у/ = yc — у, cos в, (7.20)
where в = ta. n~l(dyc/dxc). In effect, the shape is being defined as a tangent to a series of circles of radius y, with centers on the camberline. For cambered airfoils, the center for the leading edge radius is found by drawing a straight line through the end of the chord at the origin of the axes but with slope equal to the slope of the camberline at * = 0.005, and then moving along this line a distance that is equal to the leading edge radius. Because of the form of the geometric construction of cambered airfoils, the leading edge part of the nose radius protrudes very slightly forward of the origin at jc =0. As with the symmetric airfoils, the nose radius is then inscribed and faired onto the upper and lower surfaces.
x/c
Various series of mean lines were developed by the NACA, and some of the resulting sections (and derivatives) can be found on modem helicopter blades. Many mean lines, such as the three-digit mean lines, are defined by two equations derived to produce shapes having progressively decreasing camber line slope from the leading edge to the trailing edge. The slope of the camberline is zero at the point of maximum camber (denoted by p) and is constant aft of point m over the trailing edge. The equations for these mean lines are
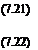
yc = ^k[ [x3 — 3mx2 + m2{3 — m)x from x = 0 to x = m,
_ A <3 _
Ус = ~km (1 — x) from x = m tox = 1. 6
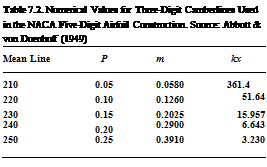
Values of p were selected to give five positions of maximum camber, and values of k were selected to give a design lift coefficient of0.3. The various values of p, m, and&i forthe three – digit camberlines are given in Table 7.2. Figure 7.10(b) shows the graphical construction of the NACA 23012 section, which has been used as a baseline for many modem helicopter airfoil sections. It is derived from the 230 mean line plus the 0012 thickness distribution, and it has a maximum camber at 15% chord and a thickness-to-chord ratio of 12%.
Modifications to the four-digit and five-digit series of NACA airfoil sections include reflex camber to produce zero pitching moment [see Jacobs & Pinkerton (1935)] and changes in the nose radius and position of thickness to improve C/max capability [see Stack
& von Doenhoff (1934)]. The latter sections have seen some use on helicopter rotor and are denoted by a two-digit suffix, such as the NACA 0012-64 and NACA 23012-64. The first integer after the dash indicates the relative magnitude of the nose radius, with a standard nose radius denoted by 6 and a sharp radius by 0. The second digit indicates the position of maximum thickness in tenths of chord.
An early series of special helicopter sections was designed at NACA by Tetervin (1943) and Stivers & Rice (1946). These airfoils, which have NACA 3-H-00 through NACA 10- H-00 series designators, were designed to have lower overall drag over a useful range of lift coefficients but still retain relatively low pitching moments. These airfoils are also discussed by Gessow & Myers (1952).
Another set of NACA airfoils that has seen some use in helicopter applications is the six-digit series. These airfoils were designed to achieve lower drag, higher drag divergence Mach numbers, and higher values of maximum lift. The shapes of these airfoils is such that they are conducive to maintaining an extensive region of laminar flow over the leading edge region and, thereby, lowering skin friction drag, at least over a range of AoA that is limited to low lift coefficients. This is achieved by using camberlines that have a uniform loading from the leading edge to a distance x = a, and thereafter the loading decreases linearly to zero at the trailing edge. The favorable pressure gradients tend to give the airfoils lower drag compared to other airfoils, but these characteristics are easily spoiled by surface contaminants or other transition causing disturbances. There are many designator combinations used in the six-digit number system. For example, consider the NACA 64з – 215 a = 0.5 section. In this case, the number 6 denotes the airfoil series, and the 4 denotes the position of minimum pressure in tenths of chord for the basic symmetric section. The 3 denotes the range of lift coefficient in tenths above and below the design lift coefficient for which low drag may be obtained. The 2 after the dash indicates a design lift coefficient of 0.2, and 15 denotes a 15% thickness-to-chord ratio. These and many other airfoil designators are explained by Abbott & von Doenhoff (1949).
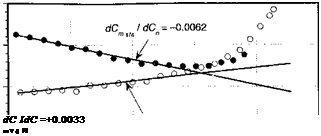
![]() AoA (deg.) -2 0 2 4 6 8
AoA (deg.) -2 0 2 4 6 8![]() m _ _2
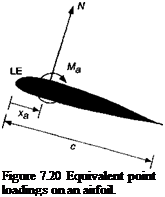
m _ _2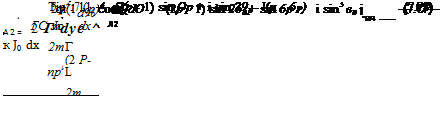


















 -0.05
-0.05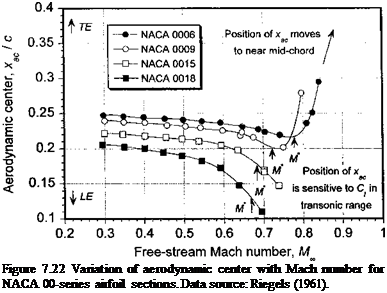

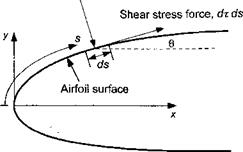
 pi cos в dsi, (7.40)
pi cos в dsi, (7.40)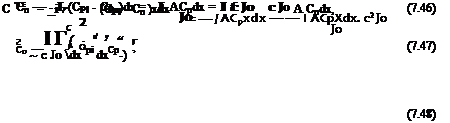
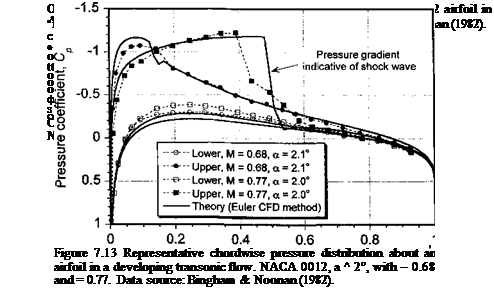
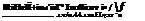
 T c 1 глагііnгт р1пср1; олітаспапЛс tA tbp tV»in_oi Tfnil
T c 1 глагііnгт р1пср1; олітаспапЛс tA tbp tV»in_oi Tfnil