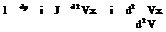Kinematics is the branch of physics that deals with the characteristics of motion without regard for the effects of forces or mass. In other words, kinematics is the branch of mechanics that studies the motion of a body or a system of bodies without consideration given to its mass or the forces acting on it. It describes the spatial position of bodies or systems, their velocities, and their acceleration. If the effects of forces on the motion of bodies are accounted for the subject is termed dynamics. Kinematics differs from dynamics in that the latter takes these forces into account.
To simplify the discussions, let us assume the flow to be incompressible, that is, the density is treated as invariant. The basic governing equations for an incompressible flow are the continuity and momentum equations. The continuity equation is based on the conservation of matter. For steady incompressible flow, the continuity equation in differential form is:
where Vx, Vy and Vz are the velocity components along x-, y – and z-directions, respectively. Equation (2.22) may also be expressed as:
V – V = 0,
V = i — + j— + k —
dx dy dz
and V = iVx + jVy + kVz.
The momentum equation, which is based on Newton’s second law, represents the balance between various forces acting on a fluid element, namely:
1. Force due to rate of change of momentum, generally referred to as inertia force.
2. Body forces such as buoyancy force, magnetic force and electrostatic force.
3. Pressure force.
4. Viscous forces (causing shear stress).
For a fluid element under equilibrium, by Newton’s second law, we have the momentum equation as:
For a gaseous medium, body forces are negligibly small compared to other forces and hence can be neglected. For steady incompressible flows, the momentum equation can be written as:
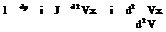
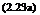 dVx dVx dVx
dVx dVx dVx
Vx —x + Vy —- + Vz —- =
dx y dy dz
Equations (2.23a), (2.23b), (2.23c) are the x, y, z components of momentum equation, respectively. These equations are generally known as Navier-Stokesequations. They are nonlinear partial differential equations and there exists no known analytical method to solve them. This poses a major problem in fluid flow analysis. However, the problem is tackled by making some simplifications to the equation, depending on the type of flow to which it is to be applied. For certain flows, the equation can be reduced to an ordinary differential equation of a simple linear type. For some other type of flows, it can be reduced to a nonlinear ordinary differential equation. For the above types of Navier-Stokes equation governing special category of flows, such as potential flow, fully developed flow in a pipe or channel, and boundary layer over flat plates, it is possible to obtain analytical solutions.
It is essential to understand the physics of the flow process before reducing the Navier-Stokes equations to any useful form, by making appropriate approximations with respect to the flow. For example, let us examine the flow over an aircraft wing, shown in Figure 2.4.
This kind of problem is commonly encountered in fluid mechanics. Air flow over the wing creates higher pressure at the bottom, compared to the top surface. Hence, there is a net resultant force component normal to the freestream flow direction, called lift, L, acting on the wing. The velocity varies along the wing chord as well as in the direction normal to its surface. The former variation is due to the shape of the aerofoil, and the latter is due to the no-slip condition at the wall. In the direction normal to wing surface, the velocity gradients are very large in a thin layer adjacent to the surface and the flow reaches asymptotically to the freestream velocity within a short distance, above the surface. This thin
|
L
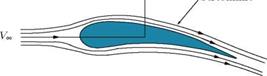
Figure 2.4 Flow past a wing.
|
region adjacent to the wall, where the velocity increases from zero to freestream value, is known as the boundary layer. Inside the boundary layer the viscous forces are predominant. Further, it so happens that the static pressure outside the boundary layer, acting in the direction normal to the surface, is transmitted to the boundary through the boundary layer, without appreciable change. In other words, the pressure gradient across the boundary layer is zero. Neglecting the inter-layer friction between the streamlines, in the region outside the boundary layer, it is possible to treat the flow as inviscid. Inviscid flow is also called potential Bow, and for this case the Navier-Stokes equation can be simplified to become linear. It is possible to obtain the pressures in the field outside the boundary layer and treat this pressure to be invariant across the boundary layer, that is, the pressure in the freestream is impressed through the boundary layer. For low-viscous fluids such as air, we can assume, with a high degree of accuracy, that the flow is frictionless over the entire flow field, except for a thin region near solid surfaces. In the vicinity of solid surface, owing to high velocity gradients, the frictional effects become significant. Such regions near solid boundaries, where the viscous effects are predominant, are termed boundary layers.
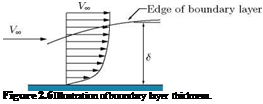
In general, boundary layer over streamlined bodies are extremely thin. There may be laminar and turbulent flow within the boundary layer, and its thickness and profile may change along the direction of the flow. Consider the flow over a flat plate shown in Figure 2.5. Different zones of boundary layer over a flat plate are shown in Figure 2.5. The laminar sublayer is that zone adjacent to the boundary, where the turbulence is suppressed to such a degree that only the laminar effects prevail. The various regions shown in Figure 2.5 are not sharp demarcations of different zones. There is actually a gradual transition from one region, where certain effect predominates, to another region, where some other effect is predominant.
Although the boundary layer is thin, it plays a vital role in fluid dynamics. The drag on ships, aircraft and missiles, the efficiency of compressors and turbines of jet engines, the effectiveness of ramjets and turbojets, and the efficiencies of numerous other engineering devices, are all influenced by the boundary layer to a significant extent. The performance of a device depends on the behavior of boundary layer and its effect on the main flow. The following are some of the important parameters associated with boundary layers.
2.7.1 Boundary Layer Thickness
Boundary layer thickness S may be defined as the distance from the wall in the direction normal to the wall surface, where the fluid velocity is within 1% of the local main stream velocity. It may also be
defined as the distance S, normal to the surface, in which the flow velocity increases from zero to some specified value (for example, 99%) of its local main stream flow velocity. The boundary layer thickness S may be shown schematically as in Figure 2.6.
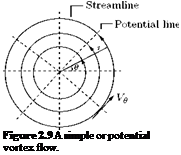











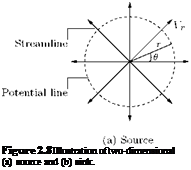
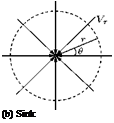
 (2.24)
(2.24) (2.25)
(2.25)