The property which characterizes the resistance that a fluid offers to applied shear force is termed viscosity. This resistance, unlike for solids, does not depend upon the deformation itself but on the rate of deformation. Viscosity is often regarded as the stickiness of a fluid and its tendency is to resist sliding between layers. There is very little resistance to the movement of the knife-blade edge-on through air, but to produce the same motion through a thick oil needs much more effort. This is because the viscosity of the oil is higher compared to that of air.
2.2.3 Absolute Coefficient of Viscosity
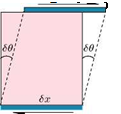
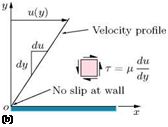
The absolute coefficient of viscosity is a direct measure of the viscosity of a fluid. Consider the two parallel plates placed at a distance h apart, as shown in Figure 2.2(a).
The space between them is filled with a fluid. The bottom plate is fixed and the other is moved in its own plane at a speed u. The fluid in contact with the lower plate will be at rest, while that in contact with the upper plate will be moving with speed u, because of no-slip condition. In the absence of any other influence, the speed of the fluid between the plates will vary linearly, as shown in Figure 2.2(b). As a direct result of viscosity, a force F has to be applied to each plate to maintain the motion, since the fluid will tend to retard the motion of the moving plate and will tend to drag the fixed plate in the direction of the moving plate. If the area of each plate in contact with fluid is A, then the shear stress acting on each plate is F/A. The rate of sliding of the upper plate over the lower is u/h.
These quantities are connected by Maxwell’s equation, which serves to define the absolute coefficient of viscosity p. Maxwell’s definition of viscosity states that:
“the coefficient of viscosity is the tangential force per unit area on either of two parallel plates at unit distance apart, one fixed and the other moving with unit velocity”.
T
(a)
Figure 2.2 Fluid shear between a stationary and a moving parallel plates.
Maxwell’s equation for viscosity is:
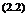
F u
A = gU
Hence,
[ML-1 T-2] = [g] [LT-1L-1] = [g] [T-1]
that is,
[g] = [ML-1T-1] .
Therefore, the unit of g is kg/(m s). At 0 °C the absolute coefficient of viscosity of dry air is 1.716 x 10-5 kg/(ms). The absolute coefficient of viscosity g is also called the dynamic viscosity coefficient.
The Equation (2.2), with g as constant, does not apply to all fluids. For a class of fluids, which includes blood, some oils, some paints and so called “thixotropic fluids,” g is not constant but is a function of du/dh. The derivative du/dh is a measure of the rate at which the fluid is shearing. Usually g is expressed as (N. s)/m2 or gm/(cm s). One gm/(cm s) is known as a poise.
Newton’s law of viscosity states that “ the stresses which oppose the shearing of a fluid are proportional to the rate of shear strain,” that is, the shear stress т is given by:
where g is the absolute coefficient of viscosity and du/dy is the velocity gradient. The viscosity g is a property of the fluid. Fluids which obey the above law of viscosity are termed Newtonian fluids. Some fluids such as silicone oil, viscoelastic fluids, sugar syrup, tar, etc. do not obey the viscosity law given by Equation (2.3) and they are called non-Newtonian fluids.
We know that, for incompressible flows, it is possible to separate the calculation of velocity boundary layer from that of thermal boundary layer. But for compressible flows it is not possible, since the velocity and thermal boundary layers interact intimately and hence, they must be considered simultaneously. This is because, for high-speed flows (compressible flows) heating due to friction as well as temperature changes due to compressibility must be taken into account. Further, it is essential to include the effects of viscosity variation with temperature. Usually large variations of temperature are encountered in high-speed flows.
The relation m(T) must be found by experiment. The voluminous data available in literature leads to the conclusion that the fundamental relationship is a complex one, and that no single correlation function can be found to apply to all gases. Alternatively, the dependence of viscosity on temperature can be calculated with the aid of the method of statistical mechanics, but as of yet no completely satisfactory theory has been evolved. Also, these calculations lead to complex expressions for the function /г(Т). Therefore, only semi-empirical relations appear to be the means to calculate the viscosity associated with compressible boundary layers. It is important to realize that, even though semi-empirical relations are not extremely precise, they are reasonably simple relations giving results of acceptable accuracy. For air, it is possible to use an interpolation formula based on D. M. Sutherland’s theory of viscosity and express the viscosity coefficient, at temperature T, as:
M = ( T_3/2 To + S Mo To) T + S
where mo denotes the viscosity at the reference temperature T0, and S is a constant, which assumes the value 110 K for air.
For air the Sutherland’s relation can also be expressed [1] as:
where T is in kelvin. This equation is valid for the static pressure range of 0.01 to 100 atm, which is commonly encountered in atmospheric flight. The temperature range in which this equation is valid is from 0 to 3000 K. The absolute viscosity is a function of temperature only because, in the above pressure and temperature ranges, the air behaves as a perfect gas, in the sense that intermolecular forces are negligible, and that viscosity itself is a momentum transport phenomenon caused by the random molecular motion associated with thermal energy or temperature.











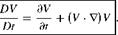 (2.21)
(2.21)