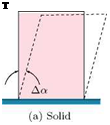
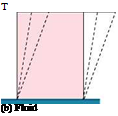
Boundary layer is a thin layer, adjacent to a solid surface, in which the flow velocity increases from zero to about 99% of the freestream velocity, as shown in Figure 1.14.
The boundary layer may also be defined as a thin layer adjacent to a solid surface where the viscous effects are predominant. Thus, inside the boundary layer the effect of viscosity is predominant. Outside the boundary layer the effect of viscosity is negligible. Also, greater the Reynolds number the thinner will be the boundary layer, and we have practically the case of an inviscid flow past an object. But, however small the viscosity may be, the plate is subjected to a tangential traction or drag force acting in the direction of flow velocity. This force is known as the skin friction or the frictional drag, and this force can never be completely eliminated. On the other hand, the flow outside the boundary layer behaves like an inviscid flow.
|
Ко
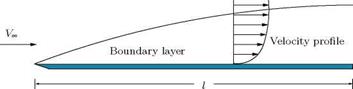
Figure 1.14 Boundary layer on a flat plate.
|
|

Figure 1.15 An aerofoil in an uniform flow.
|
For flow past a bluff body, such as a circular cylinder, an eddying wake forms behind the cylinder, greatly increasing the drag. The problem of flow separation or break away of the boundary layer from a bluff body can be minimized by streamlining the body. For properly streamlined bodies the boundary layer will not break away and the wake will remain almost insignificant. This has been achieved in the profiles like that shown in Figure 1.15 which are generally referred to as aerofoils.
For aerofoils there is a narrow wake but, to a first approximation, the problem of the flow past such a streamlined shape can be assumed as an inviscid flow past the body. In other words, the flow past an aerofoil can be regarded as flow without wake. The above considerations give rise to the following general observations:
1. It is found that to delay the breaking away of the boundary layer from the region where the fluid is moving against increasing pressure (that is, adverse pressure gradient, as in the case of the rear of a circular cylinder) the flow should turn as gradually as possible. To enable this gradual turning of flow, the body should have a large radius of curvature.
2. It is essential to keep the surface of the object smooth, because even small projections above the surface (in general) may disturb the boundary layer considerably, causing a breaking away of the flow. Furthermore, a projection such as a rivet, whose head projects above the boundary layer, may entirely alter the character of the flow. An exaggerated flow over an aerofoil with such a rivet head is schematically shown in Figure 1.16.
3. Good streamlined shapes will have the breaking away of the flow just close to the trailing edge.
|

Figure 1.16 Flow separation caused by a rivet head projection.
|
1.10 Summary
Aerodynamics is the science concerned with the motion of air and bodies moving through air. In other words, aerodynamics is a branch of dynamics concerned with the steady motion of air, particularly when it interacts with a moving object. The forces acting on the bodies moving through the air are termed aerodynamic forces.
The aerodynamic force Fad can be resolved into two component forces, one at right angles to V and the other opposite to V. The force component normal to V is called lift L and the component opposite to V is called drag D.
A streamlined body is that for which the skin friction drag accounts for the major portion of the total drag, and the wake drag is very small.
A bluff body is that for which the wake drag accounts for the major portion of the total drag, and the skin friction drag is insignificant.
The main lifting system of an aircraft consists of two wings which together constitute the aerofoil. The tail plane also exerts lift. The ailerons on the right and left wings, the elevators on the horizontal tail, and the rudder on the vertical tail are control surfaces.
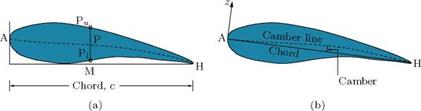
The distance between the wing tips is called the span. The section of a wing by a plane parallel to the plane of symmetry is called a profile.
Chord of any profile is generally defined as an arbitrarily fixed line drawn in the plane of the profile. The chord has direction, position, and length.
For a cylindrical aerofoil (that is, a wing for which the profiles are the same at every location along the span), the chord of the aerofoil is taken to be the chord of the profile in which the plane of symmetry cuts the aerofoil. In all other cases, the chord of the aerofoil is defined as the mean or average chord located in the plane of symmetry.
The aspect ratio of a wing is the ratio of its span 2b to chord c.
• Camberline of an aerofoil is essentially the bisector of its thickness.
• Camber is the deviation of the camberline from the chord, namely the shortest line joining the leading and trailing edges of the aerofoil profile.
• The local camber can vary continuously from the leading edge to the trailing edge. Therefore, the maximum camber is taken as the representative camber. That is, the maximum ordinate of the camberline from the chord is taken as the camber of an aerofoil.
When an aircraft travels in the plane of symmetry (that is, the direction of flight is parallel to the plane of symmetry), the angle between the direction of motion and the direction of the chord of a profile, is called the geometrical incidence of the profile, denoted by the Greek letter a. The angle a is also called angle of attack.
Aerodynamic force on an aircraft is the force due to the pressure distribution around it, caused by the motion of the aircraft. Thus, the gravity does not enter into the specification of aerodynamic force.
Mach number is the ratio of local flow speed to the local speed of sound or the ratio of inertial force to elastic force. It is a measure of compressibility. For an incompressible fluid the M = 0.
The dimensionless group (Vl/v) is called the Reynolds number Re. Reynolds number is the ratio of inertial force to viscous force. For an inviscid fluid Re = to. For air, v is small and Re is large unless Vl is small.
The dimensionless number:
is called the (dimensionless) coefficient of the aerodynamic force Fad.
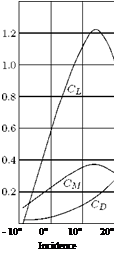
The important aerodynamic forces and moment associated with a flying machine, such as an aircraft, are the lift L, the drag D, and the pitching moment M. The lift and drag forces can be expressed as dimensionless numbers, popularly known as lift coefficient CL and drag coefficient CD, by dividing L and D with 1 pV2S. Thus:
 L
L
2 pV 2S
D
2 pV 2S
The pitching moment, which is the moment of the aerodynamic force about an axis perpendicular to the plane of symmetry (about y-axis in Figure 1.3), will depend on the particular axis chosen. Denoting the pitching moment about the chosen axis by M (note that M is also used for denoting Mach number, which is the ratio of local flow speed and local speed of sound), we define the pitching moment coefficient as:
Boundary layer is a thin layer, adjacent to a solid surface, in which the flow velocity increases from zero to about 99% of the freestream velocity. The boundary layer may also be defined as a thin layer adjacent to a solid surface where the viscous effects are predominant. Thus, inside the boundary layer the effect of viscosity is predominant. Outside the boundary layer the effect of viscosity is negligible.
For flow past a bluff body, such as a circular cylinder, an eddying wake forms behind the cylinder, greatly increasing the drag. The problem of flow separation or break away of the boundary layer from a bluff body can be minimized by streamlining the body. For properly streamlined bodies the boundary layer will not break away and the wake will remain almost insignificant.
Exercise Problems
1. An aircraft of total mass 10000 kg cruises steadily at an altitude. If the aerodynamic efficiency is 4, find the thrust required to propel the aircraft.
[Answer: 24.525 kN]
2. An aircraft of mass 3000 kg in a steady level flight is at an angle of incidence of 5° to the freestream. Determine the thrust generated by the engine.
[Answer: 2574.8 N]
3. An aircraft weighing 200 kN is in level flight at sea level with a speed of 600 km/h. The wing span and chord are 8 m and 1.8 m, respectively. Determine the lift coefficient of the wing.
[Answer: 0.816]
4. Determine the speed of sound in air at sea level conditions.
[Answer: 340.3 m/s]
5.
If the aerodynamic efficiency of an aircraft in a steady flight is 10, determine the incidence of the wing to the freestream direction.
6. A sail plane of mass 270 kg flies straight and level with an incidence of 4°. Determine the aerodynamic force acting on the wings and the aerodynamic efficiency.
[Answer: 2655.17 N, 14.30]
7. A wing of rectangular planform has 10 m span and 1.2 m chord. In straight and level flight at 240 km/h the total aerodynamic force acting on the wing is 20 kN. If the aerodynamic efficiency of the wing is 10, calculate the lift coefficient. Assume air density to be 1.2 kg/m3.
[Answer: CL = 0.622]
Reference
1. Rathakrishnan, E., Applied Gas Dynamics, John Wiley & Sons Inc., New Jersey, 2010.

![]()















 Ch°irl &
Ch°irl &