Rapid Prototyping
Rapid prototyping is a process by which the airplane main lifting component, the wing, can be sized and its weight estimated. For a composite wing, given the span and the chord, the weight depends on its volume, and the density of the foam used to build the wing core, and its surface area, and the density of the carbon fiber/glass fiber materials to make the wing skin. The weight of the other components, fuselage, tail and landing gear are also estimated, and by subtraction from the gross weight at take-off, the payload prediction is obtained and a flight raw score calculated. This code is a “cookie-cutter” for the wing as it estimates the best chord size for a given span and wing profile lift characteristics. The following assumptions are made to simplify as much as possible the analysis:
(i) rectangular wing with span b and chord c
(ii) elliptic circulation (the lower the aspect ratio AR, the more appropriate it is)
(iii) drag coefficient defined by
CL
Cd — Coo + ^ (11.24)
n eAR
(iv) engine thrust T(V) — T0 – KV
(v) rolling friction is neglected (although it had been implemented when taking-off from grass field)
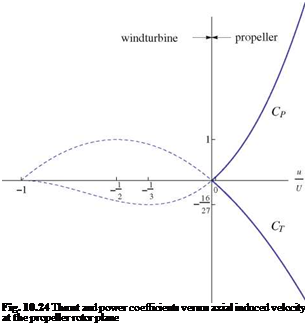
The aspect ratio is defined as AR = b2/S where S is the wing area and reduces to AR = b/c for a rectangular wing. The zero-lift drag coefficient CD0 is estimated from the airplane wetted area and parasitic drags (landing gear primarily). The efficiency factor, e, is close to unity (e = 0.9) for a wing of medium aspect ratio, AR = 10 or so, but could be closer or even larger than one with winglets. The lift coefficient CL depends on the setting angle of the wing on the fuselage which determines the wing incidence during the rolling phase. The propeller is selected to match the engine and to produce a high static thrust T0 in (N) at high nominal rpm, measured with a fish scale. As the airplane accelerates, the thrust decreases. For simplicity, we use the actuator disk theory to estimate T(V) at low speeds. A more accurate approach would be to measure the thrust of the propeller placed in a wind tunnel or to use a propeller code (if the engine power were known as a function of rpm). Let Ub be the average axial induced velocity at the rotor, then power and thrust are given by
P = 2np R2(V + Ub)2Ub (11.25)
T = 2npR2(V + Ub)Ub, ^ T0 = 2npR2Ub2 (11.26)
Assuming that the power remains constant at low speeds, the condition dP = 0 reduces to
![]()
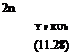 dUb 2Ub
dUb 2Ub
~dV = – V + 3Ub
On the other hand, the change in thrust at low speeds reads
dT 2 ( dUb 2 V + Ub
= 2np R2 Ub + (V + 2Ub) b =-2np R2 b-Ub
dV dV V + 3Ub
Upon elimination of Ub one finds
|
|
|
|
|
|
|
|
![]()
with T0 and K, the model can be further developed. Newton’ second law reads
d2x dV dV dx dV 1 2
M 2 = M = M = MV = T0 – KV –pV2ArefCo (11.30)
dt2 dt dx dt dx 2
The last term corresponds to the total aerodynamic drag, i. e. viscous drag and induced drag, D = 1 p V2 ArefCD. One can separate the variables and write
MVdV
T0 – KV – 1 pArefCDV2
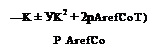 |
||
Let У1 and V2 be the roots of the quadratic equation for V
The positive root, V2, corresponds to the maximum velocity obtained as asymptotic limit over an infinite rolling distance (V1 has no physical significance). The equation can now be written as
VdV 1 V1 V2 1 dx
(V — V1)(V — V2) V1 — V2 V — V1 V — V2 2PAref D M
(11.33)
Upon integration from V = 0 for a finite rolling distance (say, L = 55 m = 180 ft to allow for rotation before take-off) one finds
VT—Vi (V2‘n(— V‘ln(^)) = 1PV2ArefCoM (1134)
This is an implicit equation for the take-off velocity V. It can be solved iteratively as
(11.35)
where n = 0, 1,… is the iteration index. An initial guess is V(0) = V2.
Given a maximum lift coefficient CLmax for the wing at take-off, the drag D at take-off is known and the climb angle в can be calculated as
The wing span being given (and changed if the rules allow), the code performs a loop on the wing chord by steps of 1 cm. For each chord size, the wing weight is calculated and the gross weight of the airplane estimated. The take-off velocity is then calculated, using the above iterative formula. Finally the climb angle is obtained and the loop on the chord is terminated when the climb angle is в > 3°. This value is chosen to allow the airplane to clear the runway, but also to account for uncertainties. The flight score is predicted from the payload.
Fine tuning of the configuration is carried out with the next level of modelisation.













 em is the wing efficiency or efficiency factor. For a medium aspect ratio wing (AR ~ 10) a value em = 0.9 is acceptable, but values that are higher or even larger than one are possible if winglets are added. The total drag of the main wing is thus
em is the wing efficiency or efficiency factor. For a medium aspect ratio wing (AR ~ 10) a value em = 0.9 is acceptable, but values that are higher or even larger than one are possible if winglets are added. The total drag of the main wing is thus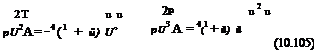
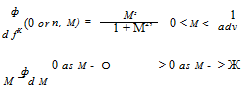 (10.108)
(10.108)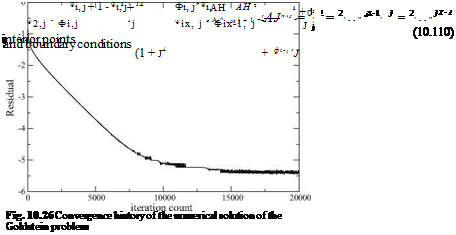

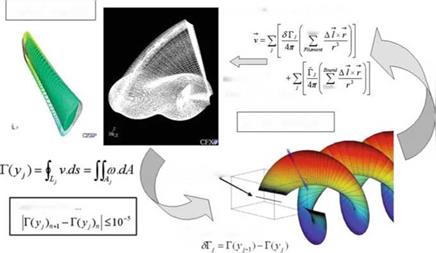 Biot-Savart Law (discrete)
Biot-Savart Law (discrete)