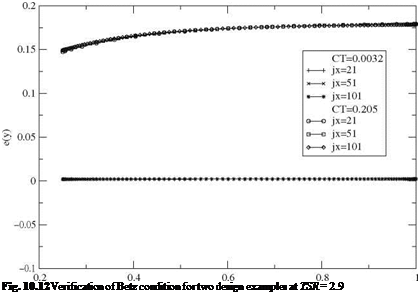
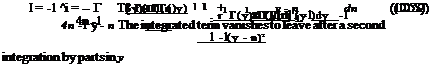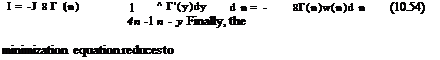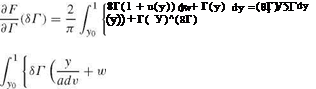Tower Interference Model
Two configurations are considered in this section, one in which the rotor is upstream of the tower and the other in which it is downwind of the tower. These situations are quite different from a physical point of view. In the former, the inviscid model is appropriate and the tower interference consists in a blockage effect due to the flow slowing down and stagnating along the tower. In the latter, the blade crosses the viscous wake of the tower, a region of rotational flow with low stagnation pressure, the extent of which as well as steadiness characteristics depend on the Reynolds number.
In the upwind configuration, the tower interference is modeled as a semi-infinite line of doublets aligned with the incoming flow. One can show that the velocity potential for such a flow is given by
where r = r/R is the dimensionless tower radius. The coordinate system is aligned with the wind, the X-axis being aligned and in the direction of the incoming flow, the Z-axis being vertical oriented upward and the Y-axis completing the direct orthonormal reference system. See Fig. 10.18.
In the downwind configuration, an empirical model due to Coton et al. [15] is used. The above potential model of the tower is applied almost everywhere, but when a blade enters the narrow region |Y | < 2.5 r corresponding to the tower shadow, the tower induced axial velocity is set to ФX = -0.3F and the other two components are set to zero.
The velocity field induced by the tower is given by VФ = (Фх, Фу, Фу). In the
rotating frame, a point on blade 1 has coordinates (0, yj, 0). Let d = d/R be the
dimensionless distance of the rotor from the tower axis. A negative value indicates upwind configuration, while a positive value indicates downwind case. In the fixed frame of reference, such a point has coordinates given by
/ X / cos в – sin в 0 / d
Y = sin в cos в 0 yj sin ф (10.101)
Z 0 0 1 yj cos ф
Using the same transformation, the tower-induced velocities at the blade can be calculated with the help of the components of the unit vectors in the rotating frame:
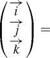 / cos в sin в 0 I
/ cos в sin в 0 I
– sin в sin ф cos в sin ф cos ф I J I (10.102)
sin в cos ф – cos в cos ф sin ф J
where ( i, j, k ) and (J, ~J, ~K) are the unit vectors in the rotating frame and the
wind frame respectively. For blade 1 the induced velocities are Uj, i = (V Ф. i ) and
wj, i = (VФ. k ). Application of this formula to the incoming flow V = (1, 0, 0) provides the axial and azimuthal components of the unperturbed flow in the rotating frame, again for blade 1
u = (V. J) = cos в (10.103)
w = (V Л ) = sin в cos ф (10.104)













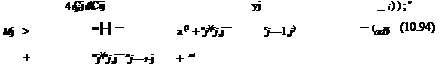
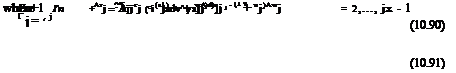
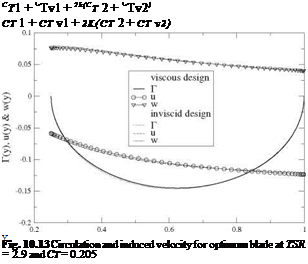
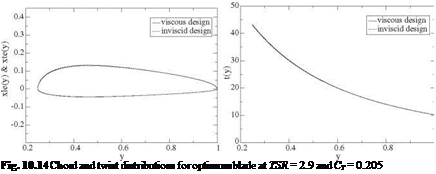
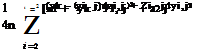
 Ct = Гк (1 + Uk) yk (Пк – Пк-1)
Ct = Гк (1 + Uk) yk (Пк – Пк-1) —————- (о* + “’j)(пj- пj-1)
—————- (о* + “’j)(пj- пj-1)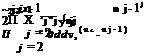
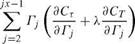 Ct 1 + 2Cr2 + X (Ct 1 + 2Ct2)
Ct 1 + 2Cr2 + X (Ct 1 + 2Ct2)