Supersonic Linearized Theory (Mo > 1)
The wave drag coefficient (Cd)a=0 is given by
|
dx 16 ґв[8] c 3в Vc/ |
(Cd )a=0 = (f’+(X )f + (f ‘-(X ))"
as seen in class.
Hence the lift and wave drag coefficients are:
4a
Cl (a) = — = 0.0403
P
|
16 /e2 4a2 Cd(a) = 3в U + IT = a0315 |
3в c) в
The lift and wave drag upper bounds for the fin are
12
L = 2 pV[9] 2bc Cl = 106 N
D = 2pV2bc Cd = 82.9 N
15.3.1 Lifting Line Theory (3-D Inviscid Flow)
15.3.2.1 Induced Drag in Cruise The induced drag Di in (N) is given by
1 2 c2l
Di = – pV 2 5—– —
i Г neAR
|
1 1 pV2neb2 |
The equilibrium equation along the vertical axis during horizontal cruise in dimensional form (neglecting the lift of the tail) reads:
 |
The drag penalty is = 0.21, i. e. a 21 % increase in induced drag.











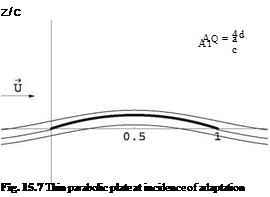
 Improved Lift of a Rectangular Wing
Improved Lift of a Rectangular Wing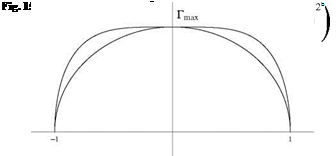
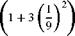
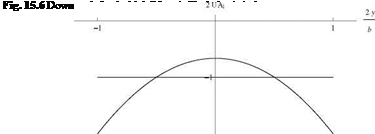
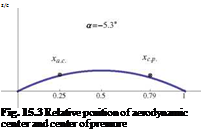

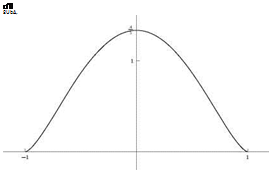 Fig. 15.2 Distribution of circulation
Fig. 15.2 Distribution of circulation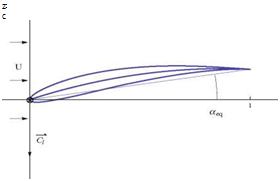 aeq is found to be
aeq is found to be