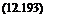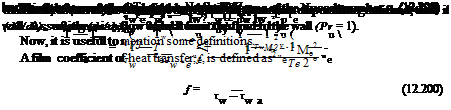Hydraulic Analogy
The equations of unsteady two dimensional compressible inviscid flows are analogous to the shallow water equations where the height of the water corresponds to the density of the compressible fluid. To show such analogy, we will start with the isentropic Euler equations in conservative form
![]()
![]()

+ dU + d-f. = о
dx dy
dpu dpu2 dpuv dp
dt + dx + dy dx
dpv dpuv dpv2 d p
dt + dx + dy dy
|
|
|
P_ P0 |
The above equations imply conservation of mass, momentum and entropy. Energy is not conserved in general. Only for smooth flow, energy will be conserved.
Next, consider a thin layer of water over a flat smooth plate, where the height of the water is given by h (x, y, t).
The conservation of mass requires
Since pw = const, it cancels out and the equation becomes similar to the compressible flow continuity equation, where p is replaced by h.
The momentum equations for the column of water with height h is given, ignoring the viscous effects, by
![]() dpwhuv dpwhuv dpwhv2 dh 1 dh2
dpwhuv dpwhuv dpwhv2 dh 1 dh2
+ + = —pwgh = — pw9
dt dx dy dy 2 dy
Once again, pw cancels out.
Assuming small variations of the water surface and ignoring the vertical acceleration, the pressure is governed by the hydrostatic equation
p = Patm + pw9(h — z), 0 < z < h (13.26)
where z is the elevation of a point above the flat plate.
Hence
On the other hand, from isentropic relation of compressible flows,
dp = dp d£ = 2 df_ dp = dp dp _ 2dL (13 28)
dx dp dx a dx ’ d y dp d y a d y ‘
where a2 = yRT. Hence the analogy holds if a2 corresponds to gh. In this case, the Mach number M = V/a corresponds to the Froude number F = V/л/gh of the shallow water waves where л/gh is the speed of surface waves due to small disturbances.
Notice the pressure of compressible flow corresponds to h2, hence the analogy holds only for y = 2. In this case the temperature of the compressible flow corresponds to h.
To summarize these relations, the different non dimensional quantities for compressible and shallow water flows are given in Table 13.1, where subscript r stands for reference quantities
 |
 |
There are several special cases of interest including
(i) Quasi-one dimensional unsteady flows in nozzles,
(ii) Two dimensional steady external and internal flows,
(iii) irrotational flows.
The above derivation shows that the analogy is valid for rotational flows where vorticity may be generated due to the variation of the total enthalpy according to Crocco’s relation. One can consider the special case where vorticity vanishes and a potential flow exists for both steady as well as unsteady phenomena. In all cases, the flow is assumed isentropic. In the following, hydraulic jumps (corresponding to shock relations of compressible flows) will be studied.
The propagation of sound corresponds to the propagation of an infinitesimal gravity wave, since
![]() (13.29)
(13.29)
corresponds to
with a2 = gh.
Also, the linearization of the shallow water equation yields the classical wave equation
where a0 = gh0.
Real time observation is possible since g = 9.81 m/s2 and for h = 0.01 m, a = 0.3 m/s. In fact, shallow water experiment can be performed at the kitchen sink!
For smooth steady flows, one can obtain the isentropic relation and corresponding shallow water equations. For example
Supersonic (M > 1) and subsonic (M < 1) flows correspond to supercritical (F > 1) and subcritical (F < 1) flows.
The analogs of shock waves are called hydraulic jumps. Moving with the discontinuity and considering the relative normal velocity, one can derive the following steady relations
u 1 h 1 = u2h2 = m (13.33)
To evaluate the momentum balance, a control volume is used as shown in Fig. 13.3. Friction on the bottom surface is neglected.
The net acting force per unit span in the x-direction due to pressure is
J Pwg(h1 – z) dz – J Pwg(h2 – z) dz = 1 pwg (h2 – h^ (13.34)
Hence, the rate of change of x-momentum reads
Pwu2h2 – Pwu2h1 = 2Pwg ^2 – h^ (13.35)
or
u2hi + – ghf = uh2 + – gh2 = n (13.36)
The above equations can be solved for (u, h) = (u2, h2) given (u1, h 1) as follows uh = m, and u2h + 1 gh2 = n (13.37)
|
Fig. 13.3 Hele-Shaw flow past a rectangular block (from en. wikipedia. org) |
![]()
![]() (13.44)
(13.44)
The solution with F1 < 1 and h/ h 1 < 1 is excluded. It corresponds to an expansion shock. To see that analogy, consider the specific energy (see White [7])
![]()
![]()
![]()
 |
|
1 2 1 m2
E = gh + 2 U = gh + 2 H2
For a given m (discharge), there are two possible states for the same E, see the sketch in Fig. 13.4 and their relation is plotted in Fig. 13.5.
There is a minimum value of E at a certain value of h called the critical value. Setting dE/dh = 0, Emin occurs at g – m2/h3 = 0, or hc = [m2/g)1/3 and Emin = ghc + m2/(2hC).
 |
At the critical depth, m2 = ghl = c2h2, where c0 = Vghc and F = 1.
For E < Emi„, no solution exists and for E > Emin two solutions are possible with h > hc and u < co as well as h < hc and u > c0. The analogy with Mach waves is clear with the angle of the wave given by
sin g = — (13.46)
u
Now, across the jump
This equation shows that dissipation loss is positive only if h2 > h 1, a requirement implied by the second law of thermodynamics.
A more consistent analysis would be based on the total enthalpy (and not just potential and kinetic energy)
h _ p/pr 1 1 u 2
![]()
![]() u2 ~ (Y – 1)p/Pr M2 + 2 Mr
u2 ~ (Y – 1)p/Pr M2 + 2 Mr
The corresponding quantity for shallow water is
H _ h 1 1 / u 2
m2 hr F2 + 2 ur
The total enthalpy should decrease for steady isentropic Euler shocks (see [8]) and hence expansion shocks are excluded and the same is true for hydraulic jumps. Again, from the conservation of mass across the hydraulic jump
u і h і = u2h2 = m (13.50)
and from the momentum balance
2 19 9 19
u2h1 + gh2 = u2h2 + gh2 = n (13.51)
one can show, upon elimination of h that
1 ![]()
![]()
![]() m2 1 m2
m2 1 m2
mu1 + g 2 = mu2 + g 2
2 u 21 2 u 22
Introducing the jump notation [a] = a2 – a1, one can write
< u > + gm = 0 (13.53)
2 u2
Hence
![]()
 <u>
<u>
T
M
The latter is analogous to the Prandtl relation for normal shock of compressible fluid flow.
Hydraulic analogy can provide experimental demonstration of compressible flow phenomena using a device called water table, which consists of an inexpensive sheet of glass with suitable sides. Either a model is moved in a thin layer of water or the
model is fixed and the water flows around it. The analogy is particularly useful for transonic flows including shocks. Examples are:
(i) Transonic flows in convergent/divergent nozzle at design and off-design conditions,
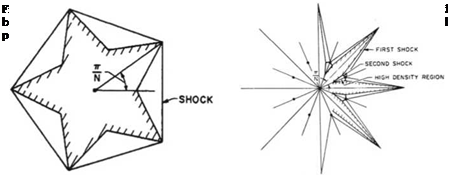
(ii) Steady two dimensional supersonic flows over airfoils (flat plate, parabolic or diamond airfoils). Compression shocks and expansion fans are easily identified. Attached and detached shocks as well as fish tail shocks can be observed, including wave reflected from the walls,
(iii) Unsteady flows, including accelerated and decelerated as well as oscillating airfoils.
There are limitations, of course. Strong shocks are not well represented. The assumptions that vertical accelerations are small, the viscous force exerted by the horizontal bottom is negligible and the vertical variation of the velocity can be neglected in the continuity equation are questionable if quantitative results are required. In general, separated flows are not representative since the Reynolds numbers are very different in water and compressible flows. For more details, the reader is referred to Oswatitsch [9],Loh [10], Thompson [11] and White [7].
















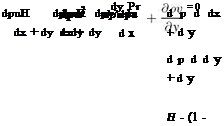
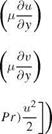
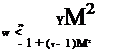 (12.223)
(12.223)