In general, the study of lifting surface problems can be performed with the help of electric tanks.
The low and high aspect ratio (AR) wings are of special interest since the formulation will reduce to two-dimensional problems.
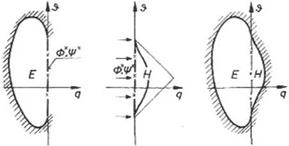
In the case of slender wings and slender bodies at angle of attack, the flow can be decomposed into axial and normal components. The cross flow at the end section can be easily studied by electric analogy (as a special case of two-dimensional flows with a = 90°) using polar coordinates.
On the other hand, the lifting line theory for high AR wings can be studied using the Trefftz plane. The Prandtl integro-differential equation is given by
where the downwash at the lifting line is given by
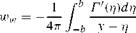 (13.75)
(13.75)
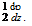 Notice that Г(-Ь) = Г(Ь) = 0 and 7b dГ(п) = 0. A potential function can be
Notice that Г(-Ь) = Г(Ь) = 0 and 7b dГ(п) = 0. A potential function can be
introduced in the Trefftz plane such that Г(у) = 2^> and w Now, p is zero outside the span (-b, b), and in between
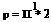
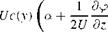 (13.76)
(13.76)
Also, p need only to be considered in a half-plane since p(y, -z) = – p(y, z).
The boundary conditions along the axis can be simulated using a distribution of electrodes to impose the above mixed boundary condition as well as the Dirichlet condition, in a plane tank of large dimensions.
Nonlinear local lift coefficient in the neighborhood of maximum lift can also be considered using successive approximations.
Moreover, wind tunnel wall effects can be readily shown using dp/dn = 0 on solid walls and p = const. in open section, where the pressure is constant across the wall boundaries.
Analog study of propeller’s performance following Goldstein’s analysis [16] is also possible. The potential of the velocity induced by the trailing vortex sheets satisfies the equation
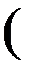 1 д дф 1 д2ф д2ф
1 д дф 1 д2ф д2ф
r dr dr + r2 дв2 + дz2
where the z-axis coincide with the propeller axis. If the propeller has p blades, the trailing vortex system is composed of p helicoids of geometric pitch h = 2nw/w, where w is the translation velocity along the z-axis and w is the angular speed of rotation.
The equation of these helicoidal surfaces is defined by z k
в – = 2п, k = 0, 1,…p – 1, 0 < r < R (13.78)
A P
where A = w/(wR), R is the radius of the propeller. The potential equation can be written in terms of £ = r/R and Z = в – z/x as follows
Moreover, the periodicity of the field with respect to £ (period 2п/p) and the antisymmetry of ф with respect to a cut, allow the domain for ф to be reduced to a sector 0 < Z < n/p.
The boundary conditions are
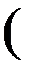
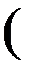 ф = 0 at Z = 0, £ > 1
ф = 0 at Z = 0, £ > 1
ф = 0 at Z = п/p, £ > 1
The circulation is calculated as in the lifting line problem assuming that the airfoil section £ of the blade has the same properties as that of infinite aspect ratio with a wind velocity vW+W, at an effective angle of attack (a – 6a), where a is the geometric angle of attack and 6a is the induced angle.
Imposing the periodicity condition is of interest also in the study of cascade problems.
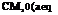
 x
x











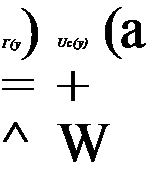
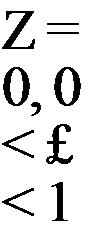

![Д дф д дф дх р'дх + дг '&quot;Hr = 0 &nbsp; (13.61) &nbsp; and &nbsp; д Щ - + д = 0 дх рг дх дг рг дг &nbsp; (13.62) &nbsp; These equations can be compared to the equations governing the electrical po­tential in a conducting medium of varying thickness. The depth of the conducting material will be proportional or inversely proportional to рг, depending on whether ф or ф is simulated. In the first case, inclined tank can be used to simulate flow around streamlined bodies of revolution, convergent wind tunnel ducts and axially symmet­ric air intakes. For the representation of the stream function, a tank with hyperbolic bottom can be constructed where the depth varies as 1/y, see Ref. [12]. &nbsp; 13.3.3 Hodograph Tank &nbsp; In the hodograph plane, the velocity potential ф and the stream function ф, of com­pressible fluid flow are related by the following equations &nbsp; д 1 дф д ( р дф дд ррд (1 - M2) дд + дв р0д дв ° &nbsp; (13.65) &nbsp; and &nbsp; (13.66) &nbsp Д дф д дф дх р'дх + дг '&quot;Hr = 0 &nbsp; (13.61) &nbsp; and &nbsp; д Щ - + д = 0 дх рг дх дг рг дг &nbsp; (13.62) &nbsp; These equations can be compared to the equations governing the electrical po­tential in a conducting medium of varying thickness. The depth of the conducting material will be proportional or inversely proportional to рг, depending on whether ф or ф is simulated. In the first case, inclined tank can be used to simulate flow around streamlined bodies of revolution, convergent wind tunnel ducts and axially symmet­ric air intakes. For the representation of the stream function, a tank with hyperbolic bottom can be constructed where the depth varies as 1/y, see Ref. [12]. &nbsp; 13.3.3 Hodograph Tank &nbsp; In the hodograph plane, the velocity potential ф and the stream function ф, of com­pressible fluid flow are related by the following equations &nbsp; д 1 дф д ( р дф дд ррд (1 - M2) дд + дв р0д дв ° &nbsp; (13.65) &nbsp; and &nbsp; (13.66) &nbsp](/img/3129/image1845.png)