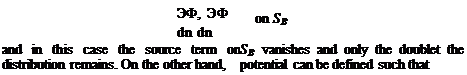The mathematical problem of the previous section is described schematically by Fig. 3.1. Laplace’s equation for the velocity potential must be solved for an arbitrary body with boundary SB enclosed in a volume V, with the outer boundary S„. The boundary conditions in Eqs. (3.2) and (3.3) apply to SB and Soo, respectively. The normal n is defined such that it always points outside the region of interest V. Now, the vector appearing in the divergence theorem (e. g., q in Eq. (1.20)) is replaced by the vector Ф^Ф2 — Фг^Фъ where Ф! and Ф2 are two scalar functions of position. This results in
(Ф^Ф2 – Ф2УФі). n dS = (Ф^2Ф2 – Ф^ФО dV (3.4)
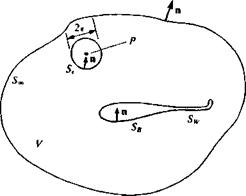 Nomenclature used to define the potential flow problem.
Nomenclature used to define the potential flow problem.
This equation is one of Green’s identities (Kellogg,13 p. 215). Here the surface integral is taken over all the boundaries S, including a wake model Sw (which might model a surface across which a discontinuity in the velocity potential or the velocity may occur).
 Фі = — and Ф2 = Ф r
Фі = — and Ф2 = Ф r
where Ф is the potential of the flow of interest in V, and r is the distance from a point P(x, y, z), as shown in the figure. As we shall see later, Ф, is the potential of a source (or sink) and is unbounded (1 /r—»») as P is approached and r-* 0. In the case where the point P is outside of V both Ф! and Ф2 satisfy Laplace’s equation and Eq. (3.4) becomes
I (lv<P-<l>vlyndS = 0 … (3.6)
Of particular interest is the case when the point P is inside the region. The point P must now be excluded from the region of integration and it is surrounded by a small sphere of radius e. Outside of the sphere and in the remaining region V the potential Ф! satisfies Laplace’s equation [V2(l/r) = 0]. Similarly У2Ф2 = 0 and Eq. (3.4) becomes
f (-V<P-<PV-)-ndS = 0 (3.6a)
To evaluate the integral over the sphere, introduce a spherical coordinate system at P and since the vector n points inside the small sphere, n = —er, n • УФ = — дФ/Эг and V(l/r) = —(l/r2)er. Equation (3.6a) now becomes
On the sphere surrounding P, J dS = Але2 (where r = e), and as e—>0 (and assuming that the potential and its derivatives are well-behaved functions and therefore do not vary much in the small sphere) the first term in the first integral vanishes, while the second term yields
-1 (?) dS = ~4лф(р)
«^sphere € ‘* ‘
Equation (3.66) then becomes
Ф(Р)=Т~ f (-УФ-ФУ-)-ndS (3.7)
4л Js r r)
This formula gives the value of Ф(Р) at any point in the flow, within the region V, in terms of the values of Ф and дФ/дп on the boundaries S.
If, for example, the point P lies on the boundary SB then in order to exclude the point from V, the integration is carried out only around the surrounding hemisphere (submerged in V) with radius e and Eq. (3.7) becomes
Ф(Р) = ^| 0уФ-ФУ^-ш<И (3.7a)
Now consider a situation when the flow of interest occurs inside the boundary of SB and the resulting “internal potential” is Ф,. For this flow the point P (which is in the region V) is exterior to SB and applying Eq. (3.6) yields
0 = – i-f (іуФ,-Ф, У-)-«^ "" (3.7b)
4л }Sb r г/
Here, n points outward from SB. A form of Eq. (3.7) that includes the influence of the inner potential, as well, is obtained by adding Eqs (3.7) and (3.7b) (note that the minus sign is a result of the opposite direction of n for
Ф,):
Ф(Р) = f Г – У(Ф — Ф,-) — (Ф — Ф<) V -1 • n dS 4я Jsgl/’ rJ
+ -— f (- 7Ф — Ф V -) • n dS (3.8)
4л JSw+Sw r rJ
The contribution of the integral in Eq. (3.8) (when S„ is considered to be far from SB) can be defined as ФХ(Р).
Ф.(Р) = —f (^Ф-ФУ-)-пгі5 (3.9)
4л Js. r r!
This potential, usually, depends on the selection of the coordinate system and, for example, in an inertial system where the body moves through an otherwise stationary fluid Ф® can be selected as a constant in the region. Also, the wake surface is assumed to be thin, such that ЭФ/дп is continuous across it (which means that no fluid-dynamic loads will be supported by the wake). With these assumptions Eq. (3.8) becomes
ф(Р) = —f ГІу(Ф-ФІ)-(Ф-Фі)У-1-п</5–^-f Фп • V – dS + Ф»(Р) v 4л JSb Lr r J 4л JSw r
(3.10)
As was stated before, Eq. (3.7) (or Eq. (3.10)) provides the value of Ф(Р) in terms of Ф and дФ/дп on the boundaries. Therefore, the problem is reduced to determining the value of these quantities on the boundaries. For example, consider a segment of the boundary SB as shown in Fig. 3.2; then the difference between the external and internal potentials can be defined as
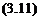 – jU = Ф – Ф,
– jU = Ф – Ф,
FIGURE 3.2
The velocity potential near a solid boundary Sb.
and the difference between the normal derivative of the external and internal potentials as
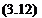
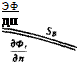
ЭФ ЭФ, dn dn
These elements are called doublet (/i) and source (o) and the minus sign is a result of the normal vector n pointing into SB. The properties of these elementary solutions will be investigated in the following sections. With the definitions of Eqs. (3.11) and (3.12), Eq. (3.10) can be rewritten as
(3.13)
The vector n here is the local normal to the surface, which points in the doublet direction (as will be shown in Section 3.5). It is convenient to replace n • V by d/dn in this equation, and it becomes
(3.13a)
Note that both source and doublet solutions decay as r-*°° and automatically fulfill the boundary condition of Eq. (3.3).
In order to find the velocity potential in the region V, the strength of the distribution of doublets and sources on the surface must be determined. Also, Eq. (3.13) does not specify a unique combination of sources and doublets for a particular problem and a choice must be made in this matter (usually based on the physics of the problem).
It is possible to require that
Ф, = Ф on SB
and in this case the doublet term on SB vanishes and the problem will be modeled by a source distribution on the boundary.
In the two-dimensional case the source potential is «I»! = In r as will be shown in Section 3.7, and the two functions of Eq. (3.5) become
Фі = In r and Ф2 = Ф (3.14)
Also at the point P, the integration is around a circle with radius є and Eq.
(3.66) becomes
— f (in r ^ — Ф -) dS + f (In г УФ – ФУ In r) • n dS = 0 (3.15)
•’circle € ‘ v/" Г / J5
The circumference of the small circle around P is now 2лє (compared to 4;re2 in the three-dimensional case) and Eq. (3.7) in two dimensions is
Ф(Р) = -2- f (In г УФ – Ф V In r) • n dS (3.16)
2 Jt J5
If the point P lies on the boundary SB, then the integration is around a semicircle with radius є and Eq. (3.16) becomes
Ф(Р)=– f (lnrV<P-<PVlnr)-ndS (3.16a)
Л Js
whereas if P is inside SB the two-dimensional version of Eq. (3.76) is
0 = — t— f (In г УФ, — Ф, V In r) • n dS (3.166)
2 л Js
With the definition of the far field potential Ф» and the unit elements fi and a being unchanged, Eq. (3.13a) for the two-dimensional case becomes
ф(/,) ■ h l. [°1to ■r ^~ ■ці(to ■r)] ■- h 1 -‘‘inV"r)i^ф-(п (3-‘‘7)
Note that d/dn is the orientation of the doublet as will be illustrated in Section
3.7 and that the wake model Sw in the steady, two-dimensional lifting case is needed to represent a discontinuity in the potential Ф.
 W = — = — -—:———ї ~ :———— гт“—5 (3.90)
W = — = — -—:———ї ~ :———— гт“—5 (3.90)
![]() (3.91)
(3.91)










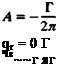
 __3W______
__3W______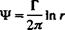 (3.85)
(3.85)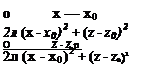
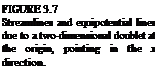
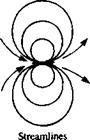
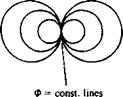

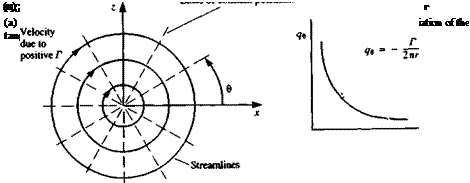
 FIGURE 3.4
FIGURE 3.4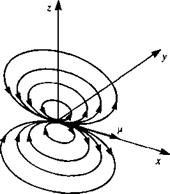 Sketch of the streamlines due to a doublet pointing in the x direction (e. g., like a small jet engine blowing in the ц = (ft, 0, 0) direction).
Sketch of the streamlines due to a doublet pointing in the x direction (e. g., like a small jet engine blowing in the ц = (ft, 0, 0) direction).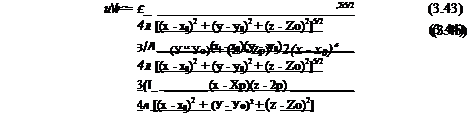
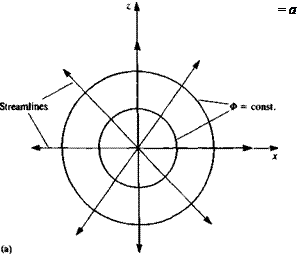
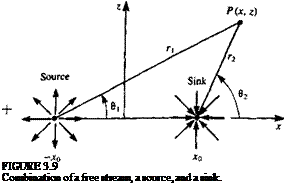
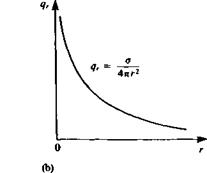 FIGURE 33
FIGURE 33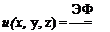
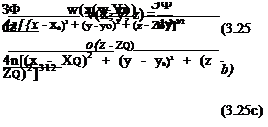

 Nomenclature used to define the potential flow problem.
Nomenclature used to define the potential flow problem.