Really ingenious nonelectronic stability augmentation systems came out of the jet’s awkward age, as designers tried to have artificial damping without the heavy, costly, and, above all, unreliable electronics of the period. A mechanical yaw damper, invented by Roland J. White and installed on early Boeing B-52 Stratofortresses, is a good example of the genre.
Imagine a rudder tab that is free to rotate on low friction bearings. Instead of being connected to an electric actuator, or to cables leading to the cockpit, the free tab is driven by
|
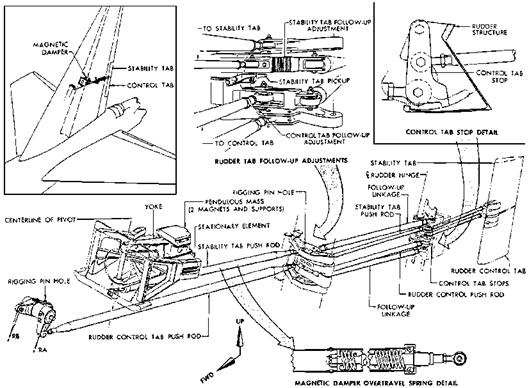
Figure 7.1 Boeing B-52 rudder control linkages. R. J. White’s magnetically phased bobweight yaw damper operates the stability tab. (From B-52 Training Manual, 1956)
|
inertia forces acting on a small bobweight located ahead of the hinge line (Figure 7.1). Tab position is further modified dynamically by an eddy current damper, providing damping hinge moments proportional to tab rotational velocity.
As the airplane goes through a typical lateral or Dutch roll oscillation, the vertical tail assembly swings from side to side, accelerating the tab bobweight. Without the eddy current damper it is clear that the tab will take up deflections in phase with the lateral acceleration at the vertical tail. However, ideally, tab positions should be phased with respect to yawing velocity in such a way as to drive the rudder in opposition. This is the classic yaw damping action, right rudder in opposition to left yawing velocity. The function of the eddy current damper is to “tune” tab deflections to create exactly that phasing. In 1952, a similar approach was taken by M. J. Abzug and Hans C. Vetter of the A3D Skywarrior design team at Douglas Aircraft, to provide nonelectronic yaw damping for that airplane. The design method was cut and try on the analog computer, to find the proper combination of bobweight mass and damper size that would phase the tab, creating effective yaw damping.
The obvious practical problem with the B-52 and A3D yaw dampers is one that is faced with any purely mechanical system, as compared with a modern electromechanical control system. In the mechanical system, the result or output depends critically on the condition of each component. If the free tab’s bearings deteriorate over time or are invaded by grit, or if the eddy current damper’s effectiveness is changed, tab phasing will be thrown off.
In the extreme case, tab action could actually add to the airplane’s lateral oscillation, instead of damping it.
In a July 1994 letter Roland White describes such a situation that actually occurred on a B-52, as follows:
A rudder tail shake on a test airplane caused the magnetic damper to lose its damping. A serious accident would have occurred if the bobweight did not jam due to a mechanical failure. After that I found when going to work the next day your friends will ask if you still work here.
A modern, electromechanical yaw damper drives the rudder in opposition to the measured rate of yaw. It does so by comparing the current rudder position with the desired value and continuing to exert torque on the rudder until that value is reached, overriding mechanical obstacles such as sticky bearings or even losses in performance of the motor that drives the rudder.
The practical shortcomings of purely mechanical yaw damping were not unknown to the Boeing and Douglas design staffs. When a chance appeared to get a yaw damper function electronically, that option was taken instead. In the case of the B-52, the spring-tab – controlled rudders were replaced by powered rudders, allowing Boeing to use the electromechanical yaw damper design developed successfully for the B-47.
In the Douglas case, electromechanical yaw damping was installed using components of the airplane’s well-proved Sperry A-12 automatic pilot. The Sperry Gyroscope Company’s DC-3 “dogship” proved the concept in test flights at the Sperry plant in Long Island, New York. Signals from the outer, or yaw, gimbal of the A-12’s free directional gyro were electronically differentiated through a lead network and sent to the rudder servo. Differentiated yaw angle is of course yaw rate.
This worked well when the system was transferred to the A3D and flown routinely at Edwards Air Force Base. Then one day a test pilot bringing an A3D back for landing dove at the runway and pulled up into a chandelle, a natural thing to do for a high-spirited test pilot with an airplane he likes. The A3D, with yaw damper on, responded by applying bottom rudder during the nearly vertical bank, diving the ship back toward the ground.
The pilot regained control and an investigation started at once. The A-12 and yaw damper function were found to be in perfect order. The culprit turned out to be what had been called for years “gimbal error.” The A-12 directional gyro is a conventional two-gimbal free gyro, with yaw measured on the outer gimbal. The rotor, spinning in the inner gimbal, is slaved to magnetic north and the inner gimbal itself is erected to gravity by a bubble level system. The angle between the outer gimbal and the instrument’s case is true yaw or heading angle as long as the outer and inner gimbals are at right angles to each other. This holds only for zero bank angle. At the sharp bank angles of the chandelle, or in any steep turn, the yaw reading picks up errors that depend on the heading angle (Figure 7.2).
During turns, differentiation with respect to time of the erroneous yaw angle exaggerates the ordinary gimbal errors. The A3D experience proves dramatically that one cannot in general differentiate free gyro signals to produce damping signals for stability augmentation, at least for airplanes that maneuver radically. After the all-mechanical and free-gyro A3D yaw damper designs were proved faulty the airplane was finally fitted with what is now the standard design, a single-degree-of-freedom yaw rate gyro driving the rudder servo.
A rather more successful nonelectronic stability augmentation system was developed at the Naval Weapons Center, China Lake, for the AIM-9 Sidewinder missile. The Sidewinder
|
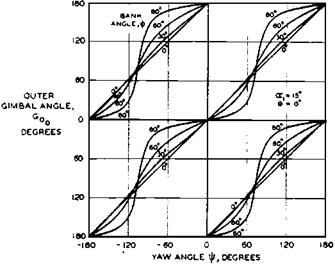
Figure 7.2 Gimbal angles of the outer gimbal of the Sperry A-12 directional gyro, as a function of bank and yaw angles. The outer gimbal rate fluctuates strongly in turns at steep bank angles. Differentiating outer gimbal angle to obtain yaw rate caused a near-crash of a Douglas A3D-1 Sky Warrior. (From Abzug, Jour. of the Aero. Sciences, July 1956)
|
derives roll damping from nonelectronic, air-driven flywheels mounted at the tips of the missile’s ailerons, producing gyroscopic torques that drive the ailerons to oppose roll rate. The flywheel torques are evidently high enough to override variations in aileron bearing friction. There seems to have been no application of this all-mechanical damping system to airplanes.