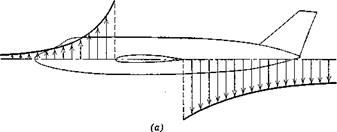
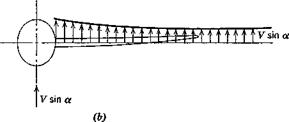
On summing (6.3,4) and (6.3,12) and adding the contribution G^ for the propulsive system, we obtain the total pitching moment about the C. G.,
0» – ^a. e.rt + (cLwb + oLl I) (h – KJ – VHCLi + Cmv
(6.3,13)
Since CL is a coefficient based on 8t, then GL8tf8 is the tail contribution to CL, and the total lift coefficient of the vehicle is
Cl = C^ + (6.3,14)
Equation (6.3,13) therefore becomes
= ^a. e.ttS + – KJ – rHCLt + cmf (6.3,15)
It is worthwhile repeating that no assumptions about thrust, compressibility, or aeroelastic effects have been made in respect of (6.3,15). The pitch stiffness (—C ) is now obtained from (6.3,15). Recall that the aerodynamic centers of the wing-body combination and of the tail are fixed points, so that
C^ = + cLx(h – KJ – vHd-^ + ^ (6.3,16)
If a true aerodynamic center in the classical sense exists, then dO ^ Jda. is zero and
do, dcm
= Cu(h – KJ – Vh-£ + (6.3,17)
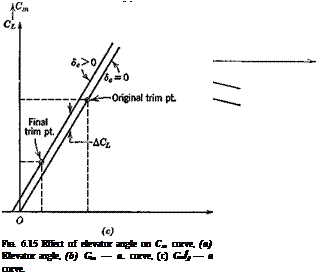
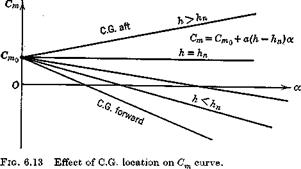
Cm^ as given by (6.3,16) or (6.3,17) is a constant that depends linearly on the C. G. position, h. Since CL^ is usually large, the magnitude and sign of Gm^ depend strongly on h. This is the, basis of the statement in Sec. 6.2 that C can always be made negative by a suitable choice of h. The C. G. position hn for which Gm is zero is of particular significance, since this represents a boundary between positive and negative pitch stiffness. In this book we define hn as the neutral point, N. P. It has the same significance for the vehicle as a whole as does the aerodynamic center for a wing alone, and indeed the term vehicle aerodynamic center is an acceptable alternative to “neutral point.”
The location of the N. P. is readily calculated from (6.3,16), i. e.
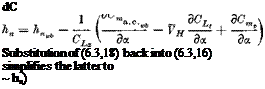 (6.3,18)
(6.3,18)
(6.3,19) which is valid whether Gma c and Cm^ vary with a or not. Equation (6.3,19) clearly provides an excellent way of finding hn from test results, i. e. from measurements of Cm and CL. The difference between the C. G. position and the N. P. is sometimes called the static margin,
 Kn = (K – h)
Kn = (K – h)
Since the criterion to be satisfied is C < 0, i. e. positive pitch stiffness, then we see that we must have h < hn, or Kn > 0. In other words the C. G. must be forward of the N. P. The farther forward the C. G. the greater is Kn, and in the sense of “static stability” the more stable the vehicle.
It must be emphasized that Gm and Gare partial derivatives. This means that all other significant arguments, normally M, CT, and p V2 are kept constant. This is especially important to keep in mind when experimental results are being used. If these parameters are unimportant or absent, as in the gliding flight of a rigid vehicle at low M, then Gm and 0L are functions of к only, Gm is a unique function of CL, and (6.3,19) yields
 (6.3,21)
(6.3,21)
Equation (6.3,21) is sometimes used in practice as a definition of the neutral point, but as is clear from the foregoing, it contains some dangers. Since Gm and CL are in the general case each functions of several independent variables, then the derivative dCmjdCL is not mathematically defined, and indeed different values for it can be calculated depending on what constraints are imposed on the independent variables. With particular constraints it indeed turns out to be a useful index of stability, and this point is treated further in Sec. 9.3.
![]() Чее = °T^ + °L^e ^“free = ^mS^etree
Чее = °T^ + °L^e ^“free = ^mS^etree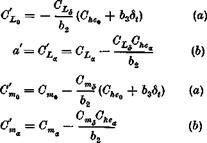











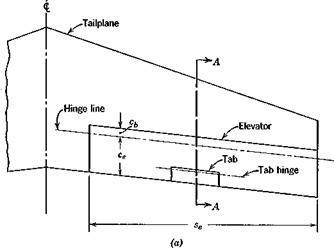
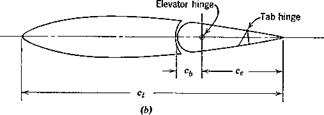
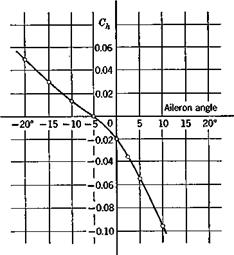

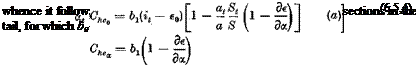


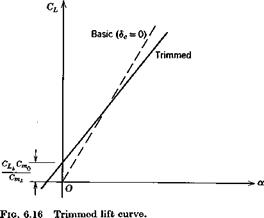



 of the zero-lift line of the whole configuration (see Fig. 6.12). Note that, since it is negative, then (CL)0 is negative. The difference between a and awb is found by equating (6.3,296 and c) to be
of the zero-lift line of the whole configuration (see Fig. 6.12). Note that, since it is negative, then (CL)0 is negative. The difference between a and awb is found by equating (6.3,296 and c) to be Cm = + Gift1 ~ K)
Cm = + Gift1 ~ K)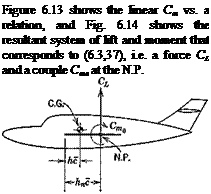
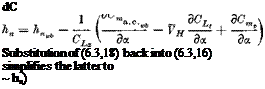 (6.3,18)
(6.3,18)