Category Dynamics of. Atmospheric Flight

Let the cubic equation be

,4s3 + Bs2 + Cs + D = 0 (A > 0)

Then

F0 = A, F1 = B, F2 = BC – AD, F3 = D(BG – AD)

The necessary and sufficient conditions for all the test functions to be positive are that A, B, D, and (BG — AD) be positive. It follows that G also must be positive.

TEST FUNCTIONS FOR A QUARTIC

Let the quartic equation be

As4 + Bs3 + Cs2 + Ds + E = 0 {A > 0)

Then the test functions are F0 = A, F1 = B, F2 = BG — AD, F3 — F2D — B2E, F4 = FSBE. The necessary and sufficient conditions for these test functions to be positive are

A, B,D, E> 0

and D{BC – AD) – B2E > 0 (3.3,50)

It follows that C also must be positive. The quantity on the left-hand side of (3.3,50) is commonly known as Bouth’s discriminant.

TEST FUNCTIONS FOR A QUINTIC

Let the quintic equation be

As5 + Bs4 + Cs3 + Ds2 + Es + F = 0 (A > 0)

Then the test functions are F0 = A, Fx = B, F2 — BG — AD, F3 = F2D – B(BE – AF), Ft = F3(BE – AF) – F2F, F& = FtF2F. These test functions will all be positive provided that

A, B, D, F, F2, Ft > 0

It follows that C and E also are necessarily positive.

COMPLEX CHARACTERISTIC EQUATION

There may arise certain situations in which some of the coefficients of the differential equations of the system are complex instead of real, and conse­quently some of the coefficients of the characteristic equation are complex too. The criteria for stability in that case are discussed by Morris (ref. 3.7).

As noted in the foregoing, the stability of a linear/invariant system is determined by the roots of the characteristic equation. A characteristic mode will be divergent if its real part is positive, and. convergent if the real part is negative, the latter denoting asymptotic stability. It is not necessary, however, actually to solve the characteristic equation in order to find whether the roots have positive real parts. This can be determined from its coefficients alone. The conditions on the coefficients that must be satisfied were first stated by Routh (ref. 3.5), who derived them from a theorem of Cauchy. Let the characteristic equation be

<Vn + W*"1 + • ■ • + c0 = 0 (e. > 0) (3.3,55)

The coefficient cn can always be made positive by changing signs throughout, so the requirement cn > 0 is not restrictive. The necessary and sufficient condition for asymptotic stability (i. e. that no root of the equation shall be zero or have a positive real part) is that each of a series of test functions shall be positive. The test functions are constructed by the simple scheme shown below. Write the coefficients of (3.3,55) in two rows as follows:

n vn-2 °n-4

Cn-1 CM-3 CM-5 ‘ ‘ ‘

Mow construct additional rows by cross-multiplication:

P*. Р32 P33 * ‘ *

P41 P42 P43 ‘ ‘ ’

51

etc.

where

P31 = Cn-lCn-2 ~~ cncn-З’ Р32 = Cn-lcn-4 cncn-5> e^c-

and

Р41 = РзіСп-3 Рз2Сп-1> P42 = Р’ЯСп-5 Cn-1^33’ e^°’

Р51 = ^44^32 Р? лРцг ef°-

The required test functions F0 • ■ ■ Fn are then the elements of the first column, cn, cn_v Pm ■ ■ • Pm+lil. If they are all positive, then there are no unstable roots. The number of test functions is n + 1, and the last one, Fn, always contains the product c0Fn_1. Duncan (ref. 3.6, Sec. 4.10) has shown that the vanishing of c0 and of Fn_x represent significant critical cases. If the system is stable, and some design parameter is then varied in such a way as to lead to instability, then the following conditions hold:

(a) If only c0 changes from + to —, then one real root changes from negative to positive; i. e. one divergence appears in the solution (Fig. 3.6).

(b) If only Fn_x changes from + to —, then the real part of one complex pair of roots changes from negative to positive; i. e. one divergent oscillation appears in the solution (Fig. 3.6).

Thus the conditions c0 = 0 and Fn_^ = 0 define boundaries between stability and instability. The former is the boundary between stability and static instability, and the latter is the boundary between stability and a divergent oscillation.

In this section we show how the given system of simultaneous, or coupled, real differential equations can be transformed into a new set of separate or uncoupled equations, one for each of the new variables. This decoupling is produced by in effect selecting the eigenvectors as the coordinate system for the state space instead of the original coordinates, the yt.

Let the n X n matrix formed of the n eigenvectors be

U = [Ulu2 • • • uj (3.3,38)

Now let us define a new set of system variables (state space coordinates) q( by the transformation

y = Uq; q = U^y (3.3,39)

(Recall that for self-adjoint systems, U is an orthogonal matrix and U7′ = U-1; the above transformation is then orthogonal. In general, however, this is not the case.) It follows from (3.3,39) that

y(«) = 2 u M*) (3.3,40)

i=1

i. e. that the state vector is a superposition of n vectors parallel to the eigen­vectors. The qft) are the characteristic coordinates. Comparison with (3.3,10) shows that they must be of the form oqe*** where oq are arbitrary constants. Substitution of (3.3,39) into the differential equation of the system, (3.3,1) then yields

Uq = AUq

or, premultiplying by U_1,

q = U_1AUq (3.3,41)

We must now examine the matrix THAU. Using (3.3,38) we have AU = A[ujU2 • • • u J = [AujAu2 • • • Au„]

But the defining condition on the eigenvectors is

where, as can be verified by direct expansion, exp Лі gives the diagonal matrix of the exponential coefficients. Comparison of (3.3,49) with (3.3,13) shows that

eAl = Ue^U-1 (3.3,50)

The usual situation in vehicle dynamics is that some of the eigenvalues and eigenvectors occur in conjugate complex pairs. Thus some members of (3.3,46) will correspondingly be complex pairs. These may be transformed into a set of second-order equations, one for each complex pair of qt. Thus let qs and qj+l = q* be such a pair. The corresponding equations are

The oq and /3,- are now real linear combinations of the original variables yt that can be calculated by expanding (3.3,39). The pair of conjugate equations are now expanded by means of (3.3,52) to give

<*i + = K – + + *&)

= К — – tfi)

Taking real and imaginary parts of either of the above leads to the alternative pair of first-order coupled equations

&j = «,■(*,■ — co,/3,-

Д,- = oj/j. j + rijfij (3.3,53)

Finally, by eliminating oq or /3,- we get a pair of uncoupled real second-order equations

oq — 2nd.) + (та2 + co2)cq = 0

/З,- – 2+ (та2 + «и2)/?, = 0 (3.3,54)

These equations for the a, /5 replace the original pair of complex first-order equations (3.3,51). However, the number of arbitrary constants in the solutions of (3.3,54) is still only two, i. e. cq(0) and /3,(0), since (3.3,53) fix the inital values of oq and

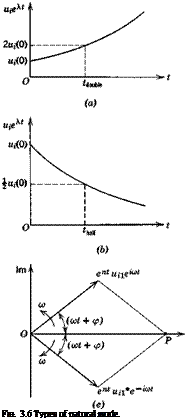
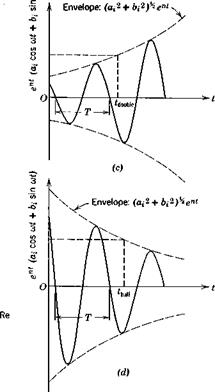
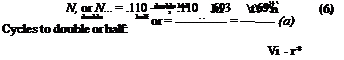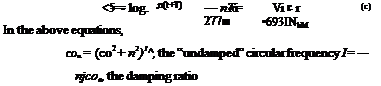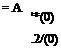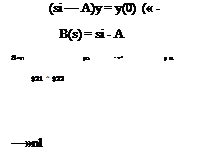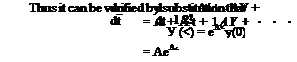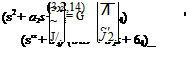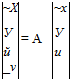Solutions of the kind given by (3.3,14) describe special simple motions called natural modes or simply modes of the system. If the eigenvectors are orthogonal, the modes are normal or orthogonal modes. When A is real, the modes are exponential in form, as in Fig. 3.6a and 6—increasing in magni­tude for A positive, and diminishing for A negative. Thus A < 0 corresponds to stability, usually termed static stability in the aerospace vehicle context, and A > 0 corresponds to static instability, or divergence. The times to double or half of the starting value illustrated in the figure are given by

When one Ar is complex, for real matrices A, there is always a second that is its conjugate, and the conjugate pair, denoted (letting r = 1,2)

Aj,2 = П і І<0

define an oscillatory mode of period T = 2 tt/cd as we shall now show. The sum of the two particular solutions (3.3,14) corresponding to the complex pair of roots is

у = Ule(B+i0,)< + и2е(я-іш)<

where Uj and u2 are the eigenvectors for the two A’s. On factoring out ent we get

у = епі(щеіаі + и2е-іші) (3.3,26)

If the elements of the system matrix A are real, then the corresponding elements of Uj and u2 always turn out to be conjugate complex pairs, i. e.

u2 = uf

64 Dynamics of atmospheric flight and (3.3,26) becomes

у = eni(a cos cot + b sin cot) (3.3,27)

where a = Uj + uf and b = «(Uj — uj) are real vectors. Equation (3.3,27) describes, for any particular state variable yt, an oscillatory variation that increases if n > 0 (dynamic instability, or divergent oscillation) and decreases (damped oscillation) if n < 0—see Fig. 3.6c and d. The initial condition corresponding to (3.3,27) is

y(0) = a = ux + uf (3.3,28)

With reference to Fig. 3.6c and d, some useful measures of the rate of growth or decay of the oscillation are:

Time to double or half:

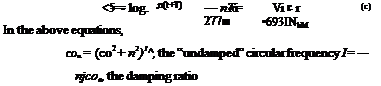
Logarithmic decrement (log of ratio of successive peaks):

One significance of the eigenvectors is seen to be that they determine the relative values of the state variables (the “direction” of the state vector in state space) in a characteristic mode. If the mode is nonperiodic, the eigen­vector defines a fixed line through the origin in state space, and the motion in the mode is given by that of a point moving exponently along this line. If the mode is oscillatory, the state vector is given by (3.3,27), and the locus of у is clearly a plane figure in the (a, b) plane through the origin. If n = 0, it is an ellipse, otherwise it is an increasing or decreasing elliptic spiral. The vectors a and b are twice the real and imaginary parts respectively of the complex eigenvector associated with the mode. It should be emphasized that these modes are special simple motions of the system that can occur if

the initial conditions are correctly chosen. In them all the variables change together in the same manner, i. e. have the same frequency and rate of growth or decay. It is instructive to consider the Argand diagram corresponding to (3.3,26). For any component y. L we have

y. = ent(uaei<oi + u*e-iat) (3.3,30)

which is depicted graphically in Fig. 3.6e, where ua = ua ё’ср. The two vectors are conjugate, i. e. symmetric w. r.t. the real axis, and rotate in opposite directions with angular speed w. The real value y^t) is given by their sum, the vector OP. As they rotate, the two vectors shrink or grow in length, according to the sign of n.

Once again it is necessary to consider separately the ease of repeated roots. Let us treat specifically the double root, i. e. m = 2 in (2.5,7). Then (3.3,14) is no longer the appropriate particular solution. Instead, we get from (2.5,7) a particular solution of the form

у (t) = ureV + vrte^f (3.3,31)

where ur and vr are constant vectors, ur being the initial state ur = y(0). On substituting (3.3,31) into (3.3,1), and dividing out eM, we find

{Xrur + vr) + Xrvrt = Aur + Av, f (3.3,32)

Since this must hold for all t, we may set t = 0, obtaining

(Arur + vr) = Aur

or vr = (A — ArI)ur

= —B(A>r Ф)

where В is given by (3.3,3), and (3.3,31) becomes

У(t) = (I – B(Ar)<)ureV (3.3,34)

After substituting (3.3,33a) in (3.3,32) a second relation is obtained, i. e.

Equation (3.3,31) will be a solution of (3.3,1) as assumed, if there exist a Xr and a vr that satisfy (3.3,35), and if ur given by (3.3,335) is not infinite. The first of these conditions requires that the original characteristic equation be satisfied, i. e.

It will now, because of the double root, be of the form

№ = (A – KfgW = 0 g(K) ф о (3.3,36)

and this condition is of course satisfied. The second condition is met by any eigenvalues found as described previously for repeated roots. Finally, the value of ur can be shown to be given by

= (-£ Т(ЯА (3-3,37)

dl ]x=xr

where v(A) is the column of adj В that gives the eigenvector vr.

When the procedure given in the foregoing is applied to calculate eigen­vectors for cases of multiple roots of the characteristic equation, additional possibilities occur. (See refs. 3.3 and 2.2.) Let the multiple root occur at

« = X„

(i) If adj B(XB) is not a null matrix, then its nonzero columns give a single eigenvector, just as for distinct eigenvalues. In that case there is only one eigenvector for the multiple root.

(ii) If adj В(Я„) is null, and its first derivative djds adj B(s)|s=A]> is not, then there are two linearly independent columns of the latter that give two independent eigenvectors.

(iii) If the first derivative is also null, then higher derivatives will yield successively larger numbers of eigenvectors.

EQUATIONS IN NONSTANDARD FORM

It is not necessary, nor always more convenient, to work with the system equations in standard first-order form, as was done above. The characteristic equation can be found directly from the equations as they are initially formulated, the “natural” form. Consider (3.2,10) for example. The autono­mous equations are

(3.3,21)

Assume there is an eigenfunction solution like (3.3,14), i. e.

(3.3,23)

The square matrix of (3.3,23) is exactly the same as В in (3.2,13), A replacing s. Since (3.3,23) are homogeneous equations the determinant of В must be zero. Expanding it leads exactly to the correct characteristic equation, just as would be obtained from the standard first-order form. Equation (3.3,23) is of the same form as (3.3,156) and the same argument for finding an eigenvector applies—i. e. a column (z(O), y(0)) that satisfies (3.3,23) is any non vanishing column of adj B. To complete the eigenvector we need x(0) and 2/(0). These are simply, from (3.3,22),

where A is the appropriate eigenvalue.

For low-order systems, the characteristic determinant can be directly expanded and the characteristic equation (3.3,7) written out. If n < 4, analytical solutions exist for the roots. For large-order systems the eigen­values and eigenvectors are computed from the system matrix A by digital machine methods (refs. 3.3, 3.4). A discussion of these methods and of their recommended spheres of application is beyond the scope of this volume. Suffice it to say that practical methods and computing routines are available in most computation centers for extracting the eigenvalues and eigenvectors for systems of very large order, even for n > 100.

It is worthwhile describing one fairly direct approach to computation of eigenvectors. Consider (3.3,156) as a homogeneous set of scalar equations with lr known and the n components of ur as the unknowns. Now divide through all the equations by any one of the unknowns, say umr, so that there results n equations for (n — 1) ratios и{г/итг. By dropping any one of the equations and transposing the coefficients of umT to the r. h.s., a complete set of (n — 1) equations is obtained for the (n — 1) ratios. These can be solved by any conventional method to yield the ratios of all the components of ufto umr. The equations will of course have complex coefficients for complex eigen­values, and real coefficients for real eigenvalues. This process for a third – order system would go as follows:

bn(kr)ulr + b12(?ir)u2r + b13(kr)u3r = 0

b21(Xr)ulr + b33(Xr)w3r +

^2з(^г)м3г — 0 hl(K)Ulr + bai(K)U2r + b3z(K)U3r = 0

After dividing by u3r and dropping the third equation we get

h – Її °n —

%3r

b21^ + b2

The solution of this set of equations gives the two required ratios in terms of which the eigenvector is [м1г/м3г, 1]. There are two difficulties

associated with this method. The first is that if u3r turns out to be very small relative to ulT and u2r the equations will be ill-conditioned, and a different choice for the component to divide by has to be made. The second is that when X is complex, there are really two sets of equations to be solved for the real and imaginary parts of the ratios.

Clearly the eigenvector corresponding to the conjugate eigenvalue X* will be itself the conjugate of ur, so only one of the pair need be calculated.

When the matrix A is symmetric (not, unfortunately, a common occurrence in the equations of flight vehicles) the system is called self-adjoint, and the eigenvectors have the convenient special property of being orthogonal, or normal. That is, the scalar product of any vector with any other is zero, i. e.,

u TUi = u, • иг = 0 Іф j (3.3,20)

In more general cases, when the system is not self-adjoint, and A is an arbitrary n X n matrix, the eigenvectors are neither real nor orthogonal. However, there still exists a reciprocal basis of the eigenvectors, i. e. a set of n vectors Vj orthonormal to the set іц, i. e. such that

= [<У

Thus the matrix V of the vectors vt evidently satisfies the condition

VrU = I

and clearly YT = U_1

i. e. the columns of V are the rows of U-1. The question now naturally arises as to what system (the adjoint system) has vz – as its eigenvectors, and whether its matrix, В say, has any relation to A. It can be shown that (ref. 3.1) В = AT, i. e. that the matrix of the system adjoint to A is AT and its eigenvectors are orthogonal to those of A.

The roots Ar of the characteristic equations are known as eigenvalues, or characteristic values. Corresponding to each of them is a special set of initial conditions that lead to a specially simple solution in which only one term of (3.3,10) remains, i. e.

у (t) = игеЛг< (a)

where y(0) = ur (b) (3.3,14)

Since the solution of the autonomous system corresponding to a given set of initial conditions is unique, then if (3.3,14a) is a possible solution (and we shall show that it is), then (3.3,146) gives the unique set of initial con­ditions that produce it. The general solution (3.3,10) is seen to be a super­position of these special solutions. ur is the eigenvector corresponding to?.r, and (3.3,14a) is the associated eigenfunction. Substitution of (3.3,14) into (3.3,1) gives

f For a discussion of the practical computation of eM see Appendix D-8 of ref. 3.1.

Since the expansion of (3.3,15) is a set of homogeneous algebraic equations in the unknowns uir a nontrivial solution exists only if the determinant equals zero, i. e. if

|B(Ar)| = 0 (3.3,16)

However, the Xr are the roots of the characteristic equation |B(.s)| = 0, and hence the condition (3.3,16) is automatically met. The vectors ur are then any that satisfy (3.3,15). It should be noted that since the r. h.s. of (3.3,15) is zero, the multiplication of any eigenvector by a scalar produces another eigenvector that has the same “direction” but different magnitude. To find ur we observe that, from the definition of an inverse (3.3,5),

adj В = В-1 |В| (3.3,17)

Premultiplying by В yields

В adj В = ІВІІ = f(s)I (3.3,18)

For any eigenvalue Xr, we have f(Xr) = 0, and hence

B(Ar) adj B(Ar) = 0 (3.3,19)

Since the null matrix has all its columns zero, then it follows that each column of adj B(Ar) is a vector that satisfies (3.3,156). Hence any nonzero column of adj B(Ar) (if there are more than one, they differ only by constant factors) is an eigenvector corresponding to Xr. The eigenvalues and eigen­vectors are the most important properties of autonomous systems. From them one can deduce everything required about its performance and stability. This is illustrated in detail for flight vehicles in Chapter 9.

The n eigenvectors form the eigenmatrix

U = [utu2 • • • u„] = K,] in which ui} is the ith component of the jth vector.

The general equation for linear/invariant systems is (3.2,20). When the system is autonomous and hence has zero input it reduces to

У = Ay (3.3,1)

When the initial state vector is y(0), the Laplace transform of (3.3,1) is

sy = Ay + y(0)

in which atj are the elements of A. В is called the characteristic matrix of the system. Equation (3.3,2) then becomes

By virtue of the definition of the adjoint matrix (ref. 2.1) it is evident that the elements of adj В and of |B| are polynomials in s. |B| is called the char­acteristic determinant, and its expansion

|B| =/(e) (3.3,6)

is the characteristic polynomial. It is evident from (3.3,3) that /(s) is of the

nth degree. Hence

f(s) = sn + cn_1sn~’1 H——– c0

= (s – ^)(s -*,)•••(«- K) (3.3,7)

where • ).n are the roots of /(s) = 0, the characteristic equation. We now rewrite (3.3,4) as

l(s) = ~^-У(0) (3-3,8)

f(s)

The inversion theorem (2.5,6) can be applied to (3.3,8) for each element of y, and the column of these inverses is the inverse of y(s), i. e.

УV) = I P B(S)) y(0)eA,<

r=l l f(s) }s=xr

We now define the vector

and hence can write the general solution of (3.3,1) that satisfies the initial conditions as

. У« = І>е^ (3.3,10)

r~ 1

n

It follows that y(0) = 2 Уr Note also that by setting t = 0 in (3.3,9) the

r=l

summation therein is shown to be equal to the identity matrix I.

COMPACT FORM OF SOLUTION

A more compact form of the solution is available. Define the exponential function of a matrix M by an infinite series (like the ordinary exponential of a scalar), i. e.f

eM=I + M + – M2 + — –

2!

It is evident then that

is a solution of (3.3,1) that has the initial value y(0).

The transfer functions of a physical system that exists and is available for testing can be found from experiment, by making suitable measurements of its inputs and outputs. Here we are concerned with obtaining the transfer function by analysis. The experimental method is based in any case on the analytical formalism that we develop in the following. The procedure begins, of course, with the application of the appropriate physical laws that govern the behavior of the system. When the complete set of equations that express these laws has been formulated, it will, for linear/invariant systems, usually appear as a set of coupled differential equations of mixed order. A partic­ularly simple example (the second-order system) was given above, and it demonstrates what may be called the direct method of finding transfer functions. That is, form the Laplace transform of the system equations, just as they naturally occur, and solve for the appropriate ratios. We give a further illustration below for a pair of coupled second-order equations (a fourth-order system), such as might arise in the analysis of a double pendulum, or two massive particles on a stretched string, or two coupled L-R-C circuits, etc. The example equations are

* + «!# + «2* + a3x + a4 у = Л £ + Ky + b2y + b3x + bAy = /2

On forming the Laplace transforms, with

Ф) = 2/(0) = *(0) = 2/(0) = 0

the result is x(s2 + a2s + a3) + ^(cqs2 + a4) = f

z(s2 + b3) + i/(V2 + V + bi) = A

which can readily be solved for the four required transfer functions. We rewrite (3.2,12) as

(3.2,13)

(3.2,15)

is the matrix of the four transfer functions that relate x and у outputs to Д and /2 inputs. There are however two other state variables, making the required total of four, and consequently there are four more transfer functions to be found. The additional variables are the two rates

x = и y = v

The transforms of (3.2,16) with zero initial values are

sx = и sy = V

whence the four additional transfer functions are [see (3.2,3d)]

G^ = S=*d4=sG*fl <3-2’i7>

Ції vfi

and similarly

Gvf1 = sGvf1> Gv/2 = sGvf2

An alternative procedure for finding the matrix of system transfer functions consists of putting the equations in the standard first-order form. Any rtth- order system of linear equations can be expressed as a set of n first-order equations. Consider (3.2,10) for example. By using (3.2,16) they become

u + axv = a2u – a3x – a^y + Д ^

й + bji = — V — b3x — b4y + /a ’

which together with (3.2,16) are the required four first-order equations. They are not yet in the standard form, however. For that, one first solves (3.2,18) for и and v, which are linear functions of u, v, x, y, fv and/2. Combining the result with (3.2,16) yields a matrix equation of the form

where A is a 4 X 4 matrix, and C is a 4 x 2 matrix. (The determination of A and C is left as an exercise for the reader.)

Equation (3.2,19) is an example of the canonical form, which for the general linear system is

(3.2,20)

where у is the state и-vector and x the nonautonomous input r-vector. A (an n x n matrix) and C (an n x r matrix) may in general be time depend­ent. Here however, we are confining the discussion to invariant systems, and hence the Laplace transform of (3.2,20) is simply, for y(0) = 0

where I is the identity matrix. It follows that

у = («I – A)_1Cx (3.2,22)

From (3.2,36) we can therefore identify G as

G = (si – A)-*C

It can in principle be evaluated whenever A and C are known.