In the interest of completeness, the rigid-body equations are derived from first principles, that is to say, we apply Newton’s laws to an element dm of the airplane, and then integrate over all elements. The velocities and accelerations must of course be relative to an inertial, or Newtonian, frame of reference. As we noted in Sec. 1.6 the frame Fe, fixed to the Earth, is assumed to be such a frame. We also noted there that velocities relative to FE are identified by a superscript E. In order to avoid the carrying of the cumbersome superscript throughout the following development, we shall
temporarily assume that W = 0 in (1.6,1), so that Vе — V, and make an appropriate adjustment at the end. In the frame FB
VB = [u v w]r (4.2,1)
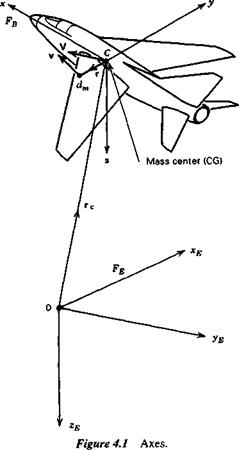
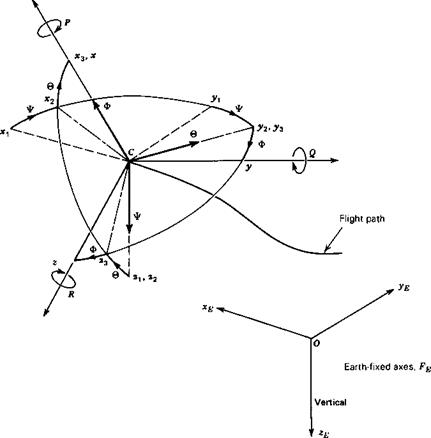
The position vector of dm relative to the origin of FE is rc + r (see Fig. 4.1). In the frame Fe,
r, f: = [xE Уе ZEf (4-2,2)
and in the frame FB
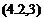
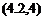
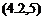 rB = [x у z]T
rB = [x у z]T
The inertial velocity of dm is
v£ = (rCE + tE) = VE + rE
The momentum of dm is у dm, and of the whole airplane is
I Edm = I (V£ + rE)dm = E J dm + J tEdm
Since C is the mass center, the last integral in (4.2,5) is zero and
J xEdm = mV,, (4.2,6)
where m is the total mass of the airplane. Newton’s second law applied to dm is
dtE = Edm (4.2,7)
where d(E is the resultant of all forces acting on dm. The integral of (4.2,7) is
4 = j dfE = j *Edm
or, from (4.2,6)
f£ = mV£ (4.2,8)
The quantity /dfE is a summation of all the forces that act upon all the elements. The internal forces, that is, those exerted by one element upon another, all occur in equal and opposite pairs, by Newton’s third law, and hence contribute nothing to the summation. Thus fE is the resultant external force acting upon the airplane.
This equation relates the external force on the airplane to the motion of the CG. We need also the relation between the external moment and the rotation of the airplane. It is obtained from a consideration of the moment of momentum. The moment of momentum of dm with respect to C is by definition rfh = rX xdm. It is convenient in the following to use the matrix form of the cross product (see Appendix A. 1) so that
dhE = fExEdm
Consider
d
— (dhE) = rEEdm + rEvEdm (4.2,9)
dt
Now from (4.2,4),
rE = yE~ VE
and the moment of dt about C is
dG = г X dt
so that from (4.2,7)
dGE = rEdfE = rEEdm (4.2,10)
Equation (4.2,9) then becomes
dGl: = — (dhE) – (x, – VE)yEdm (4.2,11)
Since v X v = 0, (4.2,11) becomes
d.
dG l: — — (dhE) + ExEdm dt
Equation (4.2,12) is now integrated as was (4.2,7), and becomes
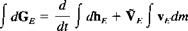 (4.2,13)
(4.2,13)
By an argument similar to that for $di, fdG is shown to be the resultant external moment about C, denoted G. fdh is called the moment of momentum, or angular momentum of the airplane and is denoted h. Formulas for h are derived in Sec. 4.3. Using (4.2,6) and noting that V X V = 0, (4.2,13) reduces to
(4.2,14)
where
The reader should note that, in (4.2,14), both G and h are referred to a moving point, the mass center. For a moving reference point other than the mass center, the equation does not in general apply. The reader should also note that (4.2,8) and
(4.2,14) are both valid when there is relative motion of parts of the airplane.
The two vector equations of motion of the airplane, equivalent to six scalar equations, are (4.2,8) and (4.2,14)
When the wind vector W is not zero, the velocity E in (4.2,5) is that of the CG relative to Fe. The angular momentum h is the same whether W is zero or not (see Exercise 4.1). Hence in the general case when wind is present the equations of motion are:
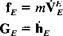 (4.2,15)
(4.2,15)
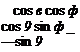 sin ф sin 9 cos ф — cos ф sin ф cos ф sin 9 cos ф + sin ф sin ф
sin ф sin 9 cos ф — cos ф sin ф cos ф sin 9 cos ф + sin ф sin ф










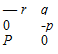



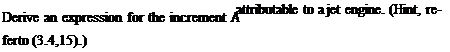
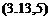 k( M)
k( M)