The first edition of this book appeared in 1959—indeed before most students reading this were bom. It was well received both by students and practicing aeronautical engineers of that era. The pace of development in aerospace engineering during the decade that followed was extremely rapid, and this was reflected in the subject of flight mechanics. The first author therefore saw the need at the time for a more advanced treatment of the subject that included the reality of the round rotating Earth and the real unsteady atmosphere, and hypersonic flight, and that reflected the explosive growth in computing power that was then taking place (and has not yet ended!). The result was the 1972 volume entitled Dynamics of Atmospheric Flight. That treatment made no concessions to the needs of undergraduate students, but attempted rather to portray the state of the art of flight mechanics as it was then. To meet the needs of students, a second edition of the 1959 book was later published in 1982. It is that volume that we have revised in the present edition, although in a number of details we have preferred the 1972 treatment, and used it instead.
We have retained the same philosophy as in the two preceding editions. That is, we have emphasized basic principles rooted in the physics of flight, essential analytical techniques, and typical stability and control realities. We continue to believe, as stated in the preface to the 1959 edition, that this is the preparation that students need to become aeronautical engineers who can face new and challenging situations with confidence.
This edition improves on its predecessors in several ways. It uses a real jet transport (the Boeing 747) for many numerical examples and includes exercises for students to work in most chapters. We learned from a survey of teachers of this subject that the latter was a sine qua non. Working out these exercises is an important part of acquiring skill in the subject. Moreover, some details in the theoretical development have been moved to the exercises, and it is good practice in analysis for the students to do these.
Students taking a course in this subject are assumed to have a good background in mathematics, mechanics, and aerodynamics, typical of a modem university course in aeronautical or aerospace engineering. Consequently, most of this basic material has been moved to appendices so as not to interrupt the flow of the text.
The content of Chapters 1 through 3 is very similar to that of the previous edition. Chapter 4, however, dealing with the equations of motion, contains two very significant changes. We have not presented the nondimensional equations of motion, but have left them in dimensional form to conform with current practice, and we have expressed the equations in the state vector form now commonly used. Chapter 5, on stability derivatives, is almost unchanged from the second edition, and Chapters 6 and 7 dealing with stability and open loop response, respectively, differ from their predecessors mainly in the use of the B747 as example and in the use of the dimensional equations. Chapter 8, on the other hand, on closed loop control, is very much expanded and almost entirely new. This is consistent with the much enhanced importance of automatic flight control systems in modern airplanes. We believe that the student who works through this chapter and does the exercises will have a good grasp of the basics of this subject.
The appendices of aerodynamic data have been retained as useful material for teachers and students. The same caveats apply as formerly. The data are not intended for design, but only to illustrate orders of magnitude and trends. They are provided to give students and teachers ready access to some data to use in problems and projects.
We acknowledge with thanks the assistance of our colleague, Dr. J. H. de Leeuw, who reviewed the manuscript of Chapter 8 and made a number of helpful suggestions.
On a personal note—as the first author is now in the 11th year of his retirement, this work would not have been undertaken had Lloyd Reid not agreed to collaborate in the task, and if Maya Etkin had not encouraged her husband to take it on and supported him in carrying it out.
In turn, the second author, having used the 1959 edition as a student (with the first author as supervisor), the 1972 text as a researcher, and the 1982 text as a teacher, wa. s both pleased and honored to work with Bernard Etkin in producing this most recent version of the book.
Toronto Bernard Etkin
December, 1994 Lloyd Duff Reid
1.1 The Subject Matter of Dynamics of Flight
This book is about the motion of vehicles that fly in the atmosphere. As such it belongs to the branch of engineering science called applied mechanics. The three italicized words above warrant further discussion. To begin with fly—the dictionary definition is not very restrictive, although it implies motion through the air, the earliest application being of course to birds. However, we also say “a stone flies” or “an arrow flies,” so the notion of sustention (lift) is not necessarily implied. Even the atmospheric medium is lost in “the flight of angels.” We propose as a logical scientific definition that flying be defined as motion through a fluid medium or empty space. Thus a satellite “flies” through space and a submarine “flies” through the water. Note that a dirigible in the air and a submarine in the water are the same from a mechanical standpoint—the weight in each instance is balanced by buoyancy. They are simply separated by three orders of magnitude in density. By vehicle is meant any flying object that is made up of an arbitrary system of deformable bodies that are somehow joined together. To illustrate with some examples: (1) A rifle bullet is the simplest kind, which can be thought of as a single ideally rigid body. (2) A jet transport is a more complicated vehicle, comprising a main elastic body (the airframe and all the parts attached to it), rotating subsystems (the jet engines), articulated subsystems (the aerodynamic controls) and fluid subsystems (fuel in tanks). (3) An astronaut attached to his orbiting spacecraft by a long flexible cable is a further complex example of this general kind of system. Note that by the above definition a vehicle does not necessarily have to carry goods or passengers, although it usually does. The logic of the definitions is simply that the underlying engineering science is common to all these examples, and the methods of formulating and solving problems concerning the motion are fundamentally the same.
As is usual with definitions, we can find examples that don’t fit very well. There are special cases of motion at an interface which we may or may not include in flying—for example, ships, hydrofoil craft and air-cushion vehicles (ACV’s). In this connection it is worth noting that developments of hydrofoils and ACV’s are frequently associated with the Aerospace industry. The main difference between these cases, and those of “true” flight, is that the latter is essentially three-dimensional, whereas the interface vehicles mentioned (as well as cars, trains, etc.) move approximately in a two-dimensional field. The underlying principles and methods are still the same however, with certain modifications in detail being needed to treat these “surface” vehicles.
Now having defined vehicles and flying, we go on to look more carefully at what we mean by motion. It is convenient to subdivide it into several parts:
|
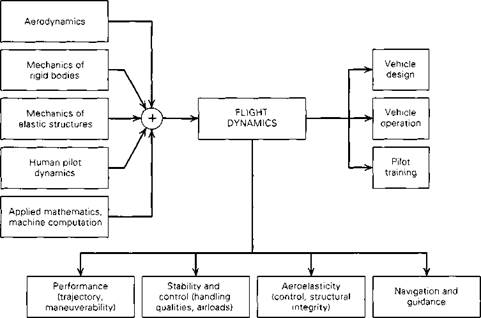
Figure 1.1 Block diagram of disciplines.
|
Gross Motion:
1. Trajectory of the vehicle mass center.1
2. “Attitude” motion, or rotations of the vehicle “as a whole.”
Fine Motion:
3. Relative motion of rotating or articulated subsystems, such as engines, gyroscopes, or aerodynamic control surfaces.
4. Distortional motion of deformable structures, such as wing bending and twisting.
5. Liquid sloshing.
This subdivision is helpful both from the standpoint of the technical problems associated with the different motions, and of the formulation of their analysis. It is surely self-evident that studies of these motions must be central to the design and operation of aircraft, spacecraft, rockets, missiles, etc. To be able to formulate and solve the relevant problems, we must draw on several basic disciplines from engineering science. The relationships are shown on Fig. 1.1. It is quite evident from this figure that the practicing flight dynamicist requires intensive training in several branches of engineering science, and a broad outlook insofar as the practical ramifications of his work are concerned.
In the classes of vehicles, in the types of motions, and in the medium of flight, this book treats a very restricted set of all possible cases. It deals only with the flight
‘It is assumed that gravity is uniform, and hence that the mass center and center of gravity (CG) are the same point.
of airplanes in the atmosphere. The general equations derived, and the methods of solution presented, are however readily modified and extended to treat many of the other situations that are embraced by the general problem.
All the fundamental science and mathematics needed to develop this subject existed in the literature by the time the Wright brothers flew. Newton, and other giants of the 18th and 19th centuries, such as Bernoulli, Euler, Lagrange, and Laplace, provided the building blocks in solid mechanics, fluid mechanics, and mathematics. The needed applications to aeronautics were made mostly after 1900 by workers in many countries, of whom special reference should be made to the Wright brothers, G. H. Bryan, L. W. Lanchester, J. C. Hunsaker, H. B. Glauert, В. M. Jones, and S. B. Gates. These pioneers introduced and extended the basis for analysis and experiment that underlies all modem practice.[1] This body of knowledge is well documented in several texts of that period, for example, Bairstow (1939). Concurrently, principally in the United States of America and Britain, a large body of aerodynamic data was accumulated, serving as a basis for practical design.
Newton’s laws of motion provide the connection between environmental forces and resulting motion for all but relativistic and quantum-dynamical processes, including all of “ordinary” and much of celestial mechanics. What then distinguishes flight dynamics from other branches of applied mechanics? Primarily it is the special nature of the force fields with which we have to be concerned, the absence of the kine – matical constraints central to machines and mechanisms, and the nature of the control systems used in flight. The external force fields may be identified as follows:
“Strong ” Fields:
1. Gravity
2. Aerodynamic
3. Buoyancy
“Weak” Fields:
4. Magnetic
5. Solar radiation
We should observe that two of these fields, aerodynamic and solar radiation, produce important heat transfer to the vehicle in addition to momentum transfer (force). Sometimes we cannot separate the thermal and mechanical problems (Etkin and Hughes, 1967). Of these fields only the strong ones are of interest for atmospheric and oceanic flight, the weak fields being important only in space. It should be remarked that even in atmospheric flight the gravity force can not always be approximated as a constant vector in an inertial frame. Rotations associated with Earth curvature, and the inverse square law, become important in certain cases of high-speed and high-altitude flight (Etkin, 1972).
The prediction, measurement and representation of aerodynamic forces are the principal distinguishing features of flight dynamics. The size of this task is illustrated
by Fig. 1.2, which shows the enormous range of variables that need to be considered in connection with wings alone. To be added, of course, are the complications of propulsion systems (propellers, jets, rockets), compound geometries (wing + body + tail), and variable geometry (wing sweep, camber).
As remarked above, Newton’s laws state the connection between force and motion. The commonest problem consists of finding the motion when the laws for the forces are given (all the numerical examples given in this book are of this kind). However, we must be aware of certain important variations:
1. Inverse problems of first kind—the system and the motion are given and the forces have to be calculated.
2. Inverse problems of the second kind—the forces and the motion are given and the system parameters have to be found.
3. Mixed problems—the unknowns are a mixture of variables from the force, system, and motion.
Examples of these inverse and mixed problems often turn up in research, when one is trying to deduce aerodynamic forces from the observed motion of a vehicle in flight or of a model in a wind tunnel. Another example is the deduction of harmonics of the Earth’s gravity field from observed perturbations of satellite orbits. These problems are closely related to the “plant identification” or “parameter identification” problem of system theory. [Inverse problems were treated in Chap. 11 of Etkin (1959)].
TYPES OF PROBLEMS
The main types of flight dynamics problem that occur in engineering practice are:
1. Calculation of “performance” quantities, such as speed, height, range, and fuel consumption.
2. Calculation of trajectories, such as launch, reentry, orbital and landing.
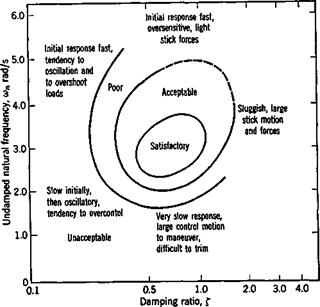
3. Stability of motion.
4. Response of vehicle to control actuation and to propulsive changes.
5. Response to atmospheric turbulence, and how to control it.
6. Aeroelastic oscillations (flutter).
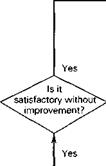
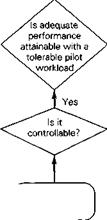
7. Assessment of human-pilot/machine combination (handling qualities).
It takes little imagination to appreciate that, in view of the many vehicle types that have to be dealt with, a number of subspecialties exist within the ranks of flight dynamicists, related to some extent to the above problem categories. In the context of the modern aerospace industry these problems are seldom simple or routine. On the contrary they present great challenges in analysis, computation, and experiment.
![Axes and Notation Подпись: Figure 1.6 Notation for body axes. L = rolling moment, M = pitching moment, N = yawing moment, p = rate of roll, q = rate of pitch, r = rate of yaw. [X, K, Z| = components of resultant aerodynamic force. u. v, w] = components of velocity of C relative to atmosphere.](/img/3129/image010_4.gif)
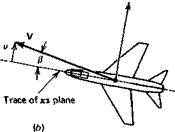
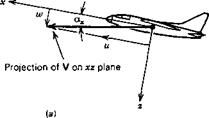
 Angle of attack, ax = tan’
Angle of attack, ax = tan’