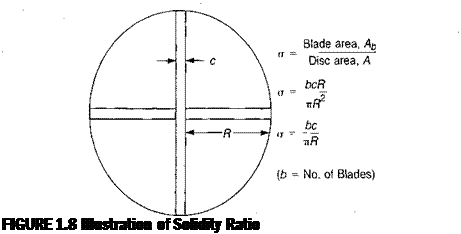
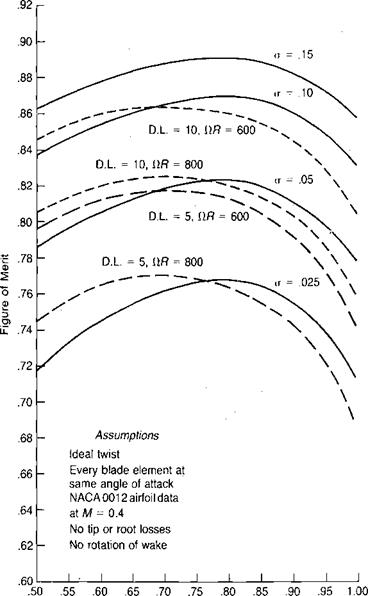
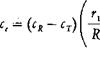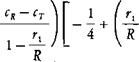Tip Loss and Root Loss
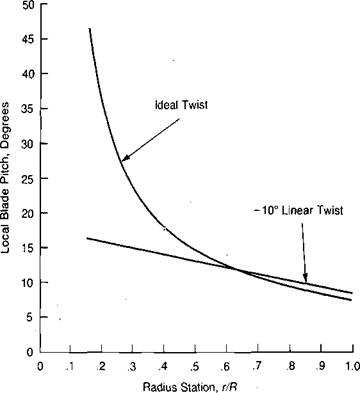
The lift of a rotor blade—or of a wing—goes to zero at the extreme tip, but it starts falling off some distance inboard. Thus the integration of the equation for rotor lift to the extreme tip is somewhat optimistic. A similar optimism, though of somewhat lesser importance, is introduced by’ starting the integration at the center of the rotor even though the blade "cutout” may be 10% to 25% of the radius. Figure 1.16 shows the theoretical and realistic lift distributions for a blade with
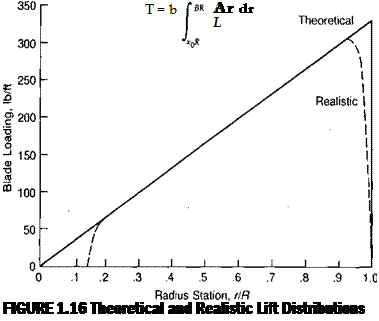 |
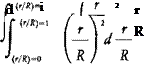
ideal twist. A numerical method for computing the shape of the lift distribution at the tip has been developed for propeller analysis and adapted for rotors in Reference 1.3. This method, known as the Goldstein-Lock method, is sometimes incorporated in digital computer hover performance programs. A more convenient scheme, however, is to use modified limits of integration such that:
where x0 is the fraction of root cutout and BR is the effective outer radius, which is picked such that the area under the theoretical lift distribution out to BR is the same as the area under the actual curve out to JR. The amount of the tip loss is dependent on the total lift of the blade and its geometry. The higher the lift, and the wider the chord with respect to the radius, the further inboard the lift starts falling off. Both these effects are included in an empirical equation for В that was first derived by Prandtl and gives satisfactory correlation with the Goldstein-Lock calculations for lightly loaded rotors.
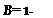 [гс~т
[гс~т
b
For the main rotor of the example helicopter hovering at sea level, the equation gives an effective radius factor, B, of 0.97.
|
T A(B[1]-xl) |
When root and tip losses are accounted for, the momentum equations previously derived should be modified. This can be done by defining an effective disc loading, D. L.cff, based on the effective disc area, which is smaller than the true area:
Thus:
For the example helicopter,
D. L. = 7.1 lb/ft2
|
•972 — .15 |
|
= 7.7 lb/ft2 |
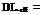
But
Thus at sea level
vle((= l4.5y/lJ = 40.2 ft/sec
instead of the 39 ft/sec previously calculated.
With root and tip losses accounted for, the equation for Ct/g becomes:
CT/o=(B2 —*^(Є, — ф,)
The value of the induced angle, ф„ now must be based on only the effective disc area, although the definitions of the nondimensional coefficients are still based on the geometric rotor radius. Thus ф, becomes:
![]()
![]()
![]()
CT
2 (B2-xl)
gCj/g
|
4 Ct/g I gCt/g a (.В2 – Xq) 2 (B2 — Xq) |
Solving the equation for Ct/g gives for pitch at the blade tip, 0;:
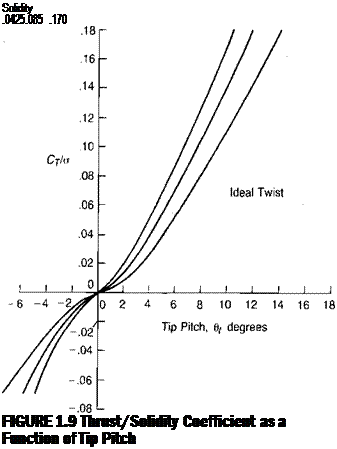
For the example helicopter with an ideally twisted rotor, the tip pitch required at the design hover condition is 7.1° instead of the 6.7° calculated. without the losses. Since the lift falls off toward the tip, the induced drag also falls off, but the profile drag does not. At the root, there may not be any lifting surface, but there is always a spar or a section of the hub that has drag even if it has no lift. Thus the profile drag must be integrated from root to tip. Considering the increased inflow angle due to the decrease in effective disc area, the expression for Cp/a of a rotor with ideal twist is:
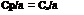 aCr/a cd 2 (B2-xi) +~8
aCr/a cd 2 (B2-xi) +~8
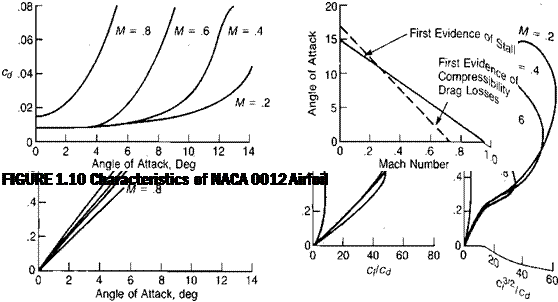
The drag coefficient for use in this equation should be found from airfoil data such as in Figure 1.10 and an average angle of attack, which is:
![]() _ 57.3Ct/g
_ 57.3Ct/g
CL =- ;—- V
B2-x20
For the example helicopter with ideal twist, this method gives the rotor power required for hover at the design gross weight as 1,840 horsepower if root and tip losses are not considered and 1,900 horsepower if they are, a difference of about 3.2%.
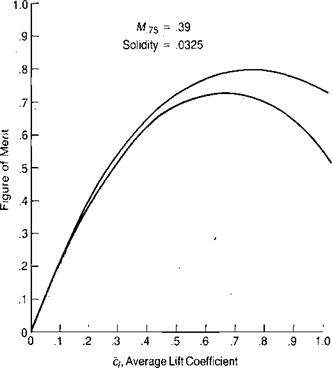
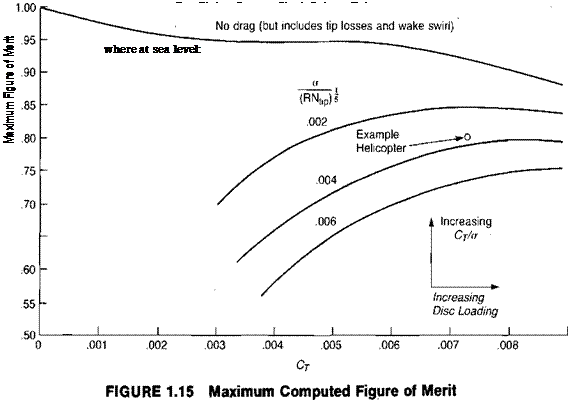
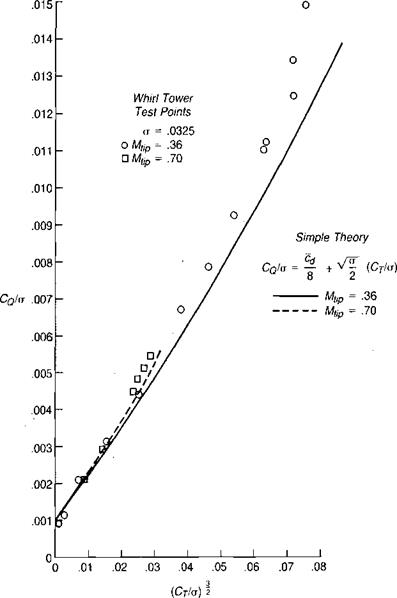
There is no easy way to verify experimentally the simple hover tip loss equation, but it may at least be partially justified by comparing the results of hover calculations made using it with those made using the more sophisticated prescribed wake vortex method. Figure 1.17 shows the calculated ideal Figure of Merit, assuming no profile drag, as it is affected by number of blades. The solid line is from reference 1.2 and was calculated for uniform inflow using a prescribed wake vortex method. The dashed line is for a rotor with ideal twist and is based on the reduction of disc area due to root and tip losses and also includes the effect of wake rotation, as discussed in a later section. It may be seen that the shape of the two lines is essentially the same, indicating that the simple tip loss equation is in good company.











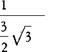
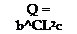 R2a I (0, – ф,)фtrdr + cd I r’dr
R2a I (0, – ф,)фtrdr + cd I r’dr