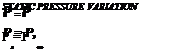The vortex-ring state
For low rates of descent, that is when the vertical velocity is less than the induced velocity (f < 0.5), the rotor is said to be operating in the vortex-ring state. As the rotor descends with power in this state, it is effectively pumping air from beneath the rotor by the action of the vortex ring located in-plane with the rotor. At high power settings, it is possible to pump so much air from beneath the rotor that the rate of descent increases thereby exacerbating the problem. The pilot may attempt to arrest the rate of descent by application of increased collective pitch but this tends to increase the rate of descent still further. If on the other hand the pilot lowers the collective lever the thrust is reduced and the helicopter also increases its rate of descent. This dangerous phenomenon is often called power settling. It can cause helicopters to develop significant rates of descent when operating below maximum gross weight even when full torque is applied.
Care must be taken to avoid entry into vortex ring particularly when hovering without external references at high altitude and when making steep approaches. Operation of the rotor in a state of fully developed vortex ring can be prevented by avoiding vertical descents at rates between 70% and 150% of vih (1700 to 3600 ft/min for the example helicopter). However vertical descents at modest speeds may be required operationally in these circumstances: the onset of significant vibration; a sudden uncommanded increase in the rate of descent; or a tendency for the helicopter to gyrate in pitch and roll, are taken as indicators of the incipient stages of power settling or the vortex ring condition and recovery action is initiated.
Other causes of vortex ring are the application of a high collective setting in a flare manoeuvre or operating in an upflow (equal to vi) close to a cliff. It should be noted that yaw manoeuvres can establish a vortex-ring state in the tail rotor.











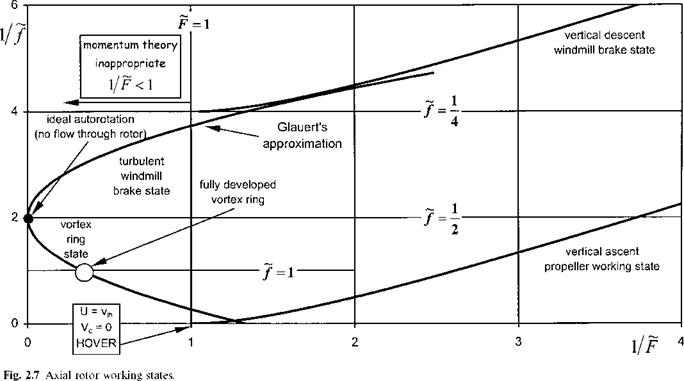
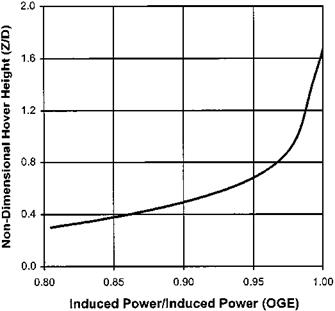
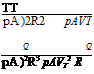 CT =
CT =