Induced drag
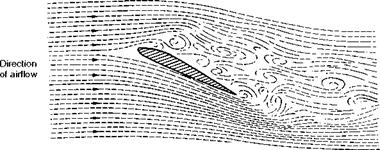
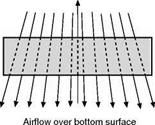
Experiments with smoke or streamers show quite clearly that the air flowing over the top surface of a wing tends to flow inwards (Fig. 3.27, overleaf). This is because the decreased pressure over the top surface is less than the pressure outside the wing tip. Below the under-surface, on the other hand, the air flows outwards, because the pressure below the wing is greater than that outside the
|
|
|
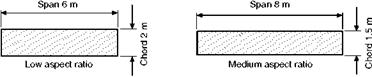
Fig. 3.26 Aspect ratio The area of each wing is 12 m2. |
wing tip. Thus there is a continual spilling of the air round the wing tip, from the bottom surface to the top. Perhaps the simplest way of explaining why a high aspect ratio is better than a low one is to say that the higher the aspect ratio the less is the proportion of air which is thus spilt and so is ineffective in providing lift – the less there is of what is sometimes called ‘tip effect’ or ‘end effect’.
When the two airflows, from the top and bottom surfaces, meet at the trailing edge they are flowing at an angle to each other and cause vortices rotating clockwise (viewed from the rear) from the left wing, and anti-clockwise from the right wing. All the vortices on one side tend to join up and form one large vortex which is shed from each wing tip (Fig. 3.28). These are called wing-tip vortices.
All this is happening every time and all the time an aeroplane is flying, yet some pilots do not even know the existence of such vortices. Perhaps it is just as well, perhaps it is a case of ignorance being bliss. In earlier editions of this book it was suggested that if only pilots could see the vortices, how they would talk about them! Well, by now most pilots have seen the vortices or, to be more correct, the central core of the vortex, which is made visible by the condensation of moisture caused by the decrease of pressure in the vortex (Figs ЗА and 3B, overleaf). These visible (and sometimes audible!) trails from the wing tips should not be confused with the vapour trails caused by condensation taking place in the exhaust gases of engines at high altitudes (Fig. 3C, overleaf).
 |
 |
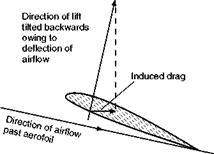
Now if you consider which way these vortices are rotating you will realise that there is an upward flow of air outside the span of the wing and a down-
ward flow of air behind the trailing edge of the wing itself. This means that the net direction of flow past a wing is pulled downwards. Therefore the lift – which is at right angles to the airflow – is slightly backwards, and thus contributes to the drag (Fig. 3.29). This part of the drag is called induced drag.
In a sense, induced drag is caused by the lift; so long as we have lift we must have induced drag, and we can never eliminate it altogether however cleverly the wings are designed. But the greater the aspect ratio, the less violent are the wing-tip vortices, and the less the induced drag. If we could imagine a wing of infinite aspect ratio, the air would flow over it without any inward or outward deflection, there would be no wing-tip vortices, no induced drag. Clearly such a thing is impossible in practical flight, but it is interesting to note that an aerofoil in a wind tunnel may approximate to this state of affairs if it extends to the wind-tunnel walls at each side, or outside the jet stream in an open jet type of tunnel. The best we can do in practical design is to make the aspect ratio as large as is practicable. Unfortunately a limit is soon reached – from the structural point of view. The greater the span, the greater must be the wing strength, the heavier must be the structure, and so eventually the greater weight of structure more than counterbalances the advantages gained. Again it is a question of compromise. In practice, aspect ratios for flight at subsonic speeds vary from 6 to 1 up to about 10 to 1 for ordinary aeroplanes, but considerably higher values may be found on sailplanes, and even more in man-powered aircraft, where aerodynamic efficiency must take precedence over all other considerations (see Fig. 3D, later) and very low values for flight
|
|
Fig ЗА Wing-tip vortices
(By courtesy of the former British Aircraft Corporation, Preston)
The low pressure at the core of the vortex causes a local condensation fog on a damp day.

Fig 3B Rolling up of vortices
(By courtesy of the former British Aircraft Corporation, Preston)
A unique demonstration of the rolling up process; the wing tip and flap tip are each shedding vortices that are strong enough to cause condensation, and the pair roll around one another.
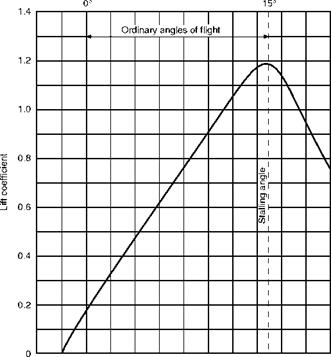
at transonic and supersonic speeds (see Fig. 3E, later). Fig. 3.30 shows how aspect ratio affects the lift curve, not only in the maximum value of CL but in the slope of the curve, the stalling angle actually being higher with low values of aspect ratio. Notice that the angle of no lift is unaffected by aspect ratio.
The theory of induced drag can be worked out mathematically and experiment confirms the theoretical results. The full calculation involved would be
 Direction of airflow at a distance from aerofoil
Direction of airflow at a distance from aerofoil
|
Fig3C Exhaust trails (By courtesy of General Dynamics Corporation, USA) A modified B36 with 6 piston engines and 4 jet engines, and carrying an atomic reactor as an experiment on the shielding of crews and aircraft components. |
|
|
out of place in a book of this kind, but the answer is quite simple and the reader may like to know it, especially since it helps to give a clearer impression of the significance of this part of the drag.
The coefficient of induced drag is found to be Cl2//tA for wings with an elliptical planform, where A is the aspect ratio and CL the lift coefficient (the value for tapered wings may be 10 per cent to 20 per cent higher, depending on the degree of taper). This means that the actual drag caused by the vortices is (Cl2//tA) .jpV2 . S, but since the TpV2 . S applies to all aerodynamic forces, it is sufficient to consider the significance of the coefficient, Cl2//tA . In the first place, the fact that A is underneath in the fraction confirms our previous statement that the greater the aspect ratio, the less the induced drag; but it tells us even more than this, for it shows that it is a matter of simple proportion: if the aspect ratio is doubled, the induced drag is halved. The significance of the CL2 is perhaps not quite so easy to understand. CL is large when the angle of attack is large, that is to say when the speed of the aircraft is low; so induced drag is relatively unimportant at high speed (probably less than 10 per cent of the total drag), more important when climbing (when it becomes 20 per cent or more of the total) and of great importance for taking off (when it may be as high as 70 per cent of the total). In fact, the induced drag is inversely proportional to the square of the speed, whereas all the remainder of the drag is directly proportional to the square of the speed.
It is easy to work out simple examples on induced drag, e. g. – A monoplane wing of area 36 m2 has a span of 15 m and chord of 2.4 m. What is the induced drag coefficient when the lift coefficient is 1.2?
Aspect ratio = A = 15/2.4 = 6.25
Induced drag coefficient = Cl2//tA 5 1.22/6.25/r = 0.073
Perhaps this does not convey much to us, so let us work out the actual drag involved, assuming that the speed corresponding to a CL of 1.2 is 52 knots, i. e. 96 km/h (26.5 m/s), and that the air density is 1.225 kg/m3.
Induced drag = (Cl2//tA ) . іpV2 . S
= 0.073 X і X 1.225 X 26.52 X 36 2
= 1130 N
Fig 3D High aspect ratio (opposite)
(By courtesy of Paul MacCready)
The Gossamer Condor. Flight on one man-power requires a very high value of lift/drag.
|
|
Let us take it even one step further and find the power required to overcome this induced drag –
Power = DV = 1130 3 26.5 = 30 kW (about 40 horse-power).
This example will help the reader to realise that induced drag is something to be reckoned with; it is advisable to work out similar examples, which will be found at the end of the book.