Most aerospace vehicles consist of more than one body. Aircraft have, besides their basic airframe, rotating machinery like propellers, compressors, and turbines; and, as moving parts, control surfaces and landing gears. Missiles possess control surfaces and sometimes even spinning parts for stabilization. Certainly, you have heard of the Hubble telescope and its control momentum gyros, which point the aperture within a few microradians.
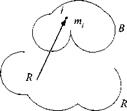
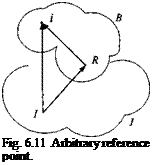
To calculate the total angular momentum, we could simply sum over all of the particles of all of the bodies in the cluster. This approach would bring no new insight. Instead, we derive a formula that takes the individual known angular momenta and combines them to form the total angular momentum (see Fig. 6.9).
Theorem: The angular momentum of a collection of rigid bodies B^, к =
1, 2, 3,… (with their respective centers of mass В*) relative to a reference frame R and referred to one of its points R is given by
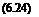 4”‘‘ = £ {П>ак+»"‘s«,0
4”‘‘ = £ {П>ак+»"‘s«,0
к
|
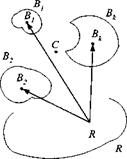
Fig. 6.9 Cluster of rigid bodies.
|
The individual points В* can be moving relative to each other, but the bodies themselves must be rigid.
Proof: The proof follows from the additive properties of angular momenta [Eq. (6.17)], and the separation into rotary and particle terms [Eq. (6.18)]. To get the total angular momentum, we sum over all individual bodies
_ ‘ jBkR
lR ~ / ,lR
к
and adopt Eq. (6.18) for each body В*
lBRtR =IBBl^R+mB^SBlRvl
to prove the theorem
к
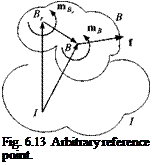
Equation (6.24) makes a general statement about clustered bodies. For many applications, like aircraft propellers, turbines, helicopter rotors, dual-spin satellites and flywheel stabilizers, this relationship can be simplified. In these cases the c. m. of the individual bodies are mutually fixed and so is the common c. m. Introducing this common c. m. C as reference point leads to a simpler formulation.
Theorem: If the common c. m. C of the cluster of bodies T. B*. is introduced
as reference point and if the individual c. m. B>: do not translate wrt C, then the angular momentum of the entire cluster wrt to the reference frame R and referred to the common c. m. C is
lcBtR = + (Y, rnB>SBkCSBtc^ u, CR (6.25)
Compare Eqs. (6.25) and (6.24). The linear velocity vRt does not appear any longer because we adopted the common c. m. (just as in the single-body case). Following earlier convention, we distinguish the two terms as rotary and transfer
contributions. The second term concentrates the mass of body frame Bk in its c. m. Ви for the angular momentum calculation. According to Eq. (6.8), derived from the Huygen’s theorem, the term in parentheses is the MOI of all of the individual body masses mBk referred to the common c. m. The vector uiCR relates the angular velocity of frame C, consisting of the points Bk, to the reference frame R.
Proof: To prove this theorem, some stamina is required. The easier path is to accept the theorem and drop down to the example. For the proof we take three steps:
1) Introduce the vector triangle to include the total c. m. C
sBkR = SBkC +SCR
into Eq. (6.24)
{RBtR — ^2ііВвкшВкЕ + £«B‘(^c + SCr)Dr(sBiC +sCr)
and execute the multiplications
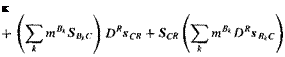 (6.26)
(6.26)
The last two terms are zero because C is the common c. m. Let us demonstrate this fact for the last term. Because the body’s mass is a constant scalar, it can be brought inside the rotational derivative, and the summation can be exchanged with the time derivative, resulting in
2) Now let the arbitrary reference point R be the common c. m., then Sen — Scc = 0, and the second term of Eq. (6.26) is zero. We are left with two terms:
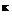
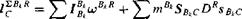 (6.27)
(6.27)
The first term is the sum of all rotary angular momenta. The second term is expanded by transforming the rotational derivative to the frame C:
£mBkSBkcDRsBkc = £«tB‘SBtc(£>cSBtc + ftCRSBkc)
— ^^mBk^BkcDcSBkc + m Вк S Bk(‘^lCRs вк с
3)
In addition, because the individual c. m. Bk and the common c. m. C are fixed in frame C, DcsBkC = 0, and the first term is also zero, leaving Eq. (6.27) with
The last term can be modified by a procedure we have used before [see Eq. (6.21)], and thus the proof is complete:
lcBtR = T, lfaBk* +
Quite frequently, in aerospace applications one of the bodies is the main body, supporting all other spinning bodies. It takes on the function of frame C, but its own c. m. is not the common c. m. C. If that body is called Вi, then the theorem becomes
Example 6.6 Propeller Airplane
Problem. Determine the angular momentum of a single propeller-driven airplane wrt the inertial frame I. The propeller P with mass mp and c. m. P is displaced from the reference point T at the tip of the airplane by SpT. The c. m. В of the airframe В with mass mB is displaced from T by Sbt- Their MOI are Ip and Ip and their angular velocities uipn and шш, respectively.
The components of the tensors in airframe coordinates are for the propeller
|
Co
II
|
1
0 О
<N
° ^
►5 °
1 ___
|
, [vPB]B =
|
3 °
1____
|
, [■У/>г]В =
|
Spn
0
|
|
1
О
О
*■4
|
|
0
|
|
0
|
and for the airframe
|
Iflii
0
|
0
ІВ2
|
1
CO
CQ О
|
, WBI}B =
|
1
_______ 1
|
. [^вг]в =
|
SBTl
0
|
|
Івп
|
0
|
ffl33
|
|
r
|
|
0
|
Solution. To determine the total angular momentum, we apply Eq. (6.25), referred to the inertial frame /:
tcBkI = Т, ІВвУкІ + (Y, mBkSBkCSB^ 0JCI
We are dealing with the propeller P and the airframe В serving as frame C:
lcBiI = Ір(шрв + шш) + Іввшві + mp S pc SpCu! BI + mB SBCSBCu>BI (6.28)
To determine the individual c. m. displacement vectors sPc and sBc, we first get the location of the common c. m. C from the reference point T
 mBsBT + mpSpT
mBsBT + mpSpT
im8 + mp)
and then the desired c. m. locations wrt the common c. m.
Spc = Spr — Sct $BC = Sflr — Scr
By eliminating scr.
We have derived the solution in an invariant form, represented by Eqs. (6.28) and
(6.29) .
For developing the component form, we express Eq. (6.28) in airframe coordinates ]B
(6.30)
|
and then insert the components. Multiplying the matrices yields
|
№BtI]B –
|
Ip(p + шр) + ІвіР + Івізг
(ІР2 + iBi)q
|
+ {mP4a +mBs2Bcl)
|
"О"
ч
|
|
(ІРЗ + ІВ2з)г + ІВзР
|
|
r
|
|
(6.31)
where spci and ідеї are the first components of the vectors in Eq. (6.29). The second term affects only the pitch and yaw angular momenta.
Frequently, several simplifications are justified. With mp p and mpSpC1 » mBs2Ba we can reduce Eq. (6.31) to
|
№вк1}в =
|
Ipo>P + ІвпР + Івізг (Ір2 + lBi)q
|
+ m? sPC
|
‘О
q
|
|
(Ірз + ІвззУ + 1взР
|
|
г
|
More drastically, the second term and the product of inertia Ів в are sometimes dropped (only the principal MOIs IBi, IB2, and /B3 are left), and the MOI of the propeller is assumed much smaller than that of the airframe. Then we arrive at a popular representation that just adds the angular momentum of the propeller to that of the airframe:
![Angular Momentum of Clusters of Bodies Подпись: [/cBkI]B](/img/3132/image434_1.gif) 1рШр + IBp ІВ2Ч ІВЗГ
1рШр + IBp ІВ2Ч ІВЗГ
Another entity, the angular momentum, has joined our collection of building blocks, but it is more sophisticated than the other items. It requires three defining super – and subscripts. The first frame represents the material body, followed by an arbitrary reference frame and a reference point. Frequently, the reference point is the c. m., and an inertial frame serves as reference. This situation arises in particular when we formulate the attitude equations of flight vehicles from Euler’s law.
![]() h oo 0 /2 0 0 0 h
h oo 0 /2 0 0 0 h![]() ~dco‘
~dco‘












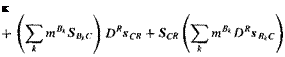 (6.26)
(6.26)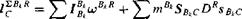 (6.27)
(6.27)
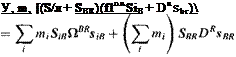
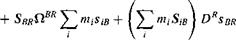 (6.20)
(6.20)