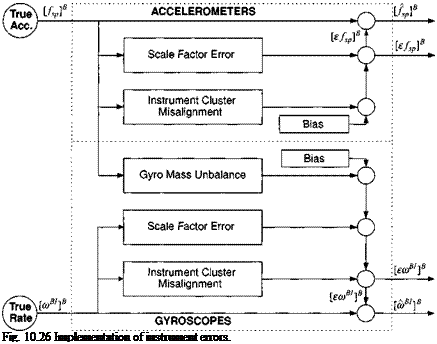
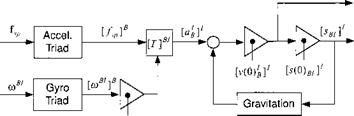
Advanced guidance law
Proportional navigation, born in the waning days of World War II, is revalidated by modern control. We will employ optimal control techniques to derive the advanced guidance law in Cartesian coordinates. It can be shown that it encompasses the classical PN law, expressed in polar coordinates. The guidance command is a function of relative position and velocity and the time-to-go until intercept rg0. Of particular importance for the performance of this advanced guidance law (AGL) is the accurate calculation of fg0. It depends on the missile and the (unknown) target motions. I will derive the so-called circle time-to-go, based on circular engagements, which performs quite well in close-in engagements.
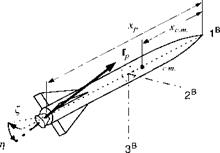
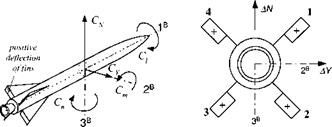
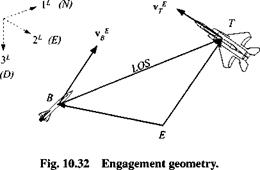
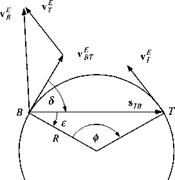
Before we can formulate the optimality problem, we investigate the engagement geometry. Figure 10.32 shows the missile В flying an intercept against target aircraft T. For this derivation we use the Earth E as the inertial reference frame, as it is common practice for air-to-air missiles, and the local-level coordinate system
]L. The displacement of the target wrt the missile is the difference between their displacements relative to the Earth reference point E
sTb = ste — sbe
Taking the rotational derivative wrt the inertial reference frame E
E>estb = DesTe — Desbe
produces the differential velocity v EB from the two relative velocities of Fig. 10.32
vEB=vE-vE
Refer back to Example 4.6 to renew your understanding of differential and relative velocities. A second derivative yields the differential accelerations aEB
Deveb = Deve — DEvB
E EE
aTB = aT ~ aB
composed of the relative accelerations. If we pick the ]L coordinate system, the rotational derivative becomes the ordinary time derivative, and we have
![]() = НІ~НІ (Ю.104)
= НІ~НІ (Ю.104)
Now we apply Newton’s law to the missile, with /sp the specific force and g the Earth’s gravitational attraction, and express it in ]L coordinates
Hf = i/spi" + [g]"
Substituting into Eq. (10.104) yields
![]()
 |
= H f – ([/sp]" + [g]") (10.105)
We neglect the target and gravity accelerations and interpret the specific forces as an instantaneous response to the acceleration command и = —[/sp]1". Furthermore,
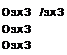 |
||||
we introduce some simplifications in nomenclature: As = [sjb]1; Av = vfBL x — [As Av]. Then the state-space formulation is
Note the very simple form of the dynamic equations. It is amazing how useful they are in applications.
We have made all preparations for the formulation of the optimal guidance problem. For you to follow the derivation, you should be familiar with the foundations of optimal control or consult Stengel22 when you get lost.
Example 10.1 Optimality Problem
Problem. Find the control u(x. t) that minimizes the cost function
![]() 1 1 Ґ
1 1 Ґ
J = – x(tf)Sx(tf) + – J
![]() subject to the dynamic constraint x = Fx –
subject to the dynamic constraint x = Fx –
The performance index combines two important criteria for a successful inter’ cept. It minimizes the miss distance and limits the control power. The first term includes the weighting matrix S, which selects the square of terminal miss As(fy) from the state vector and weighs equally every component by ss.
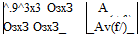 ^x(tj)Sx(tj) — [As(tf) Av(f/)]
^x(tj)Sx(tj) — [As(tf) Av(f/)]
= ^■As(tf)As(tf)
The square of the controls are integrated over the engagement time, weighted by the 3 x 3 matrix R = r/3×3 and minimized. Apportioning values for ss and r emphasizes either the reduction in terminal miss or in control.
Solution. Introduce the Hamiltonian
H = jURu + A (Fx + Gu)
The optimal solution for u(x, t) consists of the adjoint equation in the costate A
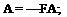 X(tf) = Sx(tf)
X(tf) = Sx(tf)
and the optimality condition
![]()
![]() ґдН
ґдН
which provides the optimal guidance solution
u = – R’GX (10.108)
we just have to eliminate A.
For the elimination of X, you need to substitute Eq. (10.108) into Eq. (10.106) and combine it with Eq. (10.107) to get the state equations augmented by the costate
These linear differential equations can be solved using the state transition matrix Ф(г, to), which can be expressed in the fundamental matrix A of Eq. (10.109):
ф(г, r0) = eA(t~tB) = 112×12 + (t – to)A + (t~l°)2A2 + (t~f°)3A3 The state transition matrix is partitioned for x and A (assuming to = 0):
 x(tj
x(tj
X(t)
(10.110)
Notice that Ф21 is zero. The state transition matrix can also be used to solve the differential equations from any time t to final intercept time tf. This gives us the opportunity to introduce the time-to-go parameter fg0 = tf — t
Ф(?f, t) = Ф(tf-t) = Ф(Г80) Applied to Eq. (10.110), we obtain
![]() Фіі(^>о) Фі2(%о) x(t)
Фіі(^>о) Фі2(%о) x(t)
Обхб Ф22(%о)_ _A(t)_
From the first equation, after premultiplying by S, we get one expression
Sxf – 5Фц((6о)і + S<t>n(tzo)X
From the second equation we derive А/ = Фг2(^о)А, which is equal to Sxf according to Eq. (10.107):
Sx f — Ф22(^о)^“
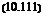 Combining both, we can eliminate x/ and solve for A in terms of x A = [Ф22(??о) – £Фі2(Г§о)]-1£Фп(Г8о)л:
Combining both, we can eliminate x/ and solve for A in terms of x A = [Ф22(??о) – £Фі2(Г§о)]-1£Фп(Г8о)л:
Now we can replace A in Eq. (10.108) and obtain the optimal solution solely as a function of the state де.
The optimal solution of guidance law consists of a gain multiplied by the state
u = K(tg0)x (10.112)
where
K(tgo) = – R~’GT[<S>22(tgo) – 5Фі2(%о)]_15Фп(%о) (10.113)
The guidance gain K(tg0) can be computed onboard the missile. It is a function of time-to-go, introduced through the state transition matrices. The other matrices are constant. To implement the guidance law, the differential position and velocity x — [As Av 1; As = sTb]l’, Av = [VjgL must be available to the missile guidance processor. This is by no means easily accomplished. IR seekers provide only LOS rates, which are insufficient for reconstructing the full state. RF seekers, on the other hand, measure range and range rate. They possess sufficient intelligence for the full state, but require a rather sophisticated Kalman filter. Possibly, the ultimate solution is the so-called third-party targeting. A surveillance platform downlinks accurate target position and velocity information to the missile. Onboard the missile the differential position and velocity are then formed in support of the guidance law.
The gain includes a matrix inversion, which can be executed algebraically. First we substitute the values from Eq. (10.110)
![]()
Substituting into Eq. (10.112) and replacing the state by the differential position and velocity results in the control equation
(10.114)
![]() If the control vector is not weighted, i. e., if unlimited control power is available, then r = 0, and Eq. (10.114) simplifies to the form of the actual AGL
If the control vector is not weighted, i. e., if unlimited control power is available, then r = 0, and Eq. (10.114) simplifies to the form of the actual AGL
![]() (10.115)
(10.115)
with N = 3.
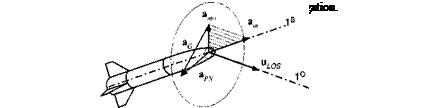
AGL is the PN law in Cartesian coordinates. It identifies the optimal PN gain as three. However, several air-to-air missiles operate with a higher gain—around four—to tighten up the guidance loop and to reduce the miss distance. Sometimes, the gain may even be scheduled as a function of the closing speed. In all cases, the selection must be based on extensive engagement studies that require full six-DoF fidelity and realistic noise models.
The implementation of AGL in a simulation takes the differential position and velocity from computed target and INS data [ігв]1"* [VjB]l and sends the acceleration command in body axes to the autopilot.
![]()
(10.116)
What remains to be discussed is the calculation of time-to-go.
The quality of the guidance depends on the accuracy of the time-to-go estimate. If the future trajectory were precisely known, fg0 could be calculated error free. However, because the target is uncooperative, the missile trajectory cannot be predicted with certainty. Therefore, certain assumptions are made about both the missile and the target. The most obvious one being the straight-line extrapolation from the current conditions. Yet close-in combat is fought in circles, and these are the stressing conditions that the guidance law must excel under. We shall therefore base our fg0 estimate on circular engagements.
Figure 10.33 shows the geometry of a particular circular engagement. We assume that the differential velocity vfr of the missile В wrt the target T is tangential to a circle that contains both points with their displacement vector s tb ■ If the differential missile velocity remains on the circle and is constant, we can calculate the time until intercept from it and the length of the arc <pR:
(pR
You can calculate the arc length by first determining the angle 8 from the scalar product of the two vectors [vBTL and [ігв]1-:
then expressing
є = 90 deg — 8
|
Fig. 10.33 Circle engagement. |
and
ф = 180 deg — 2s — 28
with
D krai
" — T———
2 cose
yields the arc length. The onboard guidance processor continually updates the time to go based on the v ‘Hr and Sjb intelligence. If the missile does not follow a circle, but executes a head-on straight-line engagement, ф = 0 and R — оо, and the calculation breaks down. This happens rarely in air-to-air engagements. If it occurs, it lasts only for a few integration steps, and you can program around it. I have had very good results for close engagements, and no problems with long fly-out trajectories.
10.2.5.3 Summary. As a faithful follower of my exposition, you should have a good grasp of the most important guidance laws for missiles: proportional navigation, compensated proportional navigation, and the advanced guidance law. Yet be forewarned; many variants of these basic schemes will pop up in missile simulations. I hope that you will recognize them as such and become emboldened to build your own.
10.2.4 IR Seeker
In Sec. 9.2.5 you read about the basic principles of IR sensors. You may have applied them to the gimbaled model that was introduced there. If you have working code, you can drop it straight into your six-DoF simulation and start flying.
In this section we will develop another IR seeker, based on the current state of the art. Its mechanical arrangement consists of an outer roll and inner pitch gimbal. The focal plane array incorporates 128 x 128 elements with a resolution of 0.5 mrad and a total field of view of 3.6 deg. In clear atmosphere the detection range is 12 km. A particularly interesting feature is the so-called virtual gimbals,
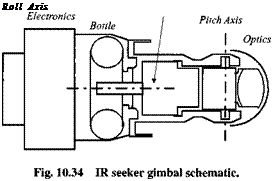 |
which mechanize standard yaw and pitch gimbals in software. We deal therefore with two transformations, the physical gimbals of roll and pitch and the computer gimbals of yaw and pitch.
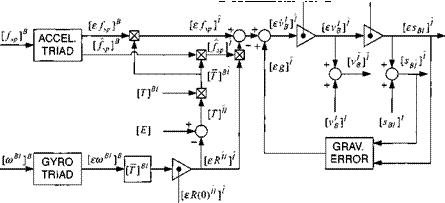
Unfortunately, the modeling task gets more complicated. Seeker kinematics is described by several transformations, and the focal plane geometry requires careful considerations. Adding uncertainties and errors poses further challenges.











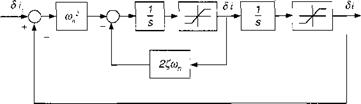
![Compensated proportional navigation Подпись: = [apN]°](/img/3132/image1039.gif)

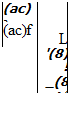 (flPK)f sec if OB + dm tan jf0B
(flPK)f sec if OB + dm tan jf0B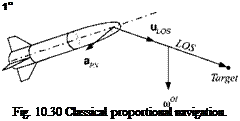
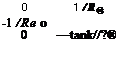
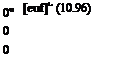
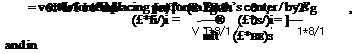
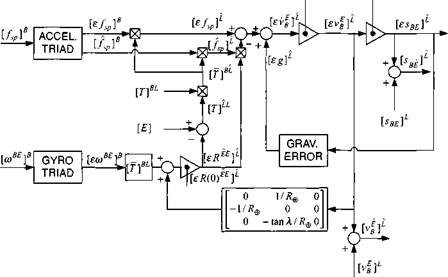

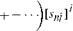
![. Error equations for space-stabilized navigators Подпись: Table 10.1 Perturbations of INS variables Variable Perturbation Velocity HI' - к I'-M' Position [«Bll' — [%■] ' - [SBI]' Specific force [eU]B = [/sp] Iй - l/sp]fi Gravitational acceleration teg]' = = [g]' - [g]' Coordinate transformation m" = [E]' - ■ [eR'1]'](/img/3132/image1010.gif)