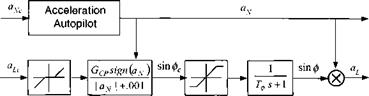
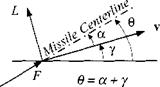
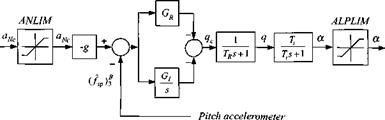
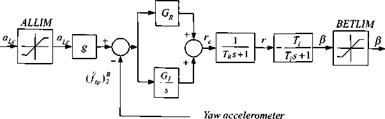
Line guidance, vector case
If you are theoretically inclined and want to see some vector and tensor mechanics in action, you will like this general derivation of line guidance. We will start with the two conditions for line guidance, derive the vector form, convert it to tensors, and eventually express it in matrices for programming. Equations (9.59) and (9.61) will be fully recovered.
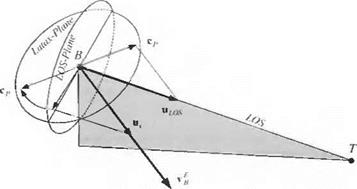
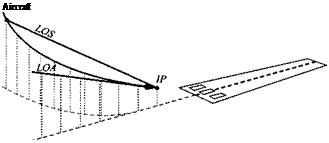
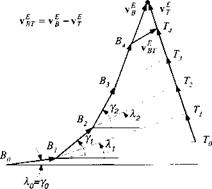
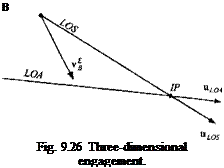
The principle of line guidance is stated as follows (see Fig. 9.26): If the vehicle В is positioned on the LOA and the velocity vector v § points at the target, then the two vector products of the unit vectors mLOs and Hloa are zero:
єР = F|hLos = 0 and eL = У|иШа = 0 (9.62)
Єр is the so-called point attack error, employed to correct LOS errors, and eL is the line attack error, used to bias the velocity vector towards the LOA. If both errors are zero, the vehicle flies on the LOA toward the target. We combine them with the variable gain G for the total error vector
є = Єр — G Єр (9.63)
Єї opposes Єр until the vehicle has reached the LOA. For this reason the Сєь term is also called the line bias term.
The commanded acceleration is the vector product of the total error є and the velocity vector Vuv multiplied by a constant gain К (note A is the skew-symmetric form of є):
a — KVEuv (9.64)
The acceleration vector acts normal to the velocity vector and is zero if the total error is zero, or if є is parallel to uv, which never occurs. Substituting Eq. (9.63) and then Eq. (9.62) into the last equation yields
a = KV{EPuv – GEluv) = KV(UVUL0Suv – GUVUloam„) (9.65)
The two terms on the right-hand side are vector triple products (see Sec. 2.2.5.1). They convert to
![]()
a = KVlupos — uvuvuLOS — G(hloa — м„й„иша)]
We abbreviate the two terms by introducing the point guidance vector c p and the line guidance vector cl
Cp = «LOS — «i.«i)Mlos; cL — «LOA — «d«d«LOA (9-67)
and, combining it with the gravity bias term g, we obtain the three-dimensional line guidance law
a = KV{cp — Gcl) – g (9.68)
The point guidance vector generates an acceleration command that drives the missile toward the intercept point, biased toward the LOA by the line guidance vector and its gain.
The two control vectors have a geometrical interpretation. Rewriting Eq. (9.67), we recognize the plane projection tensor Nv = E — uvuv of Sec. 2.3.5:
cP=(E – «^«„Imlos = A„«los» cl=(E – «„«,.,)«loa = A. mloa (9.69)
This plane, normal to the velocity vector, is called the l a tax plane after the British designation for lateral acceleration of a missile. It contains the two control vectors, which are just the projections of the unit LOS and LOA vectors, respectively. Because both control vectors lie in the latax plane, then so does the acceleration command.
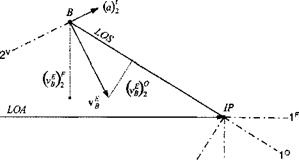
We are now ready to derive the component Eqs. (9.59) and (9.61) from the vector Eq. (9.68). To carry out our objective, we have to employ some geometry. Figure 9.27 displays the engagement of missile В against target T. For clarity, it depicts only the formation of the point guidance vector c p (the projection of the unit LOS vector «los on the latax plane). The line guidance vector would be formed by a similar projection of the unit LOA vector.
To develop the component equations, we use an alternate route to form the point guidance vector. Instead of «los> we project the unit velocity vector uv on the LOS plane and rotate the projection through the rotation tensor Rvo of the velocity frame V wrt the LOS frame О. The resultant vector is in the opposite direction of
|
|
the point guidance vector. Expressed in mathematical terms, we summarize
cP = —RV0N0uv (9.70)
where No is the planar projection tensor onto the LOS plane. This relationship is valid in any coordinate system. In particular, c p should be expressed in velocity coordinates ]v and uv in LOS coordinates ]°
[cP]v = -[Rvo}v[T}vo[No}0[uv}0 = -[N0]°[uv]° (9.71)
where [RV0]V[T]V0 = [E] [see Eq. (4.6)].
We build the line guidance vector by a similar process
cL = —RVFNFuv (9.72)
where Np is the planar projection tensor onto the plane normal to the LOA. Its component form is in velocity coordinates ]v and LOA coordinates )F
[cL]v = -[7?v’F]v'[T]v’F[Af]f [uv]F = -[AF]F[«„]F (9.73)
Substituting Eqs. (9.71) and (9.73) into Eq. (9.68) and multiplying out the matrices yields the line guidance law in component form
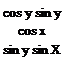 |
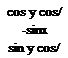 |
 |
[a]v = KV(~[N0]°[uv]° + G[NFf[uvf) – [ТУ1]#
|
( |
"о 0 о" |
‘о 0 о" |
К£)Г |
||||||
|
К |
– |
0 1 0 |
К£)2° |
+ G |
0 1 0 |
{4)1 |
|||
|
V |
0 0 1 |
К)з° |
0 0 1 |
[4)1 |
/ |
|
0 |
|||
|
К |
– g |
—sin у 0 |
|
|
К |
– (»!)? + с«)[] |
cosx |
These are Eqs. (9.59) and (9.61) and the derivation is complete.