So far we have focussed on engineering tradeoffs in an equilibrium market where the manufacturer sells the required break-even production run and the airline sells the seats w ith the average load factor. Such a model may be very useful for preliminary economic evaluation of aircraft projects. In reality however, nobody wants to sell the same product at the same pnee as their competitors. In doing so they would invariably lower the price of the product offered
The tnck is to offer something at a lower cost and higher price. This can only be done by offering something new. As an example we will discuss the introduction of a supersonic aircraft under the assumption that it does not violate any existing performance or environmental regulations
The manufacturer is now faced with two more variables: The number and pnee of the aircraft he can sell. Since he – we hope, but this is for from sure • knows what his production costs are. he would then have an idea of whether he could make a profit.
The aircraft number of units versus price is determined by a complex macro-economic model, that aircraft manufacturers such as Airbus can use as a subroutine in an ovcral aircraft optimization program.
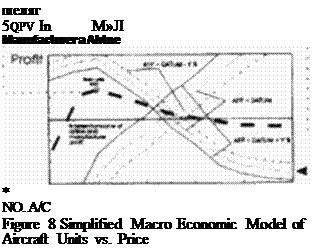
The price and number of aircraft are determined by the iteration shown in Figure 8. Its starts with an estimate of the price and number of aircraft sold. We can now use the manufacturer and airline cost models to estimate the (future) total operating cost of the aircraft

|
oKcrofT oe$Jgn
economic Mod*
|
|
Airtn# Operonna Cert Dkect rowci
Manuiocturtng Co«r lrкг» Puce Non Reewmg Cert й#си*п<3 Сол
|
For a given aircraft service (speed i passengers arc willing to pay various amounts of money on various routes. Passengers will he inclmdcd to pay more for shorter travel times. Typical business class passengers will also pay more than coach passengers, because their time is worth more. Figure К shows what fraction of passengers is willing to pay what as a function of the fare class The airline will try to sell the seats as expensive as possible So. as a function of the local route class distribution the airline will get more revenue. The airline has to sum all the revenue over all the routes an aircraft flics to decide whether to buy an individual aircraft
Ibis decision is made based on airline profit. The profit is the revenue minus the total operating cost. If the revenue of an individual aircraft purchase exceeds that of the aircraft it is replacing and there is no competing product, the manufacturer can expect to make a sale.
This ‘mixed fleet’ concept of supersonic and subsonic airliners is also shown in Figure 8 . Тік: curves shown here are typical for supersonic transports which command higher seat prices at higher operating cost than current subsonic transports
When very few aircraft arc sold, the airline is doing well. It sells all the seats of the supersonic №М$рОЛ at a premium to first class passengers. The premium is higher than the premi
um they can charge in the more competitive subsonic markets, so the airline makes more profit with this fleet mix than with a uniformly subsonic fleet. As they buy more aircraft however, more and more business class and couch class travellers fill the scats of the supersonic transport. Since the profit per supersonic coach seat is less than the profit per subsonic coach scat, the airline’s overal revenues will go down. It is obviously also true that as the manufacturer raises the price of the aircraft the airlines profit goes down too.
For the manufacturer it is another story. The more he can ask tor his aircraft the better. It is even better to sell more aircraft than to increase the purchase price As he sells more aircraft his revenues go up steeply.
The price and number of units the manufacturer can sell are determined by tlie intersection point of the airlines profit and the manufacturers profits. When the curse representing the intersection of manufacturer and airline profits goes up with the number of units, the market will keep buying the aircraft at relatively low prices. This is the case for most successful products. If the curve drops w ith the number of units, relatively few units w ill be sold at a premium. This is the case of supersonic aircraft which have a higher total operating cost than competitive subsonic transports.
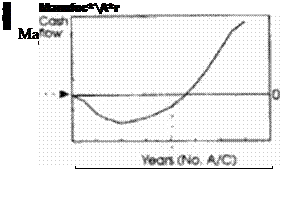
The decision to launch a supersonic transport will be determined by estimates of the manufacturers future cash flow Depending on the cost of development, the manufacturer will have to go into deep debt to finance the enterprise. Even after he starts selling the plane his negative cash flow will still increase since he will have to sell the initial planes at a discount while his actual cost – Wright curve – is much higher than the average production run.
It is therefore highly likely th3t a sealed up version of Concorde will suffer the same market fate as Concorde itself. Only when the total operating costs come down to values that arc very close to those of current subsonic transports will the projected sales be large enough to justify launching such a project. International cooperation may reduce the cash flow risk for individual companies and ameliorate this situation somewhat.
The main problem with this macroeconomic model is thai its inputs are determined by inters icw ing the custumcr (airlines), and that his views may have changed by the time the aircraft is offered for sale Therefore probability distributions have to be attributed to different scenarios.
2.4 Conclusions
The present work provides a tool to tradeoff commercial aircraft design features assuming a balanced market for subsonic and supersonic jet aircraft up to Mach 2.2. The model integrates older methods such as the ATA ’67 and the American Airlines studies of the 1980’s with newer data into one consistent whole.
Furthermore, we have presented a simplified qualitative macroeconomic model that predicts aircraft price and the number of units sold. We showed that the simplest way to sell an aircraft is to offer a product with better or equal performance than the product it is replacing at the same price or to offer the same product perfonnace at a lower price. Trading off higher performance at a higher price is highly speculative in an unknown market.
Acknowledgements
The author would like to thank Mr Schwartz, Mr Zirnmermann and Mr. Kacskc of engineering cost and market forcasting at Daimler Benz Aerospace Airbus Hamburg lor their input.
. Journal of Aeronautical sciences, feb 1936












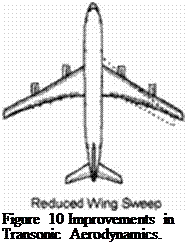 increased Wng Tmefcnaa* and Vc*jm«
increased Wng Tmefcnaa* and Vc*jm«