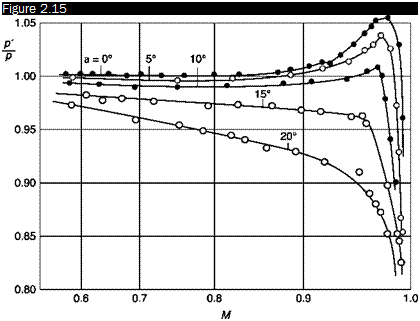
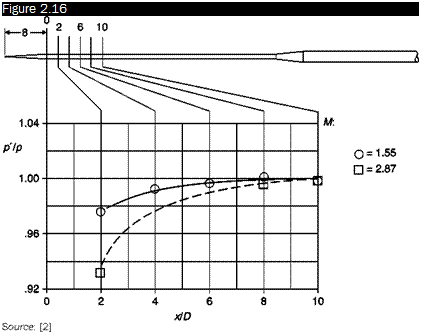
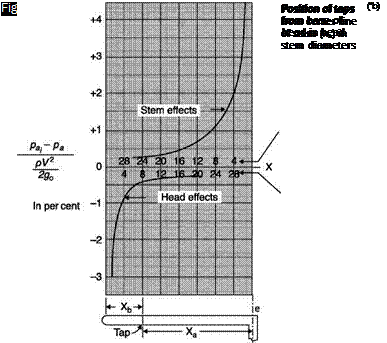
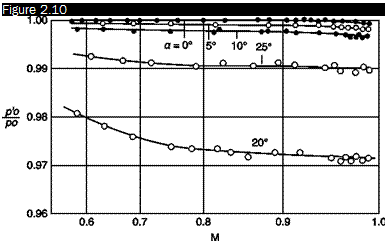
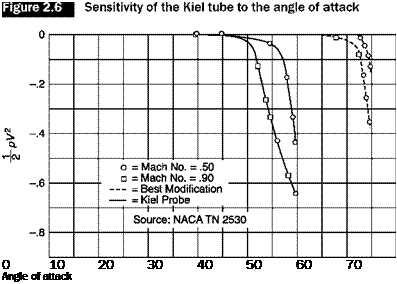
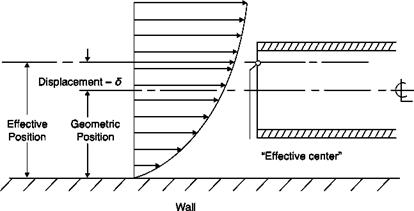
Effect of stream turbulence
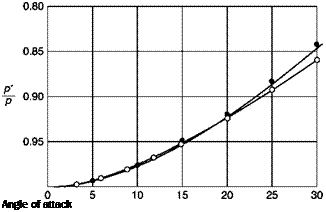
The effects of turbulence on the reading of a static tube are complex. In the case of isotropic turbulence, it is estimated that the reading error is 1% when the intensity of turbulence is 10%. There are difficulties only in the zones of separation and wakes.
2.4.2 Effect of size and shape of holes
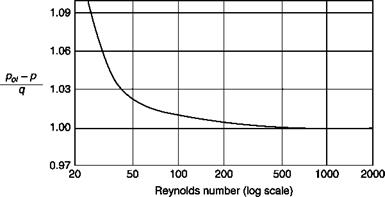
Each hole in a wall alters the boundary conditions producing a curvature of the streamlines and hence a pressure change, these effects decrease with the decreasing size of the holes. Usually the streamlines entering the
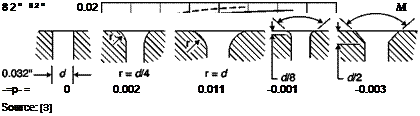
Influence of size and shape of holes on pressure readings
hole raise the pressure. In some cases the separation of the stream on the leading edge of the hole causes a decrease in pressure.
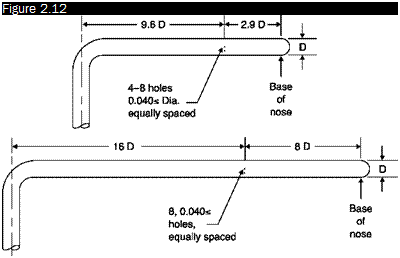
The size of the holes of static pressure must therefore be the smallest possible (see Figure 2.17, which also indicates the effect of the shape of the hole) but this is not consistent with the need not to increase excessively the inertia of the system static hole-connection pipe-pressure gage.
Typical diameters of holes in experiments at low speeds are 0.5-1 mm; in the experiments at higher speed, the size of the hole is usually chosen as the smallest that can be achieved with a power drill, e. g. 0.02 mm.