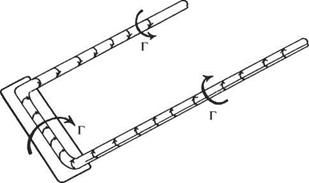
Ground effects
In this section, the influence of solid boundaries on aeroplane (or model) performance is estimated and once again the wing is replaced by the equivalent simplified horseshoe vortex.
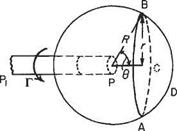
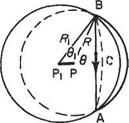
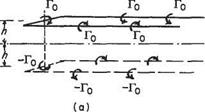
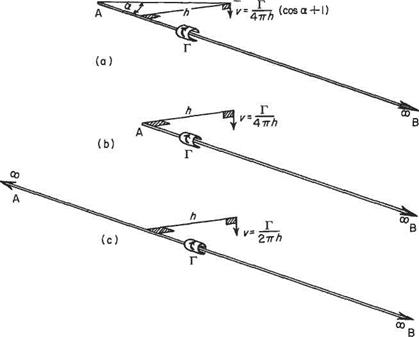
Since this is a linear problem, the method of superposition may be used in the following way. If (Fig. 5.17b) a point vortex is placed at height h above a horizontal plane, and an equal but opposite vortex is placed at depth h below the plane, the vertical velocity component induced at any point on the plane by one of the vortices is equal and opposite to that due to the other. Thus the net vertical velocity, induced at any point on the plane, is zero. This shows that the superimposition of the image vortex is equivalent in effect to the presence of a solid boundary. In exactly the same way, the effect of a solid boundary on the horseshoe vortex can be modelled by means of an image horseshoe vortex (Fig. 5.17a). In this case, the boundary is the level ground and its influence on an aircraft h above is the same as that of the ‘inverted’ aircraft flying ‘in formation’ h below the ground level (Figs 5.17a and 5.18).
Before working out a particular problem, it is clear from the figure that the image system reduces the downwash on the wing and hence the drag and power required, as well as materially changing the downwash angle at the tail and hence the overall pitching equilibrium of the aeroplane.
Example 5.2 An aeroplane of weight W and span Is is flying horizontally near the ground at altitude h and speed V. Estimate the reduction in drag due to ground effect. If W = 22 x 104N, h = 15.2m, s = 13.7m, V = 45m s-1, calculate the reduction in Newtons.
(U of L)
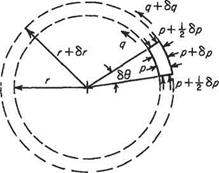
With the notation of Fig. 5.18 the change in downwash at у along the span is Aw f where
Aw t = -p-^-cos<?i – f – t——cos O2 4тггі 4лт2
On a strip of span 6y at у from the centre-line,
lift / = pVTo 6y
and change in vortex drag
* , /Aw A^= —
![]() pVToSyAw
pVToSyAw
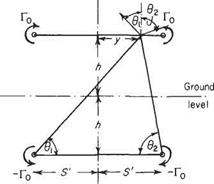
Fig. 5.18
Total change in drag AD, across the span is the integral of Eqn (5.20) from —У to s’ (or twice that from 0 to s’). Therefore
With W = рКГо7Т5 i. e. and У = (7t/4)s (assuming elliptic distribution):
AD, = 1390N
A simpler approach is to assume that mid-span conditions are typical of the whole wing. With this the case
![]() У
У
/У2 + 4h2
and the change in drag is to be 1524N (a difference of about 10% from the first answer).













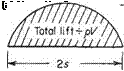

 Equating (5.2) and (5.3) gives
Equating (5.2) and (5.3) gives