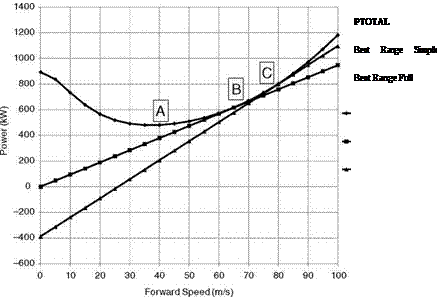
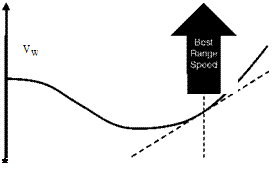
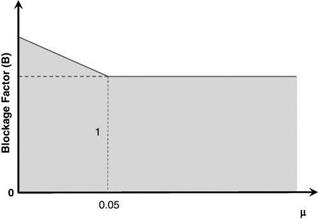
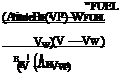Calculation Method
The calculation procedure is now presented, in schematic form, and is the basis for a flow diagram. Each part of the calculation is presented as a complete entity, in programming terms a function procedure or subroutine, with the appropriate input and output data being specified. This gives a segmented structure to the overall method, which is recommended for implementation in a computer program. The main program forms the input/output of data leaving separate routines to perform the detailed calculations.
A.7.2 Atmospheric Parameters
This determines the air parameters used by the calculations to be determined directly from the altitude and ambient temperature. An ISA atmospheric model is used. The helicopter is assumed to remain within the troposphere. Normally this is the case but in some instances helicopters have achieved very high altitudes; however these are truly exceptional and do not invalidate the model proposed.
A.7.2.1 Input
• Altitude
• Sea-level air temperature (absolute temperature at sea level)
• Sea-level air density.
A.7.2.2 Output
• Density ratio (s)
• Absolute temperature ratio (У)
• Pressure ratio (d).
A.7.2.3 Calculation
The absolute temperature ratio is given by:
y AbTmpSea Level—Altitude x LapseRate
![]() AbTmpSea Level
AbTmpSea Level
1 Altitude x LapseRate
AbTmpSea Level
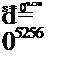 |
||
The pressure ratio by:
The lapse rate of 6.5 °C per kilometre is used in the calculations.
[1] This was a collaborative programme, jointly sponsored by Westland Helicopters and the Ministry ofDefence, which embraced blade aerofoil section research between the Royal Aircraft Establishment (now Dstl) and Westland Helicopters. This research work developed the advanced rotor blade and tip design for the Westland Lynx helicopter. Its most public achievement was the world speed record of 249.1 mph by aircraft serial number XZ170, designation G-LYNX, on 11 August 1986 over the Somerset Levels.
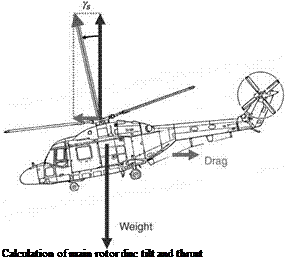
[2] Helicopter control is based primarily on directing the thrust generated by the main rotor(s). It is normally accepted that this thrust force is in a direction perpendicular to the rotor disc – that is, the plane traced out by the blade tips. This plane can be altered in two ways. The first is to alter the direction of the rotor shaft taking the rotating blades with it. The second is to permit the blades to move in a direction normal to the rotation plane, known as flapping, which allows the rotor disc plane to change without requiring any direct change in the rotor shaft. The tilting of the thrust force will in due course cause the helicopter to change its flight attitude which will then take the rotor shaft with it.
[3] = 1 (2Л0)
The thrust force is also normalized in a manner very close to that used for fixed-wing lift – that is, the product of a pressure and an area. The pressure is the dynamic pressure seen at the
[4] Autorotation is an extremely important facility because in case of a power failure the rotor can continue to produce a thrust approximately equal to the aircraft’s weight, allowing a controlled descent to ground to be made. The term ‘ideal autorotation’ is used because in practice power is still needed to overcome the drag of the blades (profile power).
[5] Some of the figures here are revisions of figures in The Foundations of Helicopter Flight by Simon Newman, Elsevier, 1994.
[6] This is seen in extreme form with the Westland Lynx world speed record helicopter (G-LYNX), see Figure 7.7.
[7] Main rotor blade tip accelerations of 750-1000g are typical.
[8] The term ‘incidence’ requires a brief reflection. In fixed-wing terminology, it is often defined as the orientation of a data line in the wing/blade relative to the forward flight direction. Helicopter aerodynamics tends to use the term ‘pitch angle’ for this orientation and reserves incidence for the inclination of the data line to the local incident flow including any downwash velocity. This is consistent with the term ‘angle of attack’. For the present discussion, incidence is the angle of the fuselage to the airflow direction generated by the motion of the aircraft.











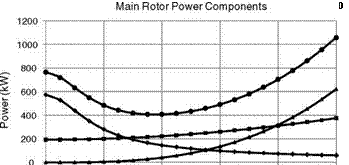
 Ф
Ф