Category BASIC HELICOPTER AERODYNAMICS

A.1 Introduction

In the main body of the book, methods have been described which enable the calculation of the power necessary to allow a helicopter to operate at a given weight and at a given speed. The results of these calculations, when combined with appropriate engine data, enable the fuel consumption to be determined and a mission can then be ‘flown’ in a computer. The ability to perform these calculations now enables a project study to be carried out on a proposed helicopter design. The purpose of this appendix is to collate the various theories of the momentum/actuator disc into an overarching calculation scheme. Earlier chapters highlighted the fact that momentum theories are the simplest available and, in order to make the results more realistic, a scheme of factoring will be required. The simplicity of these methods makes them easy to implement but, in addition, prevents them from being used for calculations where the rotor is operating close to any limitations of the flight envelope. For normal operations, this limitation should not be necessary and the simplicity of these methods will permit parametric studies to be performed with speed and economy. The modern personal computer, and the software available, make these methods, described in this appendix, readily implementable. In this way, an overall picture of the proposed helicopter configuration and its ability to complete a given mission can be readily assessed.

The following sections describe the practical use of these methods of determining the power required and the consequent rate of fuel consumption for a helicopter of given weight and speed. The calculations use the momentum method and, because of this, should only be used for a general investigation of helicopter performance. They are unsuitable for investigating helicopter performance when the aircraft is approaching its flight envelope. The methods, as presented, are formulated for a single main and tail rotor configuration. However, because of their inherent simplicity, they may readily be adapted for other rotorcraft configurations such as the tandem.

The description of the various methods is arranged in separate sections. Each section deals with a particular aspect of the helicopter.

1 Portions of this appendix have been taken from The Foundations of Helicopter Flight, by Simon Newman, Elsevier, 1994.

Basic Helicopter Aerodynamics, Third Edition. John Seddon and Simon Newman. © 2011 John Wiley & Sons, Ltd. Published 2011 by John Wiley & Sons, Ltd.

A summary of the components of the calculation is:

1. Using the helicopter’s drag and weight to determine the attitude of the main rotor disc and the thrust by balancing the force components.

2. Determination of the main rotor, induced, profile and parasite powers implementing the appropriate factors. These powers are summed to give the total power required to drive the main rotor.

3. The main rotor power is then converted to the equivalent torque which fixes the value of the tail rotor thrust necessary to trim the helicopter in yaw.

4. With the tail rotor thrust and forward speed now determined, again implementing appropriate factors, the induced and profile powers of the tail rotor can then be calculated (note: no parasite power).

5. The total helicopter power required can then be determined by summing the main and tail rotor powers together with that required to drive auxiliary services.

6. The losses in the transmission are then included as a multiplying factor which gives the power required of the engine(s).

Somebody once referred to the future thus:

There is no future – it is just the past repeating itself!

In some ways this could be applied to the evolution of rotary-wing aircraft. The tilt wing, tilt rotor, compound and stopped rotor configurations have all come and gone and come again. In some particular instances a configuration is adopted by a manufacturer who has pursued it with a continuous programme of research and development. There will be many reasons why these things happen, but the learning process must play a part. Technologies, such as electronics and computing power, allied to a constantly improving set of methods open doors previously closed to the helicopter designer/engineer. These opening doors will encourage the revisiting of the various configurations which in most cases are devoted to ways of getting past the aerodynamic speed limit of the conventional main rotor system.

Any comments on the future have to express opinions particular to the author. I do not intend to cause upset and, particularly, do not wish to tread on any sensitive toes. If, however, I provoke argument – then that is healthy. You may think me wrong, but I hope you acknowledge that my comments are expressed with the best will in the world.

What follows is the result of consulting several papers [1-3] written on areas defining where rotary-wing development can be considered.

The experience of the 1982 Falkland Islands conflict showed a level of rotary-wing operations far exceeding the operations of any other type of aircraft.

The introduction of gas-turbine propulsion systems around 1960 began the move away from piston engines. The success of these prime-movers can be attributed to several factors, namely:

• Fuel efficiency.

• Advantages in use of internal space.

• The torque transferred to the transmission was of a smoother character with fewer fluctuations.

• No clutch was required.

Basic Helicopter Aerodynamics, Third Edition. John Seddon and Simon Newman. © 2011 John Wiley & Sons, Ltd. Published 2011 by John Wiley & Sons, Ltd.

These were in spite of considerably higher speed reductions.

Then, the introduction of a rotor speed governing system, replacing the hand throttle usually placed on the collective lever control. The rotor is best served by rotating at a constant rotor speed. This is for reasons of performance but, equally importantly, to permit vibration suppression systems to have a fixed set of rotor vibration frequencies which allows vibration control to be more effective.

The use of electric power is under close scrutiny, perhaps initially for the tail rotor. The transmission can also be carefully reassessed. Gear contact is a source of wear and potential difficulties so recently research is being directed at magnetic gear contact making way for a completely new transmission layout. The skeletal gearbox was examined in the 1970s when the load bearing of the main rotor gearbox was taken from the enclosing structure to a direct line through the gear shafts themselves. There was then a rudimentary enclosure – not required to withstand the helicopter weight – which effectively kept the rain out and the lubricant in.

Automatic flight control systems (AFCSs) appeared towards the end of the 1950s. Their immediate benefit is the release of the pilot from controlling the engine throttle, thereby providing a reduction in their workload. This permits the pilot to focus on the various tasks they have to accomplish during the particular operational sortie. The initial control was provided by analogue systems known as automatic stabilization equipment (ASE) which had a relatively modest 10% authority. To this were added height and speed locks for use in cruise.

In more recent times the AFCS is now based on digital processing – albeit with a similarly limited control authority. To move on further, the control of the aircraft by such a system must earn the trust and confidence of the rotorcraft industry and operators and only then can the control system be used to mould the handling qualities of new aircraft together with new operations.

Improvements in assessing and modelling the helicopter rotor are a constant source of effort. The helicopter rotor is a very demanding place and any experiments conducted on this require a robust and accurate instrumentation system. This will need a considerable amount of computing power to process the streaming data. This computing power is also providing opportunities to investigate the aerodynamic and dynamic features of the rotor. For instance, the interaction of blades with the vortex wake can be more closely examined and the blade structural dynamic behaviour, governed by the natural modes of vibration, can be determined with more confidence and increasing detail. Modern aerodynamic modelling requires the most subtle of blade characteristics to be known. It behoves such work to establish the blade dynamic behaviour when subjected to rapidly changing aerodynamic forces if further progress is to be made. However, one must always be prepared for the unexpected, and unacceptable vibra­tion characteristics of the aircraft have caused significant disruption to helicopter develop­ment programmes.

In 1974, a programme of research into future rotor blade design was launched. It was the British Experimental Rotor Programme (BERP) and its initial designs and their children have been in existence ever since. BERP I to BERP IV trace a sequence of rotor blade developments driven by improvements in technical ability and understanding, engineering materials and manufacturing processes.

While programmes such as BERP enable rotor blade designs to be refined and reset standards for forward flight, the helicopter is still dogged by the rotor aerodynamics to pursue high-speed flight: namely, the perennial advancing/retreating-blade problem and at high speeds the requirement on the main rotor for high values of disc tilt. Rotor disc tilt will cause the fuselage to follow and with significant nose-down attitudes the attendant fuselage attitude can contribute a negative lift thereby loading the main rotor even more. Consequently, in order for a pure helicopter to be effective with a high cruise speed, the payload carried must be sacrificed for the weight of the mechanical systems at an increasing rate, particularly if the cruise speed exceeds 170 knots. This difficulty has caused designers to examine different types of rotary­wing aircraft with emphasis on two, namely the Bell Boeing V22 tilt rotor and the Piasecki compound helicopter.

Now, in the early years of the twenty-first century, what can follow?

The pure helicopter is always required to have the capability to hover efficiently, but it is also required to fly efficiently at high forward speed and to be capable of achieving extremes of endurance and range. The phrase ‘high forward speed’ is rather vague but in pure helicopter terms it is relative to the normally accepted envelope of 170 knots. So the question is posed: is 170 knots the speed limit or are we looking at a faster transit speed? The follow-up to this is the influence this high speed will have on the operating cost and efficiency of the hover.

The operation of helicopters is progressively becoming more demanding on both the aircraft and the flight crew. The demands of operating from the confines of ships’ flight decks, oil rigs or, as is becoming more prevalent, operating close to difficult terrain when visibility is poor, such as brownout, place a high requirement on sensors, so the increasing need to operate the helicopter close to the ground can avoid hazards such as cliff faces, hills, bridges and general operation in and out of cover.

It is unfortunate that the helicopter has attracted, in the past, bad publicity as regards safety of operation. This has not gone unnoticed and strenuous efforts are being made to make a helicopter as safe as possible. Indeed, airworthiness can formally prove that the helicopter is safe.

The gauntlet is thrown down to the pure helicopter to meet these challenges. There is no doubt that being able to construct new and improve existing theoretical methods will influence the design process with this knowledge and bring it to the aircraft.

The rotor blade has, pretty much so far, been a passive device. It retains its shape and only in recent years have the dynamic characteristics been used in the search for increased performance with aeroelastic tailoring. Progress now requires the consideration of active systems such as tip-jet blowing and boundary layer control. Also a considerable amount of effort is now being directed at trailing-edge morphing, where internal devices physically deform the aerofoil section. External flaps have been used for many years, but the ability to achieve these effects while avoiding an external device with its controls is seen as a step forward.

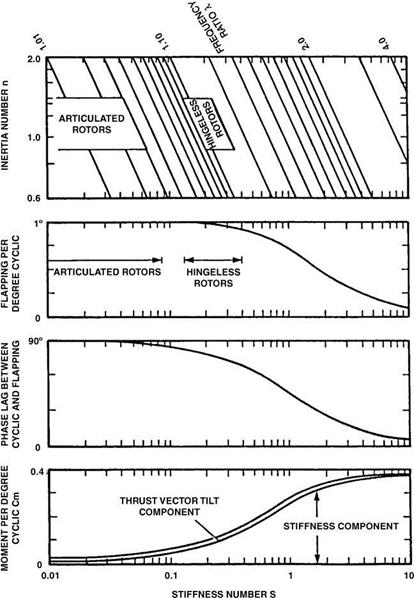
The rotor head is now increasingly using flexures rather than conventional hinges. These benefit the drag through aerodynamic cleanliness and remove a considerable burden of maintenance on the articulated rotor. A most influential benefit is the effect of a flexure system on the flight behaviour.

This naturally turns attention to the handling qualities of the helicopter. The control laws used to aid the pilot are now benefitting from the use of a greater level of embedded intelligence with the attendant ability to tailor the helicopter’s flying qualities for a particular task.

A problem with the pure helicopter has always been the method of torque control to react against the torque supplied to the main rotor and to give the pilot sufficient yaw control – usually in difficult circumstances. The open tail rotor has been used for many years, but alongside this there has been the introduction of the fenestron, the NOTAR circulation – controlled tail boom, and maybe a return to the tip-jet-driven main rotor which has no need for a specialized yaw control device.

In addition to acceptable handling qualities, the aspect of safety should be considered. In the distant past, inspections and component life were used to determine flight safety. In more recent

times, the ability of sensing systems to monitor the most critical of the helicopter components and to observe the vibration levels at different parts of the aircraft has created the Health and Usage Monitoring System (HUMS). This has improved the airworthiness levels considerably, but the future is now to use these systems to predict the degradation of a component or system so that replacement or servicing can be scheduled so that the aircraft can operate safely but the maintenance schedule will not be compromised. This is the prognostic version of HUMS. The observation of the aircraft by HUMS can provide the ability to measure fatigue giving the Fatigue and Usage Monitoring System (FUMS). All of this requires the use of the most modern and advanced electronic systems.

Or maybe new configurations will provide the way. A considerable number have been proposed or indeed flown over the years. The Sikorsky Advancing Blade Concept (ABC) of the late 1960s and early 1970s fitted to the S69 aircraft overcame the advancing/retreating-blade conflict by using a stiff coaxial rotor system which effectively relied on the advancing side of both rotors to provide the performance. Another direction was the return to the stopped rotor in the guise of the X Wing project of Sikorsky/NASA in the 1980s. It took off in the conventional way and then proceeded into forward flight under auxiliary propulsion. Use of blown blades allowed the rotor to achieve roll trim, especially as the rotor was slowed to a stop with the four – bladed rotor orientated in a 45° position giving rise to the X Wing name. The blowing sequences had to vary with blade radial position and blade azimuth making the computing effort considerable. The blades, which are normally kept in shape by the centrifugal force of rotation, are now required to support the aircraft by the structure only.

The tilt rotor concept returned and a great deal of effort was devoted to it in the 1970s, 1980s and 1990s, initially with the Bell XV-15 concept vehicle from which emerged the production version, which is the Bell Boeing V22 Osprey, now in service with the US Marine Corps – see Figure 9.1.

The tilt wing has not appeared in recent times. However, the one configuration which is seeing recent effort is the compound helicopter. The Piasecki Corporation has, for many years, worked on this type of vehicle, with particular attention paid to the tail unit providing the yaw control. By using a propeller with a cascade of vertical aerofoil louvres to deflect the downwash from the propeller in a sideways direction, the required yaw control is achieved. The louvres can be realigned so that the propeller can now act as a direct propulsion device removing this

requirement from the main rotor. The most recent application is that of a modified S-70 Blackhawk as shown in Figure 9.2.

One significant benefit of a thrust compound helicopter is that by relieving the main rotor of the need to provide propulsion, the aircraft attitude can be kept under close control. Essentially the pilot now has the ability to control both components of force rather than the main rotor supplying the vector sum. This has immediate benefits for passengers in a civil aircraft and keeping weapons on target in a military helicopter. For both variants the ability to slow to a halt can now be achieved without the attendant problem of a high nose-up attitude which can severely reduce the pilot’s view of the landing site.

The 1950s saw the development of the Fairey Rotodyne which is a compound helicopter but uses tip-jet drive in and around the hover. In forward flight it transfers to an autogyro mode whereby the power to the blade tip jets is cut off and the twin airscrews provide the necessary forward propulsion. It still holds interest – even today.

The most recent introduction to the compound helicopter stable is the Sikorsky X2 as shown in Figure 9.3.

This has a powered coaxial main rotor with a pusher propeller. On 15 September 2010 it achieved a speed of 262 knots.

Within days of the X2 achieving its high-speed record-breaking run, Eurocopter unveiled its X3 demonstrator – Figure 9.4.

This uses separate propellers mounted on stub wings either side of the main fuselage. It has a normal single main rotor. It is interesting that the idea of using forward-facing propellers to give yaw control and forward propulsion was also seen on the Fairey Gyrodyne.

A concept already mentioned is the stopped or slowed rotor. This can be seen in various developments, one being the CarterCopter which is based on the slowed rotor. A recent statement by Boeing had indicated a return to the idea of a stopped rotor. Boeing is developing a rotor that has a large thin disc at the centre of the main rotor hub. The blades are extendable/ retractable being housed within the disc. If a stopped rotor is to work it will encounter extremely large advance ratios as the rotor slows to a halt. This places a high level of difficulty on the

blades at 90° and 270° azimuth. The disc provides a safe location for the blades as the advance ratio increases beyond the normal limits.

One recent development has been the use of simulation on relatively inexpensive computer systems. It is, of course, imperative that the fidelity is of the highest quality. In the past this has required very expensive equipment; however, the quality of simulation software, which can be purchased on the high street, has improved a very great deal in the past few years and helicopter landings on ships are quite possible with inexpensive computing and software. The provision of a full moving base simulator will still be very expensive, but even that could fall to the emergence of computing power that would have been staggering only a few years ago.

The discussion has concentrated on the piloted helicopter. Rotorcraft with their unique ability to VTOL operation enable them to be considered for use as UAVs. An example is the Firescout as shown in Figure 9.5.

It is designed to operate from ships, spending in excess of 8 hours on station. It can accept a range of payloads.

So far, the discussion has been based on the Earth. In the early years of the twenty-first century, the use of a rotorcraft for exploration of the planet Mars was considered. The weight limitations are of obvious major concern but the planet has a very different atmosphere. The ‘air density’ is about 1% of that on Earth. This immediately places a very high burden on the induced power in the hover, which it will have to do as a matter of course. It will be subjected to high wind speeds and so the VTOL capability will exact its price.

In the author’s opinion, the helicopter will never replace the role of a civil fixed-wing aircraft, particularly long haul. The helicopter will supply a niche market and do it well and with increasing efficiency and safety. To ask for more is unrealistic. It will have to conform to evermore stringent regulations concerning pollution. This, of course, involves noise generation and many efforts have already been used to address this problem. An example is the scissor tail rotor of the Apache as shown in Figure 9.6.

This chapter is a discussion on what might happen. What will happen is another matter. Having worked in helicopters for 40 years now, I am very set in my ways. The baton now passes to another generation who will bring new and controversial ideas to the subject. If my 40 years have taught me anything, it is that helicopter engineers can be disruptive types who seem to specialize in asking the most awkward questions. Long may it continue!

References

1. Byham, G. M. (2003) The future of rotorcraft, Aero. J., 1072, 377-387.

2. Aiken, E. W., Ormiston, R. A., and Young, L. A. (2000) Future directions in rotorcraft technology at Ames research center, AHS 56th Annual Forum, Virginia Beach VA, May 2-4.

3. Young, L. A., Aiken, E. W., Gulick, V., Mancinelli, R., and Briggs, G. A. (2002) Rotorcraft as Mars scouts, IEEE Aerospace Conference, Big Sky, March 9-16.

In order to make the helicopter a viable operational aircraft, shortcomings in stability and control characteristics generally have to be made good by use of automatic flight control systems. The complexity of such systems, providing stability augmentation, long-term datum-holding autopilot functions, automatically executed manoeuvres and so on, depends upon the mission task, the failure survivability requirements and of course the characteristics of the basic helicopter.

Autostabilization is the response to what is perhaps the commonest situation, that in which inadequate basic stability is combined with ample control power. The helicopter is basically flyable but in the absence of automatic aids, continuous correction by the pilot would be

required – a tiring process and in some conditions (such as flying on instruments) potentially dangerous. The corrective is to utilize some of the available control power to generate moments proportional to a given motion variable and thereby correct the motion. An automatic signal is superimposed on the pilot’s manual input, without directly affecting it. No signal feeds back to the controls; the pilot merely experiences the changed flying character.

Autostabilizing systems have in the past used mechanical devices integral to the rotor; typical of these are the Bell stabilizer bar and the Lockheed control gyro (see Figure 1.30).

Alternatively, devices may be electromechanical, operating on attitude or rate signals from helicopter motion sensors. Electrical or electronic systems are the more flexible and multi­purpose. An example is the attitude hold system, which returns the helicopter always to the attitude commanded, even in disturbing environments such as gusty air. Naturally, the more the stability is augmented in this way, the greater the attention that has to be paid to augmenting the control power remaining to the pilot. The balance is often achieved by giving the pilot direct control over the attitude datum commanded. The design of a particular system is governed by the degree of augmentation desired and the total control power available.

The subject of helicopter stability and handling qualities is a very involved one and this chapter can only provide an entry point for the reader. For further information the reader is encouraged to consult dedicated texts on this subject such as Padfield as listed in Chapter 1.

References

1. Hohenemser, K. (1939) Dynamic stability of a helicopter with hinged rotor blades, NACATech. Memo. 907.

2. Sissingh, G. J. (1946) Contributions to the dynamic stability of rotary wing aircraft with articulated blades, Air Materiel Command Trans. F-TS-690-RE.

A hingeless rotor flaps in similar manner to an articulated rotor and both the rotor forces and the flapping derivatives are little different between the two. Terms expressing hub moments, however, are increased severalfold with the hingeless rotor so that, as has been said, compared with the 3% to 4% hinge offset of an articulated rotor, the effective offset of a hingeless rotor is likely to be 12% to 16% or even higher. This increased stiffness has an adverse effect on longitudinal static stability: in particular the pitch instability at high speed is much more severe (Figure 8.4). A forward CG position is an alleviating factor, but in practice the CG position is dominated by role considerations. The horizontal tailplane can be designed to play a significant part. Not only is the stabilizing influence a direct function of tailplane size, but also the angular setting to the fuselage affects the pitching moment balance in trim and can be used to minimize hub moment over the critical part of the operational flight envelope. Despite this, however, the stability degradation in high-speed flight normally remains a dominant feature.

8.5 Control

Control characteristics refer to a helicopter’s ability to respond to control inputs and so move from one flight condition to another. The inputs are made, as has been seen, by applying pitch angles to the rotor blades so as to generate the appropriate forces and moments. On the main rotor the angles are made up of the collective pitch У0 and the longitudinal and lateral cyclic pitch angles Bj and Aj as introduced in Chapter 4. The tail rotor conventionally has only collective pitch variation, determined by the thrust required for yawing moment balance.

As already introduced in Section 8.3, when the helicopter experiences a rate of pitch, the rotor blades are subjected to gyroscopic forces proportional to that rate. A nose-up rotation induces a download on an advancing blade, leading to nose-down tilt of the rotor disc. The associated offset of the thrust vector from the aircraft CG and the direct rotor moment are both in the sense opposing the helicopter rotation and constitute a damping effect or stabilizing feature. A similar argument applies to the gyroscopic effects of a rate of roll.

Adequacy of control is formally assessed in two ways, by control power and control sensitivity. Control power refers to the moment that can be generated for a given control input. It is effectively the slope of the moment v control input curve. Normalizing this in terms of aircraft moment of inertia, the measure becomes one of initial acceleration produced per unit displacement of the cyclic control stick. Control sensitivity recognizes the importance of a correlation between control power and the damping of the resultant motion – it reflects the maximum slope of the timewise response to the control input – and the ratio can be expressed as angular velocity per unit stick displacement. High control sensitivity means that control power is large relative to damping, so that a large angular velocity is reached before the damping moment stabilizes the motion.

The large effective offset of a hingeless rotor conveys both increased control power and greater inherent damping, resulting in shorter time constants and crisper response to control inputs. Basic flying characteristics in the hover and at low forward speeds are normally improved by this, because the more immediate response is valuable to the pilot for overcoming the unstable oscillatory behaviour described in Section 8.4.2. The ability of the hingeless rotor to manoeuvre the helicopter with a higher control power indicates a better path for transmitting moments and forces. This, unfortunately, causes the problem of better transmission of vibration.

A mathematical treatment of helicopter response is given by Bramwell (pp. 231-249) and illustrated by typical results for a number of different control inputs. His results for the normal acceleration produced by a sudden increase of longitudinal cyclic pitch (B1) in forward level flight at advance ratio 0.3 are reproduced in Figure 8.6. We note the more rapid response of the hingeless rotor compared with the articulated rotor, a response which the equations show to be divergent in the absence of a tailplane. Fitting a tailplane reduces the response rates and in both cases appears to stabilize them after 3 or 4 seconds.

Roll response in hover is another important flying quality, particularly in relation to manoeuvring near the ground. In an appropriate example, Bramwell shows the hingeless helicopter reaching a constant rate of roll within less than a second, while the articulated version takes 3 or 4 seconds to do so. For a given degree of cyclic pitch, the final roll rates are the same, because the control power and roll damping differ in roughly the same proportion in the two aircraft.

Rotor response characteristics can be described more or less uniquely in terms of a single non-dimensional parameter, the stiffness number S, defined as:

This expresses the ratio of elastic to aerodynamic flapping moments on the blade. Ip is the blade natural flapping frequency, having the value 1.0 for zero blade offset and related generally to the percentage offset e by:

Ip = 1 + 3e (8.2)

Thus a 4% offset yields a value Ip = 1.03; for hingeless rotors the Ip values are generally in the range 1.09 to 1.15. In Equation 8.1, n is a normalizing inertia number. Some basic rotor characteristics are shown as functions of stiffness number in Figure 8.7.

Taking the four parts of the diagram in turn, the following comments can be made.

(a) Rotors have until now made use of only relatively restricted parts of the inertia/stiffness plane.

(b) In the amount of disc tilt produced on a fixed hovering rotor per degree of cyclic pitch, articulated and the ‘softer’ hingeless rotors are practically identical.

(c) On the phase lag between cyclic pitch application and blade flapping, we observe the standard 90° for an articulated rotor with zero hinge offset (the teetering rotor), decreasing with increase of offset, real or effective, to 15°-20° lower for a hingeless rotor.

(d) For the low-stiffness numbers of articulated rotors, the principal component of moment about the aircraft CG is likely to be that produced by thrust vector tilt. Hingeless rotors, however, produce moments mainly by stiffness; their high hub moment gives good control for manoeuvring but needs to be minimized for steady flight, in order to restrict as much as possible hub load fluctuations and vibratory input to the helicopter.

In hovering flight the uncoupled longitudinal and lateral motions break down further. Longitudinal motion resolves into an uncoupled vertical velocity mode and an oscillatory mode coupling forward velocity and pitch attitude. In a similar manner, lateral motion breaks down into an uncoupled yaw mode and an oscillatory mode coupling lateral velocity and roll attitude. Both of these coupled modes are dynamically unstable. The physical nature of the longitudinal oscillation is illustrated in Figure 8.5 and can be described as follows.

Suppose the hovering helicopter was to experience a small forward velocity as at (a). This would usually be the effect of a small horizontal gust impinging on the aircraft. Incremental flapping creates a nose-up disc tilt, which results in a nose-up pitching moment on the aircraft. This is as described in Section 8.3.2 (the important overall qualification being that there is no significant aircraft drag force). A nose-up attitude develops and the backward – inclined thrust opposes the forward motion and eventually arrests it, as at (b). The disc tilt relative to the rotor shaft and hence the rotor moment have now been reduced to zero. A backward swing commences, in which the disc tilts forward, exerting a nose-down moment, as at (c). A nose-down attitude develops and the backward movement is ultimately arrested, as at (d). The helicopter then accelerates forward under the influence of the forward inclination of thrust and returns to the situation at (a). Mathematical analysis shows, and experience confirms, that the motion is dynamically unstable, the amplitude increasing steadily if the aircraft is left to itself.

This longitudinal divergent mode and its lateral-directional counterpart constitute a fundamental problem of hovering dynamics. They require constant attention by the pilot, though since both are usually of low frequency, some degree of instability can generally be allowed. It remains the situation, however, that ‘hands-off’ hovering is not possible unless a helicopter is provided with an appropriate degree of artificial stability.

8.4.1 Analytical Process

The mathematical treatment of dynamic stability given by Bramwell follows the lines of the standard treatment for fixed-wing aircraft. Wind axes are used, with the X axis parallel to the flight path, and the stability derivatives ultimately are fully non-dimensionalized. The classical format is useful because it is basic in character and displays essential comparisons prominently. The most notable distinction which emerges is that, whereas with a fixed-wing aircraft the stability quartic equation splits into two quadratics, leading to a simple physical interpretation of the motion, with the helicopter this unfortunately is not so and as a consequence the calculation of roots becomes a more complicated process.

Industrial procedures for the helicopter tend to be on rather different lines. The analysis is generally made with reference to body axes, with origin at the CG. In this way the X axis remains forward relative to the airframe, whatever the direction of flight or of relative airflow. The classical linearization of small perturbations is still applicable in principle, the necessary inclusion of initial-condition velocity components along the body axes representing only a minor complication. Force and moment contributions from the main rotor, tail rotor, airframe and fixed tail surface are collected along each body axis, as functions of flow parameters, control angles and flapping coefficients, and are then differentiated with respect to each independent variable in turn. In earlier days, computational techniques provided ready solutions to the polynomials. However, computer hardware and software have improved to an extent where many different techniques for solving the equations are possible. Full non – dimensionalization of the derivatives is less useful than for fixed-wing aircraft and a preferred alternative is to ‘normalize’ the force and moment derivatives in terms of the helicopter weight and moment of inertia respectively. This means that linear and rotational accelerations become the yardstick. These normalized terms are often referred to as concise derivatives.

In a sideslip disturbance, the rotor ‘sees’ a wind unchanged in velocity but coming from a different direction. As a result the direction of maximum flapping is rotated through the angle of sideslip change and this causes a sideways tilt of the rotor away from the wind. There is therefore a rolling moment opposing the sideslip, corresponding effectively to the dihedral action of a fixed-wing aircraft. In addition the sideslip produces a change in incidence of the tail rotor blades, so that the tail rotor acts like a vertical fin providing ‘weathercock’ stability.

8.3.3 Yawing Disturbance

A disturbance in yaw causes a change of incidence at the tail rotor and so again produces a fin damping effect, additional to that of the actual aircraft fin. Overall, however, basic directional stability tends to be poor because of degradation by upstream flow separations and wake effects.

8.3.4 General Conclusion

It is seen from the above descriptions that longitudinal static stability characteristics are significantly different from, and more complex than, those of a fixed-wing aircraft, while lateral characteristics of the two types of aircraft are similar, although the forces and moments arise in different ways.

An increase in forward speed leads to incremental flapping, resulting in a change in nose-up disc tilt. The amount of change is reckoned to be about 1° per 10m/s speed increase, independently of the flight speed. The thrust vector is effectively inclined rearwards, supported by the nose-up pitching moment produced, providing a retarding force component and therefore static stability with respect to forward speed. This characteristic is present in the hover but nevertheless contributes to a dynamic instability there (see Section 8.4.2).

An increase in speed causes the airframe drag to rise and this contributes, more effectively with initial forward speed, to a positive speed-stability characteristic for the helicopter, except in the hover.

8.3.2 Angular Velocity (Pitch or Roll Rate) Disturbance

The effect of a disturbance in angular velocity (pitch or roll) is complex. In brief, a gyroscopic moment about the flapping hinge produces a phased flapping response and the disc tilt resulting from this generates a moment opposing the particular angular motion. Thus the rotor exhibits damping in both pitch and roll. Moments arising from non-uniform incidence over the disc lead to cross-coupling, that is rolling moment due to rate of pitch and vice versa.

We consider the nature of the initial reaction to various forms of disturbance from equilibrium. Longitudinal and lateral motions are treated independently. The contributions of the rotor to forces and moments arise from two sources, variations in magnitude of the rotor force vector and variations in the inclination of this vector associated with disc tilt, which is defined by the blade flapping motion. This motion is highly dependent on hinge offset and blade Lock number – effectively the rotor control power. This is the ability to generate a moment about the rotor hub by the application of cyclic pitch and hence induce blade flapping which defines the rotor disc tilt.

8.3.1 Incidence[8] Disturbance

An upward imposed velocity (e. g. a gust) increases the incidence of all blades, giving an overall increase in thrust magnitude. Away from hover, the dissimilarity in relative airspeed on the advancing and retreating sides leads to an incremental flapping motion, which results in a nose – up tilt of the disc. Since the rotor centre lies above the aircraft CG, the pitching moment caused by the change of inclination is in a nose-up sense, that is destabilizing and increasingly so with increase of forward speed. In addition, the change in thrust magnitude itself generates a moment contribution, the effect of which depends upon the fore and aft location of the CG relative to the rotor centre. In a practical case, the thrust vector normally passes ahead of an aft CG location and behind a forward one, so the increase in thrust magnitude aggravates the destabilizing moment for an aft CG position and alleviates it for a forward one. The important characteristic therefore is a degradation of longitudinal static stability with respect to incidence, at high forward speed in combination with an aft CG position. This is also reflected in a degradation of dynamic stability under the same flight conditions. It should be noted that these fundamental arguments relate to rigid blades. With the advent of modern composite materials for blade construction, judicious exploitation of the distribution of inertial, elastic and aerodynamic loadings allows the possibility of tailoring the blade aeroelastic character­istics to alleviate the inherently destabilizing features just described.

Of the other factors contributing to static stability, the fuselage is normally destabilizing in incidence, a characteristic of all streamlined three-dimensional bodies. Hinge offset, imparting an effective stiffness, likewise aggravates the incidence instability. The one stabilizing contribution comes from the horizontal tailplane. Figure 8.4 represents the total situation

diagrammatically. The tailplane compensates for the inherent instability of the fuselage, leaving the rotor contributions as the determining factors. Of these, the stiffness effect for an articulated rotor is generally of similar magnitude to the thrust vector tilt moment. With a hingeless rotor (Section 8.5) the stiffness effect is much greater. The effect is denoted in this figure as Ma; however, this effect is normally associated with a vertical velocity perturbation and so the derivative MW is frequently used in this context.

As with a fixed-wing aircraft, both static stability and dynamic stability contribute to the flying qualities of a helicopter. Static stability refers to the initial tendency of the aircraft to return to its trimmed condition following a displacement. Dynamic stability considers the subsequent motion in time, which may consist of a dead-beat return, an oscillatory return, a no-change motion, an oscillatory divergence or a non-return divergence; the first two signify positive stability, the third neutral stability and the last two negative stability (instability). A statically unstable motion is also dynamically unstable but a statically stable motion may be either stable or unstable dynamically.

The subject of stability and control in totality is a formidable one. The part played by the rotor is highly complicated, because strictly each blade possesses its own degrees of freedom and makes an individual contribution to any disturbed motion. Fortunately, however, analysis can almost always be made satisfactorily by considering the behaviour of the rotor as a whole. Even so it is useful to make additional simplifying assumptions: those which pave the way for a classical analysis, similar to that made for fixed-wing aircraft, come essentially from the work of Hohenemser [1] and Sissingh [2] and are the following:

• in disturbed flight the accelerations are small enough not to affect the rotor response, in other words the rotor reacts in effect instantaneously to speed and angular rate changes;

• rotor speed remains constant, governed by the engine;

• longitudinal and lateral motions are uncoupled so can be treated independently. (Strictly speaking, longitudinal and lateral motions are in fact coupled. However, they can be considered uncoupled for a first analysis. Examples of situations where coupling is significant are:

– roll manoeuvres;

– lateral disc tilt induced by forward flight;

– tail rotor thrust.

Cross-coupling is present in situations such as these and has significant effects on the handling qualities.)

Given these important simplifications, the mathematics of helicopter stability and control is nevertheless heavy (Bramwell’s Chapter 7), edifying academically but hardly so otherwise, and in practice strongly dependent upon the computer for results. In this chapter we shall be content with descriptive accounts, which bring out the physical characteristics of the motions involved.

No absolute measure of stability, static or dynamic, can be stipulated for helicopters in general, because flying qualities depend on the particular blend of natural stability, control and autostabilization. Also, stability must be assessed in relation to the type of mission to be performed.