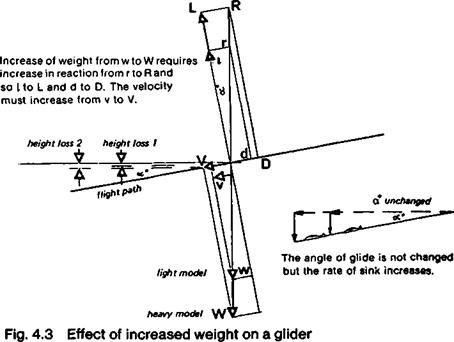
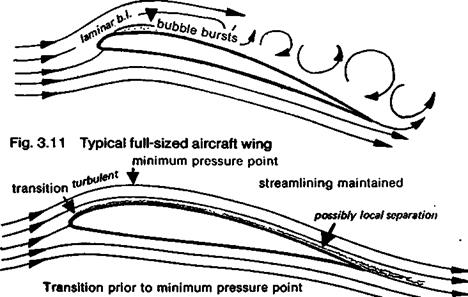
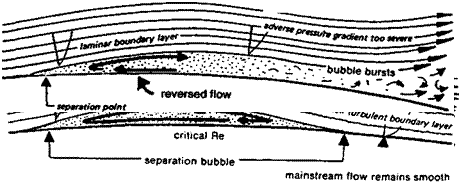
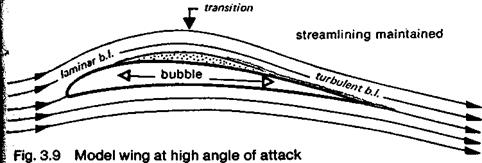
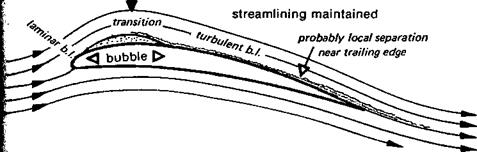
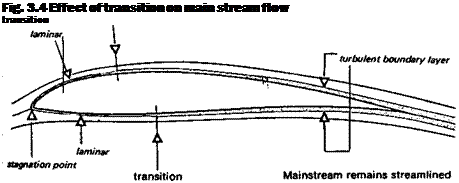
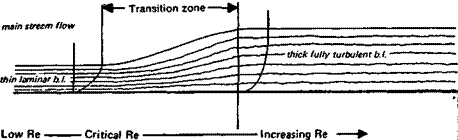
GLIDERS: THE SPEED TASK
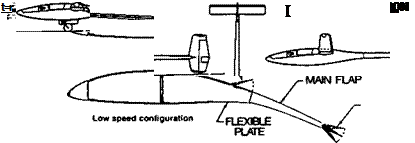
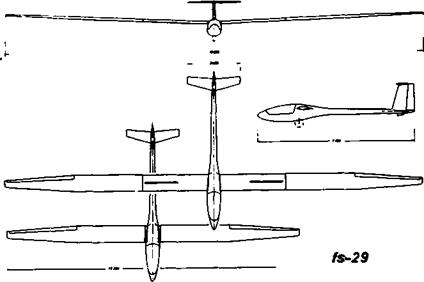
At high speeds, the R. C. glider, like the racing power model, must fly at low Cl – The wing profile, for both good penetration and soaring, is expected toproduce low drag at both high and low speeds. It should be specially designed to do this, as described in Chapter 9. In addition, the wing profile may be varied in flight by means of flaps or camber changing devices. In full-sized sailplanes both techniques are employed. The importance of wing loading is also brought out by mathematical analysis. The glider with light wing loading sinks slowly at low speed, at high speed a high wing loading improves penetration. The two conditions are incompatible unless wings of variable area can be used. Such complex devices have been employed on models and full-sized gliders. Large flaps, or even flexible, sail-like surfaces, may be extended on outriggers behind the wing (see Fig. 4.6). Apart from mechanical complications which tend to increase the weight and so to some extent defeat the purpose, the vortex-induced drag at low speeds of a broad chord is high. In terms of sinking speed, results tend to be disappointing, but when the flaps are retracted the penetration is improved greatly. Another solution, but involving much greater mechanical difficulties, is the variable span sailplane with wing extensions, either telescoping or folding. Perhaps inspired by the full-sized experimental FS-29 (Figure 4.7), Rolf Decker developed and flew a telescopic winged model sailplane in 1985. This may well prove to be successful in contests. Reliability of operation is very difficult to achieve. Models with interchangeable wings of various areas are fairly common, but while they enable adjustment to be made to conditions before each flight, there is no means of

making changes during a flight, which is the real aim. For soaring, light wing loading and low span loading are required, for penetration wing loading should be high and span loading is less significant in terms of glide ratio at speed. Such models are not permitted in the main championship classes, unless the change of geometry can be controlled remotely by radio. It is allowed to add or remove solid ballast between flights, but not to change wings. Folding wings are another possibility.