J. Merten*
Daimler-Benz Aerospace Airbus GmbH, Bremen, Germany
5.1 Introduction
In the proceeding chapters on "Son of Concorde, a Technology Challenge" and "Aerodynamic Multipoint Design Challenge" it was explained, that a well balanced contribution of new technologies in all major disciplines is required for realisation of a new Supersonic Commercial Transport (SCT). One of these technologies – usually one of the most important for aircraft – is aerodynamics. Here, the required "pure" aerodynamic technologies are specified in more detail, according to our present know ledge. Increasing insight into the problems may change the balance of importance of the individual technologies and may require some more contributions. We must never confine our knowledge to the knowledge base of an expert at a given time, but must slay open for new insights
5.2 Supersonic Flight Regime
5.2.1 Physics of supersonic flow
In air. information of small disturbances propagates at the speed of sound. This information is transported by collisions between the molecules due to molecular thermal motion building up a bumping information chain at the speed of sound At subsonic speeds, this propagation speed is faster than flight speed. Therefore, the air molecules around an aircraft are informed about the motion of the aircraft by bumping neighbouring molecules. Changes of air velocity and pressure
are therefore smooth at subsonic speeds
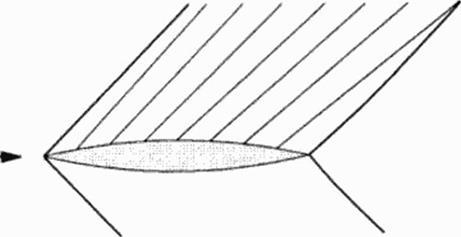
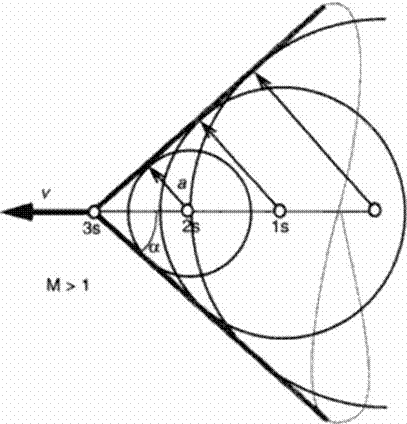
At supersonic flight speeds, the aircraft is faster than the information within the air. If we look at the disturbances produced by one small disturbance moving at supersonic speed in three succeeding seconds Figure 22. the disturbed field is inside of a cone, the Mach cone. Outside this cone, air is not yet informed about the disturbance and nobody can hear anything of it Important parameters are:
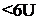
M к v/a, M Mach number
Figure 22 Mach Cone
Information is spread only within the Mach cone But the transport of individual informations from neighbouring роїш to point is even more confined. Figure 23:
|
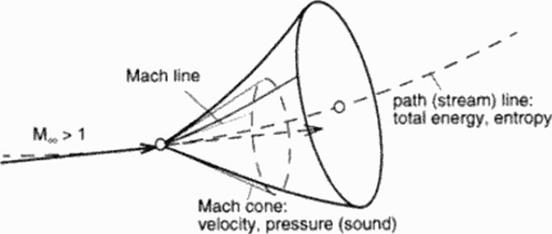
Figure 23 Propagation of Supersonic Perturbations
|
• Information about small perturbations in pressure and velocity is transferred only along Mach-lmcs in the Mach cone.
• Information about small perturbations in total energy and entropy is transferred only along tike path line or stream line (stationary flow)
The formulations above reflect at first only invite id flow without thermal conductivity. Viscous fluxes and heal conduction exist normal to the Mach cone and path (stream) line. These additional fluxes become important along the path (stream) line; along the Mach cone their influence is very low.
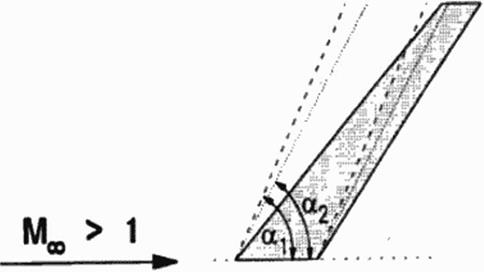
An aircraft flying ai supersonic speed is ши a small, but rather a strong perturbation. Because the air in front of the aircraft cannot be informed about the coming perturbation, smooth reaction is impossible. Instead, the air reacts instantaneously on this strong perturbation and adapts with a strong reaction to this situation: Within some free path lengths of the molecules (about 3 to 7) the airflow changes its mean velocity direction to follow the aircraft s surface. This sudden reaction not only requires a rapid flow change at the aircrafts surface, but also is radiated into the flow field. Figure 24
Air can transport information in smooth regions of the flow field only at the speed of sound. i. C. inside the Mach cone This requires that
• the Mach angle in from of the shock is smaller than the shock angle (otherwise a shock would not be needed, because smooth information would be possible);
• the Mach angle behind the shock is larger than the shock angle, because otherwise no information would be available to build up a shuck.
Speed of sound, a. only depends on temperature T:
a = у RT (63)
у: adiabatic exponent (ratio of specific heats)
R : special gas constant for air
The shock moves at supersonic speed (in normal direction to the shock surface) with respect to the air in front of the shock By passing the shock, air temperature (and speed of sound) increases to such an amount that the shock moves only at subsonic speed relative to the air behind the shock Behind strong shocks with high shock angles, the flow velocity is subsonic (relative to the aircraft), whereas for weak shocks with smaller shock angles the flow remains supersonic and only the component normal to the shock becomes subsonic. Figure 24.
|
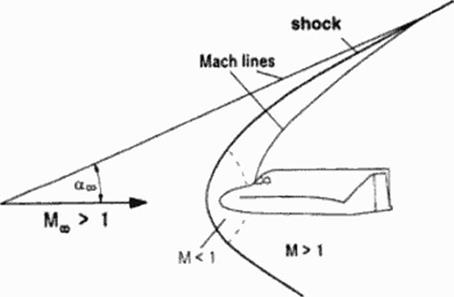
Figure 24 Strong Perturbations
|
Shock energy remains in the shock surface and is radiated only along the shock surface. Furthermore, by conflicting information from the Mach cones in front and aft the shock, new energy is radiated into the shock. Shock strength in larger distance from the aircraft therefore only very slowly decays.
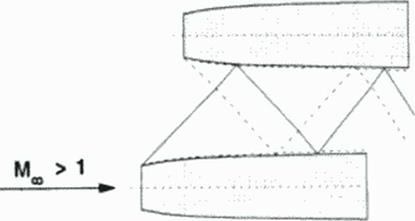
An SCT flying at about 16 000 m altitude produces a strong shock on the ground, the sonic boom Figure 25. Usually, the pressure history of the sonic boom shows two shocks: a front shock, a rear shock, and in between a nearly linear decrease of pressure, the so called N – wave. All information of wines with higher temperature concentrate at the front shock; all other informations of the regions with decreasing temperatures are collected by the rear shock. So the stable N-wave builds up and can be heard as a double bang on the ground. It is possible to design pressure distributions around the aircraft which do not steepen up to the pure N-wave. but those pressure distributions are not stable Only minor changes in temperature distribution of the air (weather conditions varying substantially in real atmosphere) or flight conditions
(Mach number; lift coefficient) destroy any carefully tuned pressure distribution and an N-wavc becomes dominant.
|
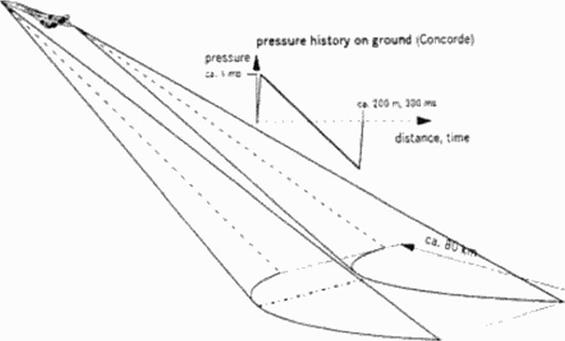
Figure 25 Sonic Boom
|
The sonic boom is always to be heard when an aircraft passes flying faster than speed of sound. The bang is the stronger tlie heavier and shorter the aircraft is. and the lower it flies. The boom carpet has a limited lateral dimension of about HO km (as the Concorde), because higher speed of sound (temperature) at low altitudes produces cutinction of disturbances This lateral carpet size strongly depends on weather (temperature distribution) and speed of the aircraft with respect to the ground. Boom strength usually is strongest about the middle of the carpet; at the side of the boom carpet, noise is lower and softer Outside the cut-off distance no bang can be heard, but – if any – only the usual aircraft noise, like a grumble.
















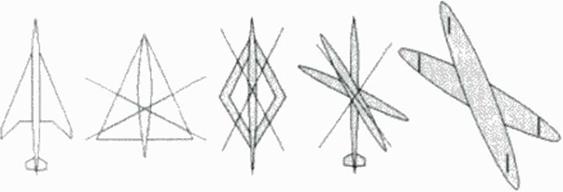
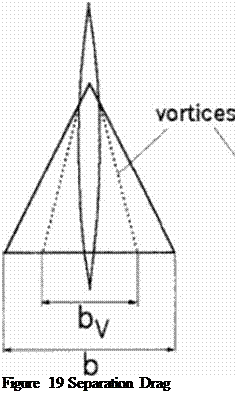 b: span for linear (potential) lift
b: span for linear (potential) lift