Helicopter rotor blades have a much lower stiffness and effective damping than the wing of a fixed wing aircraft for the in-plane (lead-lag) degree of freedom. Whereas the blade flapping and torsion degrees of freedom are primarily influenced by the lift and pitching moment respectively, the lead-lag degree of freedom is influenced by the drag. Furthermore, the blade lead-lag motion may couple with the flapping or torsion degrees of freedom and may lead to an aeroelastic instability of the blades. For example, this is intrinsic to the problem of ground resonance discussed in Section 4.10. As shown in Chapter 4, these coupling effects result from both the Coriolis forces and the aerodynamic loads. Therefore, for a comprehensive model of the rotor system it is necessary to include an accurate representation of the unsteady aerodynamic loads for all three degrees of freedom (lift, pitching moment, and drag).
For steady flow conditions, the pressure drag coefficient Cdp may be computed by resolving the normal force and axial force (or the leading edge suction force) coefficients through the AoA a using
Cdp = Cn sin a — Cacos a, (8.163)
as shown in Section 7.11.1. For steady flow the normal force coefficient is given in terms of the force curve slope, C„a(M), at a given Mach number, M, and the angle of attack, a, as
Cn = СПа{М)а. (8.164)
The corresponding axial (chord) force coefficient for these conditions is given by
Ca = СПа(М)и tana. (8.165)
where a is measured in radians. Now, it is well known that for steady potential flow the pressure drag, Cdp, is identically zero (d’Alembert’s paradox), that is,
Cdp = Cn sina—Ca cosa = C„a(M)a sina—СПа(М)а tana cosa = 0. (8.166)
However, for a real flow there is a net pressure drag on the airfoil because of viscous effects on the chordwise pressure distribution. As shown Section 7.11.1, the inability of the airfoil to attain 100% leading edge suction is modeled using the recovery factor r}a such that
Ca = Ца Cna(M)ct tana, (8.167)
where the value of rja may be adjusted empirically as necessary to give the best fit with the static axial force and/or drag measurements. Typically, the value of r)a is approximately 0.95.
The viscous (shear stress) drag is represented by the term Cj0 and is also a function of Mach number. However, its value is nominally constant for the AoA range below stall. Thus, the total drag in steady flow is given by the sum of the pressure and viscous shear components as:
Cd = Cd0 + cdp = Cdo + cn sina – Ca cosa. (8.168)
The unsteady axial force coefficient, Ca(t), depends only on the circulatory component of the loading. This is easily proved by considering the chordwise form of the circulatory and noncirculatory pressure loadings. The circulatory form is given by the standard thin-airfoil theory result, namely
The important point here is that the circulatory form has a leading edge pressure singularity, and this form of pressure distribution is obtained no matter what the value of the effective angle of attack, ae. The noncirculatory form (at time zero) is given by the piston theory result
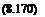 ACpC(x, t = 0) = —a.
ACpC(x, t = 0) = —a.
While this initial loading changes with time as pressure waves propagate from the airfoil, no leading edge singularity exists for any time. The general expression for the leading edge suction force is
Са = П – lim [AClx}, (8.171)
o Jc-»0 и
Thus, as a consequence of the above the unsteady axial force may be obtained directly from the steady result by replacing a by the instantaneously effective angle of attack ав +ае c/2 V, that is,
ca{t) = rja Cn(r) tanj % Г)а Cna(M) (ae + . (8.173)
Notice that the noncirculatory loading does not appear in this expression. The unsteady pressure drag (if this is required) is obtained by resolving the total normal force (including noncirculatory terms) and axial force coefficients through the AoA a to obtain
Cd(t) = C„(t) sin a – Ca(t) cos a + C^. (8.174)
See also Leishman (1987b) for further discussion on the modeling of unsteady drag.











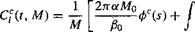 {o)fc{s-o)do, (8.199)
{o)fc{s-o)do, (8.199)

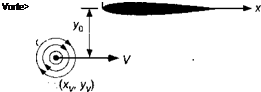
 (8.184)
(8.184)