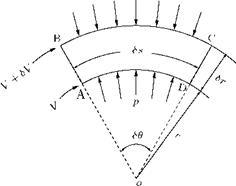
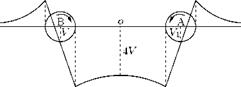
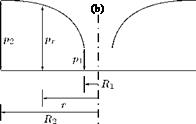
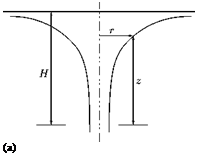
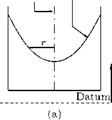
Size of a Circular Vortex
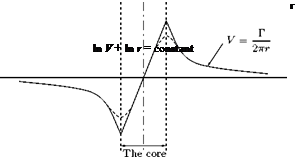
It can be shown that the pressure at the center of a circular vortex of strength y and radius a is the lowest pressure in the field of the vortex and the value is (px — yp2/a2), where px is the pressure at infinity and p is the local density. Therefore, if the pressure in the field to be positive everywhere, a2 < у 2p/pXI. That is, the radius of the vortex should be greater than or equal to у2p/p<x>. But in many occasions we are concerned with the case of a ^ 0. In such a case the resulting point vortex must be regarded as an abstraction. However, we can make a as small as we wish by making у small enough, or px large enough, but we shall still have a circular vortex and the induced velocity will be everywhere finite. The apparently infinite velocities which occur are due to the over-simplification of taking a = 0. Note that a similar lower limit is encountered for the size of a point source in two-dimensional motion, and is given by the same relation if у is taken as the strength of the source.
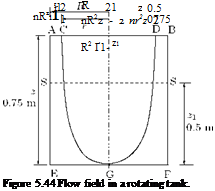
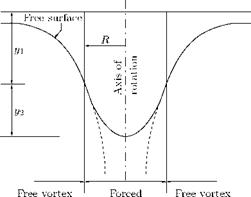
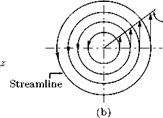
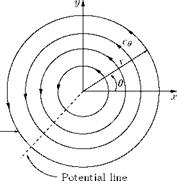
5.16 Point Rectilinear Vortex
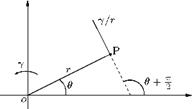
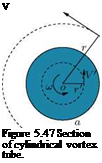
It is the limiting case of a circular vortex of constant strength у with radius a tending to zero. We have seen that any point outside a circular vortex of strength у, at distance r from the center, the velocity y/r is at right angles to r. If we let the radius a of the vortex tend to zero, the circle shrinks to a point. This limiting vortex of zero radius is called a point rectilinear vortex, or simply a point vortex of strength у. When the radius tends to zero, the cylindrical vortex tube shown in Figure 5.46 shrinks to a straight line and the vortex becomes a single rectilinear vortex represented by a point in the plane of motion, as shown in Figure 5.50.
If we take the origin at the vortex, the velocity at the point P(r, в) is represented by a complex number:
Yei(e+ 2 n) = r re—ie
We can relate this to the complex potential w = ф + as follows:
dw dw dz
dx dz dx
|
|
But z = x + iy, therefore:
![]() дф, дф дх dx u — iv.
дф, дф дх dx u — iv.
since u = дф/дх, v = —дф/дх.
Thus,
![]() u — iv
u — iv
iy iy
re‘e z
Integrating this, we get the complex potential w as:
w = iy ln z + constant
Here, the constant is irrelevant and hence can be ignored, then:
w = iy ln z
Note that the motion is irrotational except at the origin O where the vortex is positioned and so a complex potential exists, with a logarithmic singularity at the vortex.
If the vortex were at the point z0 instead of at the origin, the complex potential would be:
w = iy ln (z — z0).
It is essential to note that the velocity derived from the complex potential is the velocity induced by the vortex.












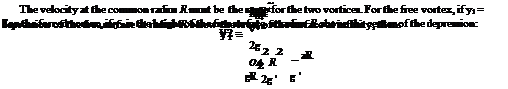
 (5.74)
(5.74)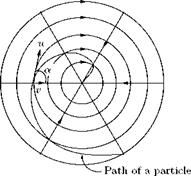

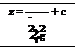
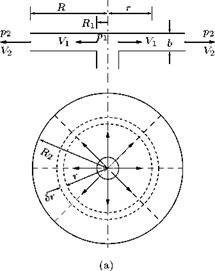
 density x area x velocity p(b x Sr)V.
density x area x velocity p(b x Sr)V.