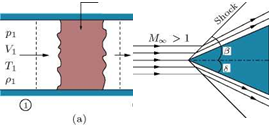
Supersonic Expansion by Turning
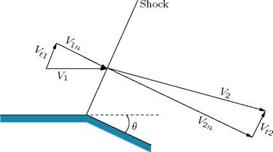
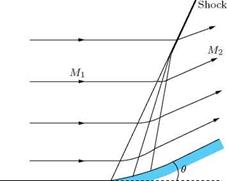
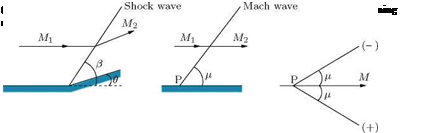
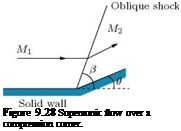
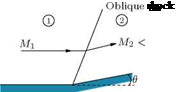
Consider the turning of a two-dimensional supersonic flow through a finite angle at a convex corner, as illustrated in Figure 9.32. Let us assume that the flow is turned by an oblique shock at the corner, as shown in the figure.
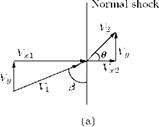
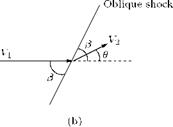
The flow turning shown in Figure 9.32 is possible only when the normal component of velocity V2n after the shock is greater than the normal component V1n ahead of the shock, since V1t and V2t on either side of the shock must be equal. Although this would satisfy the equations of motion, it would lead to a decrease of entropy across the shock. Therefore, this turning process is not physically possible. From the geometry of the flow shown in Figure 9.32, it follows that V2n must be greater than V1n. The normal momentum equation yields:
P1 + P1V12n = P2 + P2Vl – Combining this with continuity equation:
P1 V1n = P2 V2n
|
|
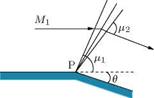
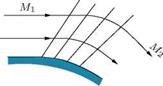
(a) Centered expansion (b) Continuous (simple) expansion
Figure 9.33 Centered and continuous expansion processes.
we obtain:
p2 p1 p1 V1n(V1n V2n) •
Because V2n > V1n, it follows that the pressure downstream of the corner should be less than the pressure upstream of the corner (p2 < p1). For this, the flow should pass through an expansion fan at the corner. Thus, the wave at the convex corner must be an expansion fan, causing the flow to accelerate. In other words, the shock wave shown at the convex corner in Figure 9.32 is a physically impossible solution.
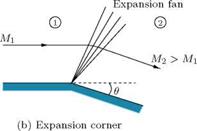
In an expansion process, the Mach lines are divergent, as shown in Figure 9.33 and, consequently, there is a tendency to decrease the pressure, density and temperature of the flow passing through them. In other words, an expansion is isentropic throughout.
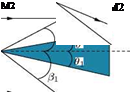
It is essential to note that the statement “expansion is isentropic throughout” is not true always. To gain an insight into the expansion process, let us examine the centered and continuous expansion processes illustrated in Figures 9.33(a) and 9.33(b). We know that the expansion rays in an expansion fan are isentropic waves across which the change of pressure, temperature, density and Mach number are small but finite. But when such small changes coalesce they can give rise to a large change. One such point where such a large change of flow properties occurs due to the amalgamation of the effect due to a large number of isentropic expansion waves is point P, which is the vertex of the centered expansion fan in Figure 9.33(a). As illustrated in Figures 9.33(a), the pressure at the wall suddenly drops from p1 to p2 at the vertex of the expansion fan. Similarly, the temperature and density also drop suddenly at point P. The Mach number at P suddenly decreases from M1 to M2. The entropy change across the vertex of the expansion fan is:
, T2 p2
S2 – St = Cp ln – R ln.
T p1
It is seen that entropy change associated with the expansion process at point p is finite. Thus, the expansion process at point P is nonisentropic. Therefore, it is essential to realize that a centered expansion process is isentropic everywhere except at the vertex of the expansion fan, where it is nonisentropic.
But for the continuous expansion illustrated in Figure 9.33(b), there is no sudden change of flow properties. Even at the wall surface the properties change gradually as shown in the figure, due to the absence of any point such as P in Figure 9.33(a), where all the expansion rays are concentrated. Therefore, the continuous expansion is isentropic everywhere.
The expansion at a corner (Figure 9.33(a)) occurs through a centered wave, defined by a “fan” of straight expansion lines. This centered wave, also called a Prandtl-Meyer expansion fan, is the counterpart, for a convex corner, of the oblique shock at a concave corner.
A typical expansion over a continuous convex turn is shown in Figure 9.33(b). Since the flow is isentropic, it is reversible.











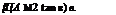 Mj2 sin2 в — 1
Mj2 sin2 в — 1


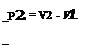
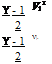


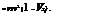 V2
V2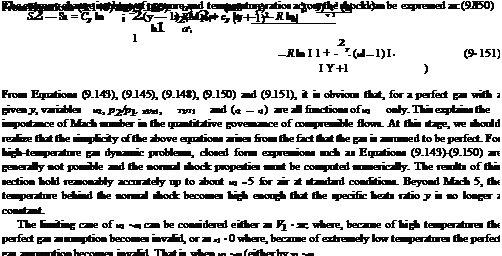
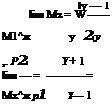 = 0.378
= 0.378