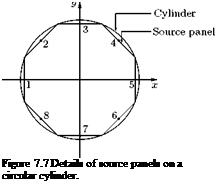
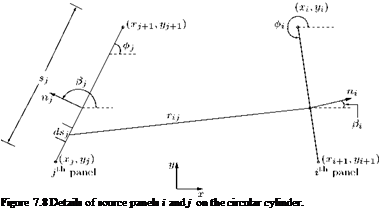
The major steps to be followed in the use of panel methods are:
• Vary the size of panels smoothly.
• Concentrate panels where the flow field and/or geometry is changing rapidly.
• Don’t spend more money and time (that is, numbers of panels) than required.
Panel placement and variation of panel size affect the quality of the solution. However, extreme sensitivity of the solution to the panel layout is an indication of an improperly posed problem. If this happens, the user should investigate the problem thoroughly. Panel methods are an aid to the aerodynamicist. We must use the results as a guide to help us and develop our own judgement. It is essential to realize that the panel method solution is an approximation of the real life problem; an idealized representation of the flow field. An understanding of aerodynamics that provides an intuitive expectation of the types of results that may be obtained, and an appreciation of how to relate your idealization to the real flow is required to get the most from the methods.
7.5.1 Limitations of Panel Method
0. Panel methods are inviscid solutions. Therefore, it is not possible to capture the viscous effects except via user “modeling” by changing the geometry.
1. Solutions are invalid as soon as the flow develops local supersonic zones [that is, Cp < CpJ. For two-dimensional isentropic flow, the exact value of Cp for critical flow is:
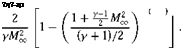 CPcri
CPcri
7.5.2 Advanced Panel Methods
So-called “higher-order” panel methods use singularity distributions that are not constant on the panel, and may also use panels which are nonplanar. Higher order methods were found to be crucial in obtaining accurate solutions for the Prandtl-Glauert Equation at supersonic speeds. At supersonic speeds, the Prandtl-Glauert equation is actually a wave equation (hyperbolic), and requires much more accurate numerical solution than the subsonic case in order to avoid pronounced errors in the solution (Magnus and Epton). However, subsonic higher order panel methods, although not as important as the supersonic flow case, have been studied in some detail. In theory, good results can be obtained using far fewer panels with higher order methods. In practice the need to resolve geometric details often leads to the need to use small panels anyway, and all the advantages of higher order panelling are not necessarily obtained. Nevertheless, since a higher order panel method may also be a new program taking advantage of many years of experience, the higher order code may still be a good candidate for use.
Example 7.1
Discuss the the main differences of panel method compared to thin aerofoil theory and compile the essence of panel method.
Solution
Although thin airfoil theory provides invaluable insights into the generation of lift, the Kutta-condition, the effect of the camber distribution on the coefficients of lift and moment, and the location of the
center of pressure and the aerodynamic center, it has several limitations that prevent its use for practical applications. Some of the primary limitations are the following:
1. It ignores the effects of the thickness distribution on lift (Cl) and mean aerodynamic chord (mac).
2. Pressure distributions tend to be inaccurate near stagnation points.
3. Aerofoils with high camber or large thickness violate the assumptions of airfoil theory, and, therefore, the prediction accuracy degrades in these situations even away from stagnation points.
To overcome the limitations of thin airfoil theory the following alternatives many be considered:
1. In addition to sources and vortices, we could use higher order solutions to Laplace’s equation that can enhance the accuracy of the approximation (doublet, quadrupoles, octupoles, etc.). This approach falls under the denomination of multipole expansions.
2. We can use the same solutions to Laplace’s equation (sources/sinks and vortices) but place them on the surface of the body of interest, and use the exact flow tangency boundary conditions without the approximations used in thin airfoil theory.
This latter method can be shown to treat a wide range of problems in applied aerodynamics, including multi-element aerofoils. It also has the advantage that it can be naturally extended to three-dimensional flows (unlike stream function or complex variable methods). The distribution of the sources/sinks and vortices on the surface of the body can be either continuous or discrete.
A continuous distribution leads to integral equations similar to those we saw in thin airfoil theory which cannot be treated analytically.
If we discretize the surface of the body into a series of segments or panels, the integral equations are transformed into an easily solvable set of simultaneous linear equations. These methods are called panel methods.
There are many choices as to how to formulate a panel method (singularity solutions, variation within a panel, singularity strength and distribution, etc.). The simplest and first truly practical method was proposed by Hess and Smith, Douglas Aircraft, in 1966. It is based on a distribution of sources and vortices on the surface of the geometry. In their method:
Ф — ф<х> + ф ф
where, ф is the total potential function and its three components are the potentials corresponding to the free stream (фот), the source distribution (ф5), and the vortex distribution (ф„). These last two distributions have potentially locally varying strengths q(s) and у(s), where s is an arc-length coordinate which spans the complete surface of the airfoil in any way we want.
The potentials created by the distribution of sources/sinks and vortices are given by:
f q(s)
Ф[11] — In ln (rds
f Y (s)
ФV — J^Vds-
Note that in these expressions, the integration is to be carried out along the complete surface of the airfoil. Using the superposition principle, any such distribution of sources/sinks and vortices satisfies Laplaces equation, but we will need to find conditions for q(s) and y(s) such that the flow tangency boundary condition and the Kutta condition are satisfied. Notice that we have multiple options. In theory:
Figure 7.10 NACA0012 aerofoil.
• Use arbitrary combinations of both sources/sinks and vortices to satisfy both boundary conditions simultaneously.
Hess and Smith made the following valid simplification:
“take the vortex strength to be constant over the whole airfoil and use the Kutta condition to fix its value, while allowing the source strength to vary from panel to panel so that, together with the constant vortex distribution, the flow tangency boundary condition is satisfied everywhere.”
Alternatives to this choice are possible and result in different types of panel methods.
Example 7.2
Calculate the pressure coefficient over an NACA0012 aerofoil with the source panel method, where the freestream attack angle is zero. Show the aerofoil shape, list the code for this, plot the source strength variation, tangential flow speed distribution over the aerofoil surface and the pressure coefficient distribution over the aerofoil.
Solution
NACA0012 profile used is shown in Figure 7.10.
The FORTRAN program to calculate the pressure distribution over an aerofoil is given below:
c source panel method
c
program spm c
integer dim parameter (dim=200) c
c*****Variables
|
c
|
num
|
number of panels
|
|
|
c
|
(xn, yn)
|
nodes
|
|
|
c
|
(xc, yc)
|
control points (mid-point of control points
|
(i) and (i+1
|
|
c
|
phi
|
panel angle
|
|
|
c
|
s
|
panel length
|
|
|
c
|
SS
|
source strength (referenced as lambda in the
|
main text)
|
|
c
|
P, Q
|
matrics and vectors s. t. [P][SS]=[Q]
|
|
|
c
|
Vinf
|
free-stream velocity
|
|
|
c
|
Vsurf
|
flow speed at control point
|
|
|
c
c
c
c
|
Cp
|
pressure coeff.
|
|
|
indx :
|
vector that records the row permutation
|
|
|
dimension xn(dim)/yn(dim)/xc(dim)/yc(dim)/phi(dim)/s(dim)
|
dimension P(dim/dim)/Q(dim)/SS(dim) dimension Vc(dim/dim)/Vsurf(dim)/Cp(dim) dimension indx(dim)
c pi=3.14………
pi = 4.0*atan(1.0) c
Vinf = 1.0 c
c******** input nodes over the surface
open(unit=50,file=’naca0012.txt’,form=’formatted’) read(50,*) num do 100 i=1,num
read(50,*) xn(i),yn(i)
100 continue c num = 8
c do 100 i=1,num
c xn(i) = cos( (180.+22.5-45.0*float(i-1))*pi/180. )
c yn(i) = sin( (180.+22.5-45.0*float(i-1))*pi/180. )
c 100 continue c
c Add an extra point to wrap back around to beginning
xn(num+1) = xn(1) yn(num+1) = yn(1) close(unit=50) c
c******** Calculate constants on each panel do 200 i=1,num
c – Set panel midpoint as control point
xc(i) = ( xn(i) + xn(i+1) ) /2.0 yc(i) = ( yn(i) + yn(i+1) ) /2.0 c – Panel length
s(i) = sqrt( (xn(i+1) – xn(i))**2 + (yn(i+1) – yn(i))**2 ) c – Panel angle
phi(i) = acos((xn(i+1) – xn(i)) / s(i)) if(yn(i+1).lt. yn(i)) phi(i)=2.0*pi-phi(i) c – Calc. vector Q
Q(i) = Vinf*sin(phi(i))
200 continue c
c******** Calculate components of matrix P do 300 j=1,num do 300 i=1,num
if (i. ne. j) then
|
– aa, bb, ..
|
. are referenced as A,
|
B, …
|
in the main text.
|
|
aa =
|
|
|
|
|
|
&
|
(-(xc(i)
|
– xn(j)
|
)*cos(phi(j)) –
|
(yc(i)
|
– yn(j))*sin(phi(j)
|
|
bb = (xc(i) – xn(j))**2 + (yc(i)
|
– yn(j
|
))**2
|
|
cc = sin(phi(i)
|
– phi(j))
|
|
|
|
dd =
|
|
|
|
|
|
&
|
(yc(i)
|
– yn(j
|
))*cos(phi(i)) –
|
– (xc(i)
|
– xn(j))*sin(phi(i
|
|
ee =
|
|
|
|
|
|
&
|
(xc(i)
|
– xn(j
|
))*sin(phi(j)) –
|
– (yc(i)
|
– yn(j))*cos(phi(j
|
|
P(i, j) =
|
(cc/2.)
|
*log((s(j)**2+2.
|
.*aa*s(j
|
)+bb)/bb)
|
|
+ (dd-aa*cc)/ee*(atan((s(j)+aa)/ee)-atan(aa/ee))
|
P(i, j) =P(i, j) / (2.0*pi)
Vc(i, j)=(dd-aa*cc)/(2.0*ee)*log((s(j)**2+2.0*aa*s(j)+bb)/bb) & – cc*(atan((s(j)+aa)/ee) – atan(aa/ee))
else
P(i, j) = 1.0/2.0 Vc(i, j)= 0.0 end if
300 continue c
c******** Find SS by solving P. SS=Q
c with LU decomposition and back-substitution
call LUdcmp(P/num/indx/d) call LUbksb(P/num/indx/Q) do 350 i=1,num SS(i) = Q(i)
350 continue c
c********Calc. Pressure coeff. do 400 i=1,num
Vsurf(i) = Vinf*cos(phi(i)) do 410 j=1,num
if (i. ne. j) Vsurf(i) = Vsurf(i) + SS(j)/(2.0*pi)*Vc(i, j) 410 continue
Cp(i) = 1.0 – (Vsurf(i)/Vinf)**2 400 continue c
c******** Results
open(unit=51,file=’result. txt’,form=’formatted’) write(51,*) ‘x y Cp SourceStrength Vsurf’ c write( 6,*) ‘x y Cp SourceStrength Vsurf’
write( 6,*) ‘x phi[deg] Cp SourceStrength/2piV Vsurf’ do 500 i=1,num
write(51,550) xc(i),yc(i),Cp(i),SS(i),Vsurf(i) c write( 6,550) xc(i),yc(i),Cp(i),SS(i),Vsurf(i)
write( 6,550) xc(i),phi(i)*180/pi, Cp(i),SS(i)/(2.*pi*Vinf)
& ,Vsurf(i)
500 continue
550 format(‘ ‘,E15.8,’ ‘,E15.8,’ ‘,E15.8,’ ‘,E15.8,’ ‘,E15.8)
stop end c c
c================================================================
c******** Subroutines
subroutine LUdcmp(a, n,indx, d) parameter(dim=200,epsln=1.0e-20) dimension indx(dim),a(dim, dim),vv(dim) c
d=1.0
c
do 100 i=1,n aamax=0.0 do 110 j=1,n
if (abs(a(i, j)) .gt. aamax) aamax = abs(a(i, j))
|
|
|
continue
if (aamax. eq.0.) then
write(6,*) ‘singular matrix in LUdcmp’ pause end if
vv(i) = 1.0 / aamax continue
do 200 j = 1,n
do 210 i=1,j-1 sum = a(i, j) do 220 k=1,i-1
sum=sum-a(i, k)*a(k, j) continue a(i, j) = sum continue aamax = 0.0 do 230 i=j, n sum = a(i, j) do 240 k=1,j-1
sum = sum – a(i, k) *a(k, j) continue a(i, j) = sum dum = vv(i) * abs(sum) if (dum. ge. aamax) then imax = i aamax = dum endif continue
if (j. ne. imax) then do 250 k=1,n
dum = a(imax, k)
a(imax, k) = a(j, k) a(j, k) = dum continue d = – d
vv(imax) = vv(j) endif
indx(j) = imax
if(a(i, j) .eq. 0.0) a(i, j) = epsln if(j. ne. n) then
dum = 1.0 / a(j, j) do 260 i=j+1,n
a(i, j) = a(i, j)*dum continue endif continue return end
|
|
|
|
|
|
|
subroutine LUbksb(a/n/indx/b) parameter(dim=200)
dimension indx(dim)/a(dim/dim)/b(dim)
|
|
c
ii = 0
do 100 i=1,n
ll = indx(i) sum = b(ll) b(ll)= b(i) if (ii. ne. 0) then do 110 j=ii, i-1
sum = sum – a(i, j)*b(j) 110 continue
else if (sum. ne. 0.0) then ii = i endif
b(i) = sum 100 continue
do 200 i=n,1,-1 sum = b(i) do 210 j=i+1,N
sum = sum – a(i, j)*b(j)
210 continue
b(i) = sum / a(i, i)
200 continue return end c
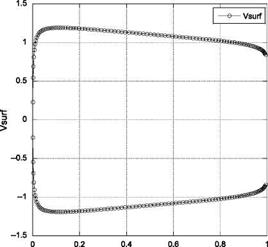
The source strength over the aerofoil surface is plotted in Figure 7.11. The tangential speed variation is shown in Figure 7.12.
The Cp distribution over the aerofoil is shown in Figure 7.13.
|

Figure 7.11 Source strength over the aerofoil.
|
|
x
Figure 7.12 Tangential speed variation over the aerofoil.
|
|
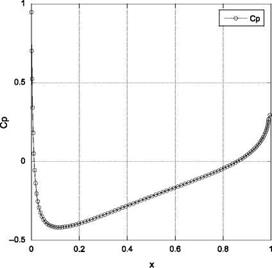
Figure 7.13 The Cp distribution over the aerofoil.
|
Example 7.3
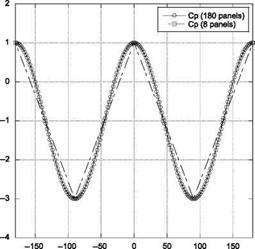
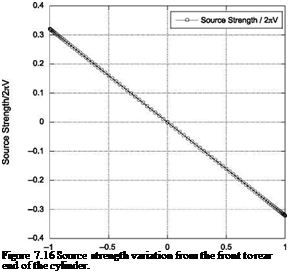
Calculate the pressure coefficient over a cylinder with unit diameter using the source panel method. List the program, compute and compare the pressure coefficient variation over the cylinder, representing it with 8 panels and with 180 panels. Also, show the source strength variation over the cylinder front to rear end.
Solution
The program in FORTRAN is given below.
c source panel method
c
program spm c
implicit none
parameter, integer (dim=200) c
c*****Variables
|
c
|
num
|
number of panels
|
|
|
c
|
(xn, yn)
|
nodes
|
|
|
c
|
(xc, yc)
|
control points (mid-point of control points
|
(i) and (i+1
|
|
c
|
phi
|
panel angle
|
|
|
c
|
s
|
panel length
|
|
|
c
|
SS
|
source strength (referenced as lambda in the
|
main text)
|
|
c
|
P, Q,SS
|
matrics and vectors s. t. [P][SS]=[Q]
|
|
|
c
|
Vinf :
|
free-stream velocity
|
|
|
c
|
Vsurf :
|
flow speed at control point
|
|
|
c
c
c
c
|
Cp
|
pressure coeff.
|
|
|
indx :
|
vector that records the row permutation
|
|
real, dimension xn(dim),yn(dim),xc(dim),yc(dim),phi(dim),s(dim) real, dimension P(dim, dim),Q(dim),SS(dim) real, dimension Vc(dim, dim),Vsurf(dim),Cp(dim) integer, dimension indx(dim)
c pi=3.14………
pi = 4.0*atan(1.0) c
Vinf = 1.0 c
c******** input nodes over the surface num = 8
do 100 i=1,num
xn(i) = cos( (-22.5+45.0*float(i-1))*pi/180. ) yn(i) = sin( (-22.5+45.0*float(i-1))*pi/180. )
100 continue c
c Add an extra point to wrap back around to beginning
xn(num+1) = xn(1) yn(num+1) = yn(1) close(unit=50)

 **** Calculate constants on each panel do 200 i=1,num
**** Calculate constants on each panel do 200 i=1,num
– Set panel midpoint as control point
xc(i) = ( xn(i) + xn(i+1) ) /2.0 yc(i) = ( yn(i) + yn(i+1) ) /2.0
– Panel length
s(i) = sqrt( (xn(i+1) – xn(i))**2 + (yn(i+1) – yn(i))**2 )
– Panel angle
phi(i) = asin((yn(i+1) – yn(i)) / s(i)) if(yn(i+1).lt. yn(i)) phi(i) = phi(i)+pi
– Calc. vector Q
Q(i) = – Vinf*sin(phi(i)) continue
**** Calculate components of matrix P do 300 j=1,num do 300 i=1,num
if (i. ne. j) then
– aa, bb, … are referenced as A, B, … in the main text. aa =
& (-(xc(i) – xn(j))*cos(phi(j)) – (yc(i) – yn(j))*sin(phi(j)))
bb = (xc(i) – xn(j))**2 + (yc(i) – yn(j))**2 cc = sin(phi(i) – phi(j))
|
&
|
dd =
(yc(i)
|
1 – yn(j))*cos(phi(i)) – (xc(i)
|
– xn(j))
|
*sin(phi(i
|
|
&
|
ee =
(xc(i)
|
1 – xn(j))*sin(phi(j)) – (yc(i)
|
– yn(j))
|
*cos(phi(j
|
|
&
|
P(i, j) = +
|
(cc/2.)*log((s(j)**2+2.*aa*s(j)+bb)/bb)
(dd-aa*cc)/ee*(atan((s(j)+aa)/ee)-atan(aa/ee))
|
|
P(i, j) =
|
P(i, j) / (2.0*pi)
|
|
|
Vc(i, j)=(dd-aa*cc)/(2.0*ee)*log((s(j)**2+2.0*aa*s(j)+bb)/bb)
& – cc*(atan((s(j)+aa)/ee) – atan(aa/ee))
else
P(i, j) = 1.0/2.0
Vc(i, j)= 0.0 end if continue
**** Find SS by solving P. SS=Q with LU decomposition call LUdcmp(P, num, indx, d) call LUbksb(P, num, indx, Q)
****Calc. Pressure coeff. do 400 i=1,num SS(i) = Q(i)
Vsurf(i) = Vinf*cos(phi(i)) do 410 j=1,num
if (i. ne. j) Vsurf(i) = Vsurf(i) + SS(i)/(2.0*pi)*Vc(i, j) continue
Cp(i) = 1.0 – (Vsurf(i)/Vinf)**2 continue
open(unit=51,file=’result. txt’,form=’formatted’) write(51,*) ‘x y Cp SourceStrength Vsurf’ write( 6,*) ‘x phi Cp SourceStrength Vsurf’ do 500 i=1,num
write(51,550) xc(i),yc(i),Cp(i),SS(i),Vsurf(i) write( 6,550) xc(i),phi(i)*180/pi, Cp(i),SS(i),Vsurf(i) 500 continue
550 format(‘ ‘,E15.8,’ ‘,E15.8,’ ‘,E15.8,’ ‘,E15.8,’ ‘,E15.8) stop end
c==============================================================
c******** Subroutines
subroutine LUdcmp(a, n,indx, d) parameter(dim=200,epsln=1.0e-20) dimension indx(dim),a(dim, dim),vv(dim) c
d=1.0
c
do 100 i=1,n aamax=0.0 do 110 j=1,n
if (abs(a(i, j)) .gt. aamax) aamax = abs(a(i, j))
110 continue
if (aamax. eq.0.) then
write(6,*) ‘singular matrix in LUdcmp’ pause end if
vv(i) = 1.0 / aamax 100 continue c
do 200 j=1,n
do 210 i=1,j-1 sum = a(i, j) do 220 k=1,i-1
sum=sum-a(i, k)*a(k, j)
220 continue
a(i, j) = sum 210 continue
aamax = 0.0 do 230 i=j, n sum = a(i, j) do 240 k=1,j-1
sum = sum – a(i, k) *a(k, j)
240 continue
a(i, j) = sum dum = vv(i) * abs(sum) if (dum. ge. aamax) then imax = i aamax = dum endif
230 continue
if (j. ne. imax) then do 250 k=1,n
dum = a(imax, k)
a(imax, k) = a(j, k) a(j, k) = dum 250 continue
d = – d
vv(imax) = vv(j) endif
indx(j) = imax
if(a(i, j) .eq. 0.0) a(i, j) = epsln if(j. ne. n) then
dum = 1.0 / a(j, j) do 260 i=j+1,n
a(i, j) = a(i, j)*dum 260 continue
endif 200 continue return end c
subroutine LUbksb(a/n/indx/b) parameter(dim=200)
dimension indx(dim)/a(dim/dim)/b(dim) c
ii = 0
do 100 i=1,n
ll = indx(i) sum = b(ll) b(ll)= b(i) if (ii. ne. 0) then do 110 j=ii, i-1
sum = sum – a(i, j)*b(j)
110 continue
else if (sum. ne. 0.0) then ii = i endif
b(i) = sum 100 continue
do 200 i=n,1,-1 sum = b(i) do 210 j=i+1,N
sum = sum – a(i, j)*b(j)
210 continue
b(i) = sum / a(i, i)
200 continue return end c
Schematic of the cylinder with 8 panels is shown in Figure 7.14.
Nondimensional pressure distribution over the cylinder, computed with 8 panels and 180 panels are compared in Figure 7.15. Variation of source strength from the front end to the rear end of the cylinder is shown in Figure 7.16.
|
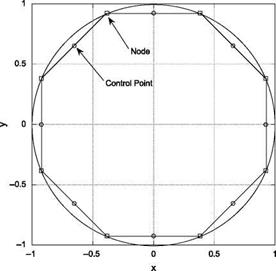
Figure 7.14 Cylinder with 8 panels.
|
|
Angle [deg]
Figure 7.15 Variation of pressure coefficient over the cylinder.
|
x
Example 7.4
Write and list the code for solving flow past a NACA0012 aerofoil, using vortex panel method. Compute and plot lift and drag coefficients and the aerodynamic efficiency for angle of attack range from — 5° to +20°.
Solution
The FORTRAN program for vortex panel method is listed below:
matrics and vectors s. t. [P][gamma]=[Q]
 free-stream velocity
free-stream velocity
angle of attack
flow speed at control point
pressure coeff.
vector that records the row permutation
dimension xn(dim)/yn(dim)/xc(dim)/yc(dim)/phi(dim)/s(dim) dimension P(dim/dim)/Q(dim)/gamma(dim) dimension Vsurf(dim),Cp(dim) dimension indx(dim)
dimension a(dim/dim)/b(dim/dim)/r(dim/dim)
 pi=3.14….
pi=3.14….
pi = 4.0*atan(1.0)
c
c – free-stream speed Vinf = 1.0
c – angle of attack (deg.) alpha = 8.0
alpha = alpha * pi/180.
c
c******** input nodes over the surface
open(unit=50,file=’naca0012.txt’,form=’formatted’) read(50,*) num do 100 i=1,num
read(50,*) xn(i),yn(i)
100 continue
c Add an extra point to wrap back around to beginning
xn(num+1) = xn(1) yn(num+1) = yn(1) close(unit=50)
c
c******** Calculate constants on each panel do 200 i=1,num
c – Set panel midpoint as control point
xc(i) = ( xn(i) + xn(i+1) ) /2.0 yc(i) = ( yn(i) + yn(i+1) ) /2.0 c – Panel length
s(i) = sqrt( (xn(i+1) – xn(i))**2 + (yn(i+1) – yn(i))**2 ) c – Panel angle
phi(i) = acos((xn(i+1) – xn(i)) / s(i)) if(yn(i+1).lt. yn(i)) phi(i)=2.0*pi-phi(i) c – Calc. vector Q
Q(i) = Vinf*sin(alpha – phi(i))
200 continue
Q(num+1) = 0.0
c
c******** Calculate components of matrix P do 300 j=1,num+1 do 300 i=1,num
r(i, j) = sqrt( (xc(i)-xn(j))**2 + (yc(i)-yn(j))**2 ) 300 continue
do 310 j=1,num
do 310 i=1,num
xcl = (xc(i)-xn(j))*cos(phi(j)) + (yc(i)-yn(j))*sin(phi(j)) ycl =-(xc(i)-xn(j))*sin(phi(j)) + (yc(i)-yn(j))*cos(phi(j))

 beta= atan(xcl/ycl) – atan((xcl-s(j))/ycl)
beta= atan(xcl/ycl) – atan((xcl-s(j))/ycl)
cc = (1./(2.*pi))*(-(1.-xcl/s(j))*log(r(i, j+1)/r(i, j))
& + (1.-ycl/s(j)*beta) )
dd = (1./(2.*pi))*( (1.-xcl/s(j))*beta & – ycl/s(j)*log(r(i, j+1)/r(i, j)) )
ee = (1./(2.*pi))*(-xcl/s(j)*log(r(i, j+1)/r(i, j))
& – (1.-ycl/s(j)*beta) )
ff = (1./(2.*pi))*( xcl/s(j)*beta
& + ycl/s(j)*log(r(i, j+1)/r(i, j)) )
a(i, j) = cc*cos(phi(i)-phi(j)) + dd*sin(phi(i)-phi(j)) b(i, j) = ee*cos(phi(i)-phi(j)) + ff*sin(phi(i)-phi(j)) continue do 320 i=1,num do 330 j=2,num
P(i, j) = a(i, j) + b(i, j-1) continue j=1
P(i,1) = a(i,1)
j=num+1
P(i, num+1)= b(i, num) continue
do 340 j=1,num+1 P(num+1,j) = 0.
if(j. eq.1.or. j.eq. num+1) P(num+1,j)=1. continue
**** Find SS by solving P. SS=Q
with LU decomposition and back-substitution call LUdcmp(P/num+1/indx/d) call LUbksb(P/num+1/indx/Q) do 350 i=1,num+1 gamma(i) = Q(i) continue
2 *log(r(i, j+1)/r(i, j))
3 + (1.0/(2.*pi))*(gamma(j+1)-gamma(j))*(1.-ycl/s(j)*beta)
dphi = phi(i)-phi(j)
Vsurf(i) = Vsurf(i) + ulocal*cos(dphi)+vlocal*sin(dphi) endif
410 continue
Cp(i) = 1.0 – (Vsurf(i)/Vinf)**2 400 continue
c
c******** Results
open(unit=51,file=’result. txt’,form=’formatted’) write(51,*) ‘x y Cp Vortex Vsurf’ write( 6,*) ‘x phi[deg] Cp Vortex Vsurf’ do 500 i=1,num
gam=(gamma(i)+gamma(i+1))/2.
write(51,550) xc(i),yc(i),Cp(i),gam, Vsurf(i)
write( 6,550) xc(i),phi(i)*180/pi, Cp(i),gam, Vsurf(i)
500 continue
550 format(‘ ‘,E15.8,’ ‘,E15.8,’ ‘,E15.8,’ ‘,E15.8,’ ‘,E15.8)
c
c******** Lift and Drag Coefficients & L/D Cx = 0.0 Cy = 0.0 do 560 i=1,num
Cx = Cx + (yn(i+1)-yn(i))*Cp(i)
Cy = Cy – (xn(i+1)-xn(i))*Cp(i)
560 continue
Cl =-Cx*sin(alpha) + Cy*cos(alpha)
Cd = Cx*cos(alpha) + Cy*sin(alpha)
write(6,*) ‘======== Aerodynamic Coefficients ========’
write(6,*) ‘Lift Coeff. = ‘,Cl write(6,*) ‘Drag Coeff. = ‘,Cd write(6,*) ‘ L/D = ‘,Cl/Cd
write(6,*) ‘==========================================’
stop
end
c=============================================================
c******** Subroutines
subroutine LUdcmp(a, n,indx, d) integer dim
parameter(dim=200,epsln=1.0e-20) dimension indx(dim),a(dim, dim),vv(dim)
c
d=1.0
c
do 100 i=1,n aamax=0.0 do 110 j=1,n
if (abs(a(i, j)) .gt. aamax) aamax = abs(a(i, j))
110 continue
if (aamax. eq.0.) then
write(6,*) ‘singular matrix in LUdcmp’ pause end if
|
vv(i) = 1.0 / aamax continue
do 200 j = 1,n
do 210 i=1,j-1 sum = a(i, j) do 220 k=1,i-1
sum=sum-a(i/k)*a(k/j) continue a(i, j) = sum continue aamax = 0.0 do 230 i=j, n sum = a(i, j) do 240 k=1,j-1
sum = sum – a(i, k) *a(k, j) continue a(i, j) = sum dum = vv(i) * abs(sum) if (dum .ge. aamax) then imax = i aamax = dum endif continue
if (j. ne. imax) then do 250 k=1,n
dum = a(imax, k)
a(imax, k) = a(j, k) a(j, k) = dum continue d = – d
vv(imax) = vv(j) endif
indx(j) = imax
if(a(i, j) .eq. 0.0) a(i, j) = epsln if(j. ne. n) then
dum = 1.0 / a(j, j) do 260 i=j+1,n
a(i, j) = a(i, j)*dum continue endif continue return end
subroutine LUbksb(a/n/indx/b) integer dim parameter(dim=200)
dimension indx(dim)/a(dim/dim)/b(dim) ii = 0
do 100 i=1,n
ll = indx(i)
= b(ll)
|
|
|
|
|
|
|
|
|
|
b(ll)= b(i) if (ii. ne. 0) then do 110 j=ii, i-1
sum = sum – a(i, j)*b(j) 110 continue
else if (sum. ne. 0.0) then ii = i endif
b(i) = sum 100 continue
do 200 i=n,1,-1 sum = b(i) do 210 j=i+1,N
sum = sum – a(i, j)*b(j)
210 continue
b(i) = sum / a(i, i)
200 continue return end
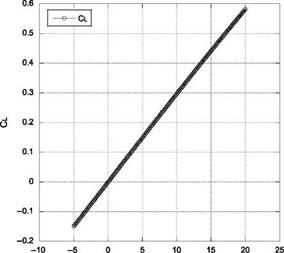
The lift and drag coefficient variation with the angle of attack for NACA0012 aerofoil, computed by vortex panel method, are shown in Figures 7.17 and 7.18, respectively. Variation of the aerodynamic efficiency of the aerofoil, calculated from the lift and drag computed with the vortex panel method, is shown in Figure 7.19.
|
Angle of Attack [deg]
Figure 7.17 Lift coefficient variation with angle of attack.
|
|
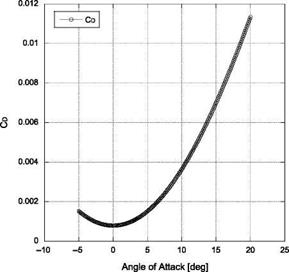
Figure 7.18 Drag coefficient variation with angle of attack.
|
|
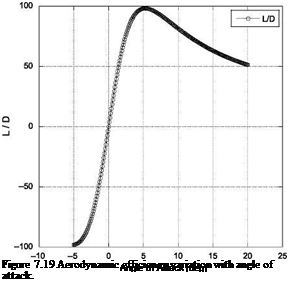 |
7.3 Summary
Panel method is a numerical technique to solve flow past bodies by replacing the body with mathematical models; consisting of source or vortex panels. These are referred to as source panel and vortex panel methods, respectively.
In general, the source strength X(s) can change from positive (+ve) to negative (—ve) along the source sheet. That is, the “source” sheet can be a combination of line sources and line sinks.
The velocity potential at point P due to all the panels can be obtained by taking the summation of the above equation over all the panels. That is:
 n
n
ф(р) = J2 Аф = J2 ln rpjds
where the distance:
rpj = J(x – Xj)2 + (y – yj)2,
where (xj, yj) are the coordinates along the surface of the jth panel.
The boundary condition is at the control points on the panels and the normal component of flow velocity is zero.
The boundary condition states that:
Vi, n + Vn =
Therefore:
|
n
Vn = 1 + £ 2n
|
dn (ln rij) dsj + Vi cos в = 0
|
|
j=1,j = i
|
‘j 1
|
This is the heart of source panel method. The values of the integral in this equation depend simply on the panel geometry, which are not the properties of the flow.
Once source strength distributions k1 are obtained, the velocity tangential to the surface at each control point can be calculated. The pressure coefficient Cp at the ith control point is:
For compressible flows the pressure coefficient becomes:
The vortex panel method is analogous to the source panel method studied earlier. The source panel method is useful only for nonlifting cases since a source has zero circulation associated with it. But vortices have circulation, and hence vortex panels can be used for lifting cases. It is once again essential to note that the vortices distributed on the panels of this numerical method are essentially free vortices.
Therefore, as in the case of source panel method, this method is also based on a fundamental solution of the Laplace equation. Thus this method is valid only for potential flows which are incompressible.
• The mid-point of each panel is a control point at which the boundary condition is applied; that is, at each control point, the normal component of flow velocity is zero.
This equation is the crux of the vortex panel method. The values of the integrals in this equation depend simply on the panel geometry; they are properties of the flow.
Pressure distribution around a body, given by source panel method is:
This is the general expression for two arbitrarily oriented panels; it is not restricted to circular cylinder only.
Exercise Problems
1. Using vortex panel method, compute and plot (a) the pressure coefficient distribution over a NACA0012 aerofoil and (b) the variation of drag coefficient with lift coefficient, for — in the range from -0.15 to 0.55, if the aerofoil is at an angle of attack of 8° in a uniform freestream.
2. List the procedure steps, along with equations, involved in the FORTRAN code vortex panel method given in Example 7.4.
3. Compute and plot the pressure coefficient variation over a NACA0012 aerofoil in a uniform freestream at angles of attack 0, 2, 5 and 8 degrees. Also plot the vortex distribution over the aerofoil profile for these angles.
Reference
1. Magnus, A. E., and Epton, M. A., “PAN AIR – A computer program for predicting subsonic or supersonic linear potential flows about arbitrary configurations using a higher order panel method”, Volume I – Theory Document (Version 1.0), NASA CR 3251, April 1980.
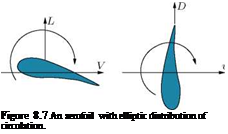
![]()
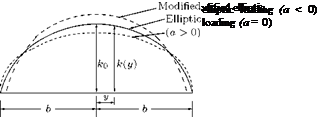
![]() C2
C2











 (8.37)
(8.37)
 k = M/1 –
k = M/1 –
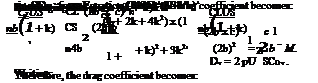

 (8.13)
(8.13)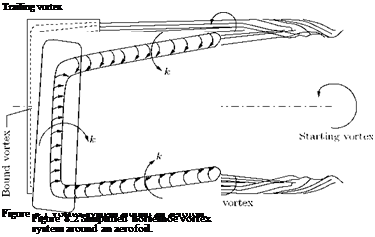
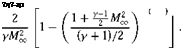 CPcri
CPcri




 free-stream velocity
free-stream velocity beta= atan(xcl/ycl) – atan((xcl-s(j))/ycl)
beta= atan(xcl/ycl) – atan((xcl-s(j))/ycl)