Materials for probes
The operation of the hot wire anemometer is based on the fact that the resistance of the wire, Rw, varies with temperature, Tw, according to the linear equation:
Rw = R[1 + a(Tw – T)] (3.1)
where Ra is the resistance at the reference temperature, Ta and а[К-1] is the temperature coefficient of the resistance.
The overheating ratio of the resistor is defined as:
Rw ~ R = a(T – T)
R w a a
The ideal material for the sensor must have a high value of a coupled with a high mechanical strength, be weldable or able to be soft soldered and reduced to wires with a very small diameter, order of pm. Table 3.1 shows the characteristics of the most used materials.
■ The tungsten wires are robust (they are used successfully in supersonic flows) and have a high temperature coefficient of resistance but cannot be used at high temperatures in air because they oxidize easily; they cannot be soldered.
■ Platinum has a good resistance to oxidation, has a good temperature coefficient, but has a low mechanical strength, especially at higher temperatures.
■ The platinum-iridium alloy is to be avoided because it is unstable at high temperatures.
■ The platinum-rhodium alloy is a compromise between tungsten and platinum, with good resistance to oxidation and strength greater than platinum, but has a low temperature coefficient.
To fix ideas about the orders of magnitudes involved, we will refer to a typical sensor consisting of a tungsten wire with length I = 1.2 mm, diameter d = 5 pm, operating temperature Tw = 300°C. Cold resistance is Ra = 3.5 W, the resistance at 300°C is Rw = 7 W, the overheating ratio = 1.












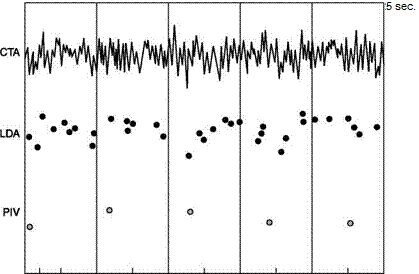

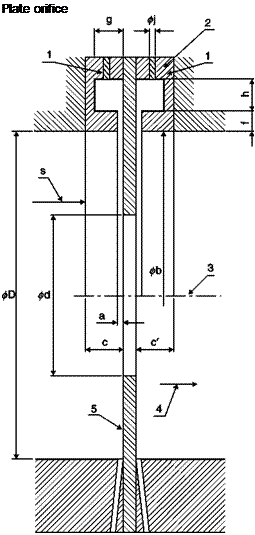
![Подпись: Mouthpiece orifice Source: [9]](/img/3131/image135_2.gif)