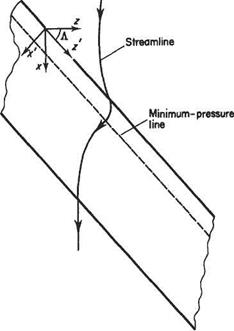
The application of the panel method described in Sections 3.5 and 4.10 above, to whole aircraft leads to additional problems and complexities. For example, it can be difficult to define the trailing edge precisely at the wing-tips and roots. In some more unconventional lifting-body configurations there may well be more widespread difficulties in identifying a trailing edge for the purposes of applying the Kutta condition. In most conventional aircraft configurations, however, it is a relatively straightforward matter to divide the aircraft into lifting and non-lifting portions – see Fig. 5.46. This allows most of the difficulties to be readily overcome and the computation of whole-aircraft aerodynamics is now routine in the aircraft industry.
In Section 4.10, the bound vorticity was modelled by means of either internal or surface vortex panels, see Fig. 4.22. Analogous methods have been used for the threedimensional wings. There are, however, certain difficulties in using vortex panels. For example, it can often be difficult to avoid violating Helmholtz’s theorem (see Section 5.2.1) when constructing vortex panelling. For this and other reasons most modern methods are based on source and doublet distributions. Such methods have a firm theoretical basis since Eqn (3.89b) can be generalized to lifting flows to read
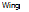
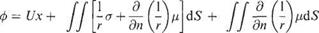 (5.81)
(5.81)
where n denotes the local normal to the surface and a and ц are the source and doublet strengths respectively.
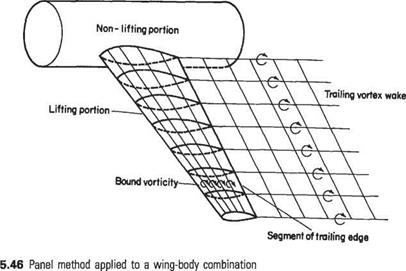
For a given application there is no unique mix of sources and doublets. For many methods[28] in common use each panel of the lifting surface is assigned a distribution of constant-strength sources. The doublet distribution must now be such that it provides one additional independent parameter for each segment of the trailing edge. Once the doublet strength is known at the trailing edge then the doublet strength on the panels comprising the trailing vortidty is determined. The initially unknown doublet strength at the trailing edge segments represents the spanwise load distribution of the wing. With this arrangement each chordwise segment of wing comprises N (say) panels and 1 trailing-edge segment. There are therefore N unknown source strengths and one unknown doublet parameter. Thus for each chordwise segment the N + 1 unknowns are determined by satisfying the N zero-normal-velocity conditions at the collocation points of the panels on the wing, plus the Kutta condition.
As in Section 4.10 the Kutta condition may be implemented either by adding an additional panel at the trailing edge or by requiring that the pressure be the same for the upper and lower panels defining the trailing edge – see Fig. 4.23. The former method is much less accurate since in the three-dimensional case the streamline leaving the trailing edge does not, in general, follow the bisector of the trailing edge. On the other hand, in the three-dimensional case equating the pressures on the two trailing-edge panels leads to a nonlinear system of equations because the pressure is related by Bernoulli equation to the square of the velocity. Nevertheless this method is still to be preferred if computational inaccuracy is to be avoided.
Exercises
1 An aeroplane weighing 73.6 kN has elliptic wings 15.23 m in span. For a speed of 90 m/s in straight and level flight at low altitude find (a) the induced drag; (b) the circulation around sections halfway along the wings. (Answer: 1.37 kN, 44m2/s)
2 A glider has wings of elliptical planform of aspect ratio 6. The total drag is given by CD = 0.02 + 0.06C|. Find the change in minimum angle of glide if the aspect ratio is increased to 10.
3 Discuss the statement that minimum induced drag of a wing is associated with elliptic loading, and plot a curve of induced drag coefficient against lift coefficient for a wing of aspect ratio 7.63.
4 Obtain an expression for the downward induced velocity behind a wing of span 2s at a point at distance у from the centre of span, the circulation around the wing at any point у being denoted by Г. If the circulation is parabolic, i. e.
calculate the value of the induced velocity w at mid-span, and compare this value with that obtained when the same lift is distributed elliptically.
5 For a wing with modified elliptic loading such that at distance у from the centre of the span, the circulation is given by where s is the semi-span, show that the downward induced velocity at у is
EofH л
4s Vl2 2s2)
Also prove that for such a wing of aspect ratio (Ад) the induced drag coefficient at lift coefficient CL is
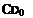 628 Cj 625 7г Ад
628 Cj 625 7г Ад
6 A rectangular, untwisted, wing of aspect ratio 3 has an aerofoil section for which the lift-curve slope is 6 in two-dimensional flow. Take the distribution of circulation across the span of a wing to be given by
Г = 4sU£A. sin (nO)
and use the general theory for wings of high aspect ratio to determine the approximate circulation distribution in terms of angle of incidence by retaining only two terms in the above expression for circulation and satisfying the equation at в = 7t/4 and тг/2.
(Answer: A = 0.372a, A2 = 0.0231a)
7 A wing of symmetrical cross-section has an elliptical planform and is twisted so that when the incidence at the centre of the span is 2° the circulation Г at a distance у from the wing root is given by
г = Го[1 – ОЛ)2]3/2
Find a general expression for the downwash velocity along the span and determine the corresponding incidence at the wing-tips. The aspect ratio is 7 and the lift-curve slope for the aerofoil section in two-dimensional flow is 5.8.
(Answer: a, iP = 0.566°)
8 A straight wing is elliptic and untwisted and is installed symmetrically in a wind – tunnel with its centre-line along the tunnel axis. If the air in the wind-tunnel has an axial velocity V and also has a small uniform angular velocity w about its axis, show that the distribution of circulation along the wing is given by
Г = 4sA 2 sin (20)
and determine Aj in terms of w and the wing parameters. (The wind-tunnel wall corrections should be ignored.)
9 The spanwise distribution of circulation along an untwisted rectangular wing of aspect ratio 5 can be written in the form:
Г = 4rva[0.023 40 sin(0) + 0.002 68 sin(30) + 0.000 72 sin(50) + 0.000 10 sin(70)]
Calculate the lift and induced drag coefficients when the incidence a measured to no lift is 10°. (Answer CL = 0.691, CD, = 0.0317)
10 An aeroplane weighing 250 kN has a span of 34 m and is flying at 40 m/s with its
tailplane level with its wings and at height 6.1m above the ground. Estimate the change due to ground effect in the downwash angle at the tailplane which is 18.3 m behind the centre of pressure of the wing. (Answer: 3.83°)
11 Three aeroplanes of the same type, having elliptical wings of an aspect ratio of 6, fly in vee formation at 67 m/s with Cl — 1.2. The followers keep a distance of one span length behind the leader and also the same distance apart from one another. Estimate the percentage saving in induced drag due to flying in this formation.
(Answer: 22%)
12 An aeroplane weighing 100 kN is 24.4 m in span. Its tailplane, which has
a symmetrical section and is located 15.2 m behind the centre of pressure of the wing, is required to exert zero pitching moment at a speed of 67 m/s. Estimate the required tail-setting angle assuming elliptic loading on the wings. (Answer: 1.97°)
13 Show that the downwash angle at the centre span of the tailplane is given to a good approximation by
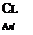 constant x
constant x
where Ar is the aspect ratio of the wing. Determine the numerical value of the constant for a tailplane located at 2s/3 behind the centre of pressure, s being the semi-span. (Answer: 0.723 for angle in radians)
14
An aeroplane weighing 100 kN has a span of 19.5m and a wing-loading of 1.925 kN/m. The wings are rather sharply tapered having around the centre of span a circulation 10% greater than that for elliptic wings of the same span and lift. Determine the downwash angle one-quarter of the span behind the centre of pressure, which is located at the quarter-chord point. The air speed is 67 m/s. Assume the trailing vorticity to be completely rolled up just behind the wings.
![]() (6.21)
(6.21)![]() (6.22)
(6.22)![]() (6.23)
(6.23)











 Tb, , 7~ 1 ma ~ UB
Tb, , 7~ 1 ma ~ UB
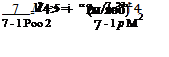
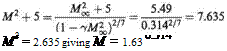


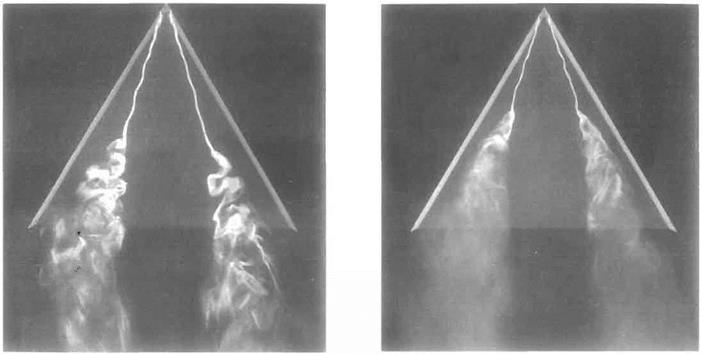
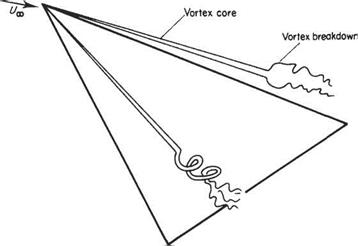
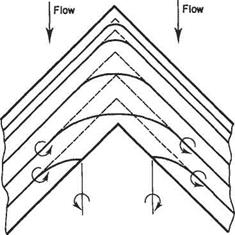
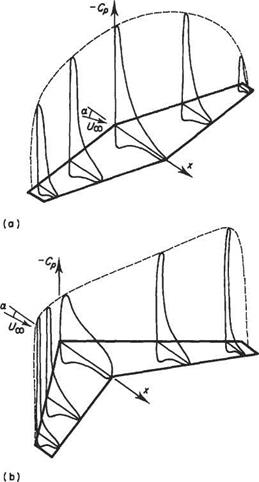

![General solution of Prandtl's integral equation Подпись: chord c = 3.048 1 J.vto — l . 3.048 (m.~« ' 5.5 — 5.8 /z [1+ 5.5 fc)J a° = 5.5 1 -^0]](/img/3130/image801_2.gif)
 ©
©