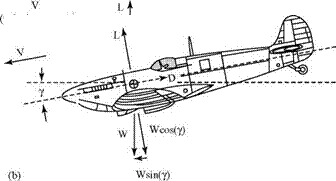
Dependence of Forces on Flow Parameters and Geometry
When designing a flight vehicle, it is necessary to clearly understand how aerodynamic forces are related to the following:
• the shape, size, and orientation of a body
• the properties of the airstream in which a body moves
Flow-field properties may include density, flight speed, and pressure. Common experience tells us that the force on a body moving through a fluid depends in some way on variables of this type.
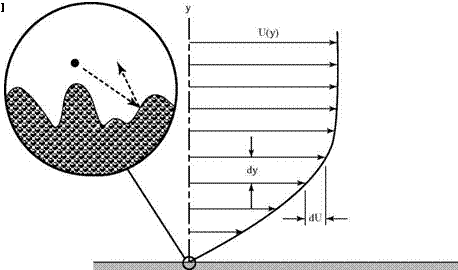
Conduct the following simple aeronautical experiment: Hold your hand out the window of a moving automobile and observe that a force can be perceived by the need to exert muscular forces to oppose those created by the airflow. Notice that if your hand is held nearly perpendicular to the air motion, there is a strong drag effect. If you hold it at a shallow angle, you feel both lift and drag. There is an obvious dependence on the orientation of your hand as well as the speed of the car, and so on. If you were to guess at the set of contributing physical variables involved based on your observations, you might choose to represent the aerodynamic force F as a mathematical function such as:
F = F (speed, density, pressure, size, shape). (2.8)
The first three variables describe the airflow; the last two indicate that the size and orientation of your hand (or another object) with respect to airflow probably affect the forces.
The basic problem of aerodynamics is defined in Chapter 1 as the determination of mathematical details of physical relationships of this type. To accomplish this, it is necessary to understand all of the important interactions of all of the participating variables and their influence on the force system. The initial difficulty is determining which of myriad possible variables matter. In the following subsections, we explore practical means to make this crucial determination.
Systems of Units
The first step is to establish precise definitions for all of the variables likely to be important. It must be possible to express each of these and their interactions in mathematical form. Of vital importance are the dimensions and associated systems of units needed to describe the variables. Such considerations likely have already had a major role in a student’s technical training, therefore, only a brief review is necessary.
A basic set of physical variables significant in aerodynamics is defined in Table 2.2. The dimensions of each property are given in terms of familiar mass-based (M, L, T) and force-based (F, L, T) systems of units. M represents mass (in kg and slugs in Systeme International [SI] and English systems of units, respectively).[2] For example, F represents the magnitude of the force (N or lbf) and t is the time in seconds.
|
Table 2.2. Important variables and fluid properties
|
|
Flow speed |
V |
V = |V|, where V is a velocity vector of gas motion at a point in the flow |
‘ L’ T |
" L’ T |
|
|
Sound speed |
a |
Speed of propagation of weak disturbances; a measure of compressibility effects |
‘ L’ T |
" L’ T |
|
|
Acceleration |
dV dt |
Local rate of change of speed of gas particles; proportional to forces acting on particles |
" L ‘ T2 _ |
L ‘ T2 _ |
|
|
Force |
F |
Force due to interaction of a gas flow with an object |
ML T 2 |
[F] |
|
|
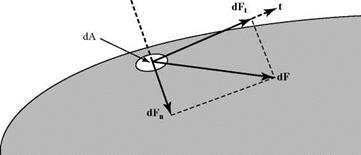
Pressure |
P |
Г f dF Л Г |
M |
П |
Г F ] |
|
(or normal stress) |
P = hm 1 dA 1, where dA ^ 0V y L dF is the force on the surface element dA; force per unit area normal to a reference surface |
LT2 |
. L2 _ |
||
|
Shear stress |
T |
Force per unit area parallel Г to a reference surface |
M LT2 |
‘ F ‘ . L2 _ |
|
|
Density |
p |
p = lim f 1, where dv ^ 0 ^ dV ) dm is mass contained within the volume element, dV |
" M’ _ L3 _ |
FT2 L4 |
|
|
* Metric SI units are |
based on |
length, L; time, T; and mass, M. Force is a derived unit. |
|
і Traditional English engineering units are based on length, L; time, T; and force, F. Mass is a derived unit. |
For the most part, these are familiar thermodynamic variables; therefore, only a brief review is necessary. Other variables may be needed to describe the fundamental characteristics of a flowing liquid or a gas. They are defined by basic physical relationships; they are sometimes empirical in nature, requiring knowledge of experimentally determined parameters. For example, in the case of an ideal gas, the thermodynamic variables are related by the familiar gas law, sometimes called the equation of state or constitutive equation, expressed in Eq. 2.1. The gas constant, R = WM, that appears in this equation is known from extensive experimental studies and from statistical mechanics and the kinetic theory of gases. ^ is the universal gas constant and M is the molecular weight.
![]() Similarly, forces and acceleration of gas particles are related by Newton’s Second Law of Motion, so that (from the point of view of physical dimensions) for a gas particle of mass m, we write:
Similarly, forces and acceleration of gas particles are related by Newton’s Second Law of Motion, so that (from the point of view of physical dimensions) for a gas particle of mass m, we write:
dV
F = m—V. (2.9)
dt
If we must account for viscous stresses, t, we need to know that a relationship of the type deduced in Eq. 2.4 might be involved. Table 2.2 illustrates how the correct dimensions for possibly unfamiliar physical variables such as the coefficient of viscosity, p, in Eq. 2.4 can be determined by means of the principle of dimensional homogeneity. For Eqs. 2.4 and 2.9 to be correct, the dimensions of quantities represented on the left and right sides of the equation must be identical.
EXAMPLE 2.1 Required: Verify the dimensions of force in a mass-based system of units as listed in Table 2.2. Determine the corresponding standard metric SI and English engineering units for force.
Approach: Use the principle of dimensional homogeneity and Newton’s Second Law (Eq. 2.9).
Solution: The defining equation and the corresponding dimensions are:
dV
m——
where the brackets denote dimensions of the enclosed variable.
Discussion: Often, the symbols denoting basic units are the same as those appearing in the defining equation. Here, the symbols for generic mass, m, and time, t, are the same as the corresponding quantities in Newton’s Second Law.
From this, it is clear that 1 unit of force in the SI system is expressed (in mass-based units) as:
„kg m „
1 &. =1 newton
s2
because mass is measured in kilograms, length in meters, and time in seconds. Similarly, 1 unit of force in the English engineering system is:
iSuS^.nbf
sec2
because the basic unit of mass is the slug in English units. The most common abbreviations for various quantities are used.
EXAMPLE 2.2 Required: Find the weight of an object with a mass of 1 slug at the earth’s surface.
Approach: Use Newton’s Second Law in English engineering units.
Solution: Because the acceleration due to gravity at the earth’s surface is approximately 32.17 ft/sec2, the gravitational force (i. e., the weight) is:
W = 1 slug x 32.17 ft/sec2 = 32.17 lbf.
Discussion: It is useful to use the abbreviation Ibf to denote forces to distinguish between two common uses for the pound (Zb). The pound-mass (lbm) often is used in some technical fields: 1 Ibm is the amount of mass that would weigh 1 pound at the earth’s surface. In compatible units, this is equivalent to 1/32.17 ~ 0.031 slug. At the earth’s surface, the weight of an object with a mass of 1 slug is about 32.17 lbf.
Notice that English units are a force-based system using the pound as the basic unit. However, Newton’s Second Law (Eq. 2.9) indicates that 1 lbf can be written as:
Notice that this defines the mass unit that is compatible with the chosen units for acceleration. It is incorrect to replace slug with lbm because, by definition, 1 lbm is the mass that weighs 1 lbf at the earth’s surface.
Of course, equations can be written that contain the conversion factors needed to adjust the units. In some fields of study (e. g., thermodynamics and heat transfer), it is traditional to use lbm as the mass unit when working in English engineering units. It is then necessary to insert the factor go = 32.17 lbm/slug in any numerical calculations.
It is better to use compatible units so that serious numerical errors can be avoided. It was once common practice in engineering textbooks to display constants such as go or J (i. e., the number of ft-lb/sec per BTU) in the fundamental equations to remind users to adjust the units. This is not done in this book! Dimensional numerical constants should not appear in the fundamental equations. It is necessary to check dimensional homogeneity only to be sure that the correct units are applied to represent each variable involved.
EXAMPLE 2.3 Required: Find the dimensions of the coefficient of viscosity using Newton’s Viscous Force Law (Eq. 2.4). Then, determine the corresponding units in standard SI and English units.
Approach: Use the principle of dimensional homogeneity.
Solution: From Table 2.2, the shearing stress (i. e., force per unit area) in mass – based units has the following dimensions:
[t]=[ml/ t2 ]/[l2 ]=[m/lt2 ],
and the dimensions of the velocity gradient are:
3u
0y
Then, for dimensional homogeneity, the correct dimensions for the viscosity coefficient must be:
M
LT ‘
Thus, in the SI system, the viscosity coefficient must have kg/m-sec units. In the force-based engineering system, the units are lbf sec/ft2.
The application of Newton’s Second Law shows that viscosity also can be written in terms of the units slug/ft sec. By similar reasoning, it is correct to write the viscosity coefficient with N-s/m2 units.