Thrust Approximations
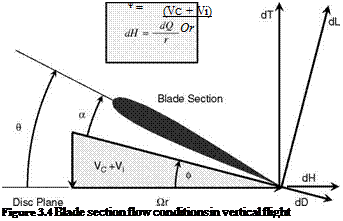
If the blade incidence a is measured from the no-lift line and stall and compressibility effects can be neglected, the section lift coefficient can be approximated by the linear relation:
![]() Cl = aa = а(в—ф)
Cl = aa = а(в—ф)
where the two-dimensional lift slope factor a has a value of about 5.7. Analyses of potential flow by Glauert [1] give a value for the lift curve slope of 2p per radian. The value of 5.7 is more representative allowing for losses due to viscous effects. This value also has the added benefit of being equivalent to 0.1 per degree. Equation 3.18 then takes the form:
![]()
|
|
|
|
|
|
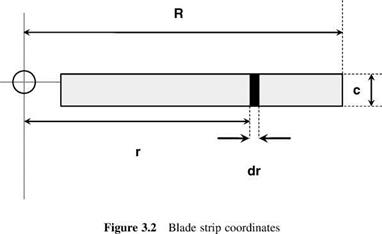
![]() (вх2—lx) dx
(вх2—lx) dx
For a blade of zero twist, в is constant. For uniform induced velocity – as assumed in simple momentum theory – the inflow factor l is also constant. In these circumstances Equation 3.26 integrates readily to:
|
|||
|
|||
|
|
||
Conventionally, modern blades incorporate negative twist, decreasing the pitch angle towards the tip with the objective of evening out the blade loading distribution. Thus в takes a form such as:
в = во-кх (3.28)
Here, к is a linear twist expressed over the entire blade from rotor centre to blade tip. Modern blades can have twist variations which are nonlinear. Using this form, the thrust coefficient becomes:
The first two terms can be combined by introducing the blade pitch angle at 75% radius:
so the thrust coefficient becomes:
and the relation in Equation 3.27 is restored.
Thus a blade with linear twist has the same thrust coefficient as one of constant в equal to that of a linearly twisted blade at three-quarters radius.
Equation 3.27 expresses the rotor thrust coefficient as a function of pitch angle and inflow ratio. For a direct relationship between thrust coefficient and pitch setting, we need to remove the l term. This can be achieved by recalling the link between thrust and induced velocity provided by the momentum theorem.
For the rotor in hover, this is Equation 2.12, which on incorporation with Equation 3.27 leads to:
in which for a blade with a linear twist, в is taken at three-quarters radius. It is readily seen that correspondingly the direct relationship between в and l is:
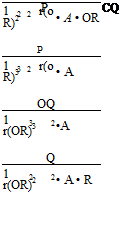
![]() (3.33)
(3.33)











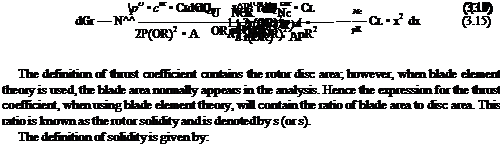
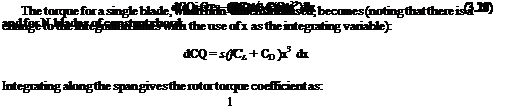




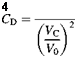 (2.63)
(2.63)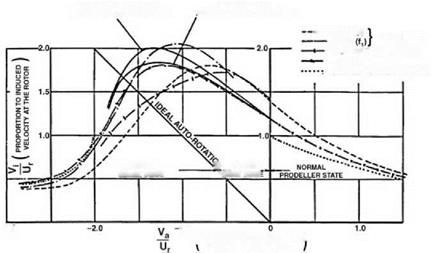
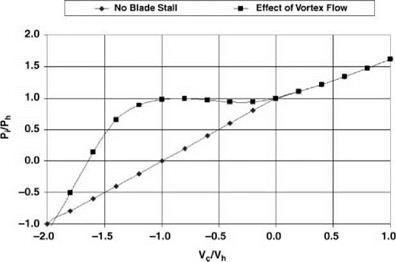
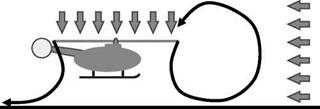
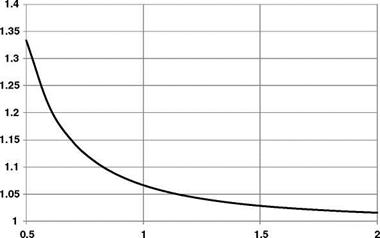
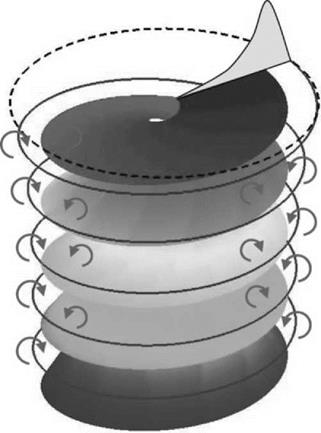
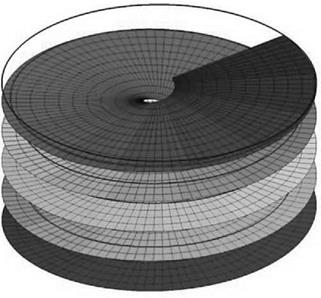
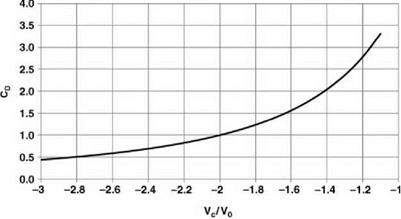
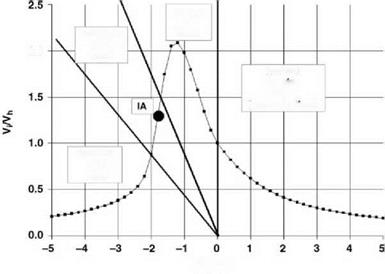 This is shown in Figure 2.22, using the simple momentum theory results of Equation 2.55 in the regions to which they apply. We see that on moving from hover into descent the induced velocity increases more rapidly than momentum theory would indicate. The value rises, in the vortex ring state, to about twice the hover value, then falls steeply to about the hover value at entry to the windmill brake state.
This is shown in Figure 2.22, using the simple momentum theory results of Equation 2.55 in the regions to which they apply. We see that on moving from hover into descent the induced velocity increases more rapidly than momentum theory would indicate. The value rises, in the vortex ring state, to about twice the hover value, then falls steeply to about the hover value at entry to the windmill brake state.