For engineering applications, sometimes it is sufficient to compute the mean velocity profile of a turbulent flow. For this purpose, it has been recognized that the effect of turbulence on the mean flow may be adequately accounted for by including a turbulence-induced stress field. This is the Boussinesq approach. In this approach, the stress field is modeled by relating it to the strain rate field of the mean flow similar to that of laminar flow. This turbulence modeling approach is simple and relatively easy to implement on a computer. For this reason, it has become a wildly popular tool for solving practical problems for which only the mean flow is required.
Turbulence modeling is by now a well-established subject. An in-depth discussion of turbulence modeling is beyond the scope of this book. The objective here is to provide an introductory presentation of the subject. There are two most popular two-equation turbulence models. They are the к – є model and the к – ю model (Wilcox, 1998). A one-equation model by Spalart and Allmaras (1994) is also often used. It is now known that the к – є model works well for free shear turbulent flows, while the к – ю model works well for turbulent fluid layers adjacent to a solid surface. Motivated by this observation, Mentor (1994a, 1994b, 1997) has developed combined models, which is a clever way of blending the two models together for
computing boundary layer type flows. In this book, only the к – є model is discussed and only to a limited extent.
The к – є turbulence model has been widely used in association with the RANS equations for turbulent mean flow calculations. However, it has been recognized that the applicability of the original к – є model is quite limited. This is because the model contains only a bare minimum of turbulence physics. Also, it is because the unknown constants of the original model were calibrated primarily by using low Mach number boundary layer and two-dimensional mixing layer flow data [see Hanjalic and Launder (1972), Launder and Spalding (1974), Launder and Reece (1975) and Hanjalic and Launder (1976)].
The useful range of the к – є model has since been extended. The extensions were carried out in two ways. First, a number of correction terms, intended to incorporate additional turbulence physics in the model, were proposed. Notable model corrections are the Pope (1978) correction developed for use in three-dimensional jets, the Sarkar and Lakshmanan (1991) correction developed for use when the convective Mach number is not too small, and the Tam and Ganesan (2003) correction developed for nonuniform high-temperature flows. Second, for application to a specific class of turbulent flows, the empirical constants of the original model were recalibrated using a large set of more appropriate data. The motivation for recalibration is the recognition that these constants are not really universal. The model would have a much better chance to be successful if it were applied to a restricted class of flows with similar turbulent mixing characteristics. For each class of flows, a new but more suitable set of constants is used. For instance, for calculating jet and free shear layer mean flows, Thies and Tam (1996) recalibrated the unknown model constants by using a large set of jet flow data covering a wide range of Mach numbers. Their computed jet mean flow velocity profiles for ambient temperature jets were found to be in excellent agreement with experimental measurements. More recently, applications of the recalibrated model to jets in simulated forward flight, coaxial jets, and jets with inverted velocity profile (see Tam, Pastouchenko, and Auriault (2001)) have been carried out with equal success.
The RANS equations including the к – є model in dimensionless form may be written as follows. Here, for jet flows, dimensionless variables with D, Uj, pj, Tj (nozzle exit diameter, jet velocity, density, and temperature) as the length, velocity, density, and temperature scales will be used. Time, pressure, and the turbulence quantities к and є will be nondimensionalized by D/Uj, PjU2j, u2, and uj/D, respectively. Turbulent stresses ті;. and eddy viscosity uT will be nondimensionalized by u2 and Uj /D. In Cartesian tensor notation, the Favre-averaged equations of motion including the к – є model, as well as the Pope, Sarkar, and Tam and Ganesan correction terms (in dimensionless form) are as follows:
Continuity
Momentum
 dp – d(p Тц)
dp – d(p Тц)
dxi dxe
where y is the ratio of specific heats, Pr is the Prandtl number, and Mj is the jet Mach number. There are nine empirical constants in the preceding system. The values recommended by Thies and Tam (1996) and Tam and Ganesan (2004) for jet and similar type of flows are as follows:
C, = 0.0874, Ce1 = 1.40, Ce2 = 2.02, Ce3 = 0.822, Cp = 0.035,
YoT = Pr = 0.422, ok = 0.324, ae = 0.377, a = 0.518
The RANS equations and the к – e model were originally developed with the intention for computing the mean velocity profiles of turbulent flows. The question arises as to whether they can be used for computing unsteady flow and noise. For unsteady flow application, the set of equations is, generally, referred to as Unsteady Reynolds Averaged Navier-Stokes (URANS). Clearly, there are limitations to such
usage. However, the system of URANS equations is relatively simple to use. It requires computational resources that are not too demanding. At present, there is no consensus as to whether it is appropriate to use such a formulation for noise prediction. Evidently, for certain types of problems, its use can be justified, whereas for other types it is not. One must decide based largely on the physics of the problem.












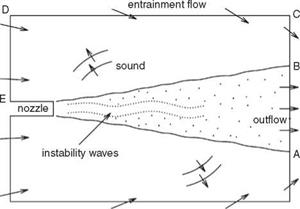 as well as the feedback acoustic waves are much longer than that of the fine-scale turbulence in the mixing layer of the jet. Because of this disparity in length scales, no attempt is made here to resolve the fine-scale turbulence computationally. Based on these considerations, an unsteady RANS model is regarded as adequate. To provide the necessary jet spreading induced by turbulence, the к – e turbulence model is adopted. Here, the к — є model simulates the effect of the fine-scale turbulence on the jet mean flow. In the computation described below, the modified к – e model of Thies and Tam (1996), optimized for jet flows, is used.
as well as the feedback acoustic waves are much longer than that of the fine-scale turbulence in the mixing layer of the jet. Because of this disparity in length scales, no attempt is made here to resolve the fine-scale turbulence computationally. Based on these considerations, an unsteady RANS model is regarded as adequate. To provide the necessary jet spreading induced by turbulence, the к – e turbulence model is adopted. Here, the к — є model simulates the effect of the fine-scale turbulence on the jet mean flow. In the computation described below, the modified к – e model of Thies and Tam (1996), optimized for jet flows, is used.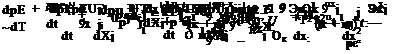
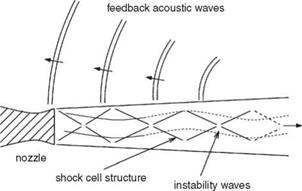 external excitation, acoustic disturbances impinging on this area excite the instability waves. The excited instability waves, extracting energy from the mean flow, grow rapidly as they propagate downstream. After propagating a distance of four to five shock cells, the instability wave, having acquired a large enough amplitude, interacts with the quasiperiodic shock cells in the jet plume. The unsteady interaction generates acoustic radiation, part of which propagates upstream outside the jet. Upon reaching the nozzle lip region, they excite the mixing layer of the jet. This leads to the generation of new instability waves. In this way, the feedback loop is closed.
external excitation, acoustic disturbances impinging on this area excite the instability waves. The excited instability waves, extracting energy from the mean flow, grow rapidly as they propagate downstream. After propagating a distance of four to five shock cells, the instability wave, having acquired a large enough amplitude, interacts with the quasiperiodic shock cells in the jet plume. The unsteady interaction generates acoustic radiation, part of which propagates upstream outside the jet. Upon reaching the nozzle lip region, they excite the mixing layer of the jet. This leads to the generation of new instability waves. In this way, the feedback loop is closed.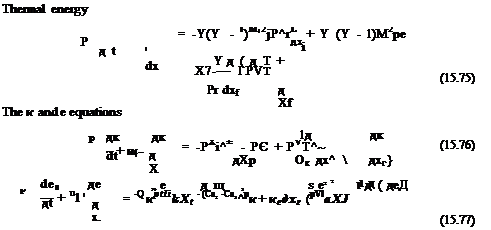
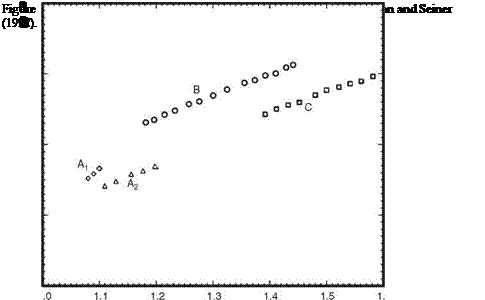
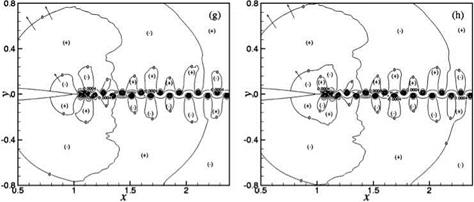
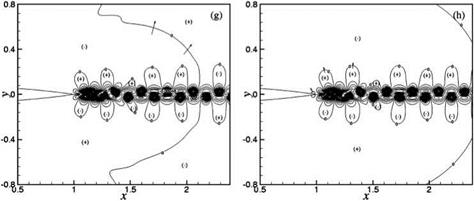
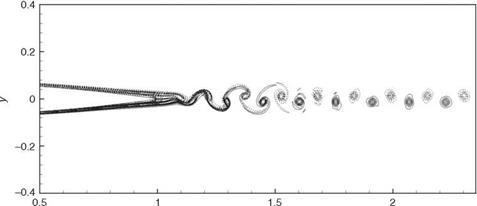
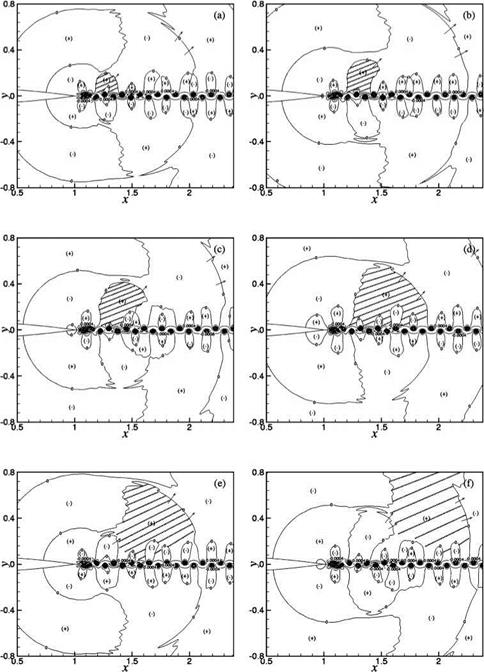
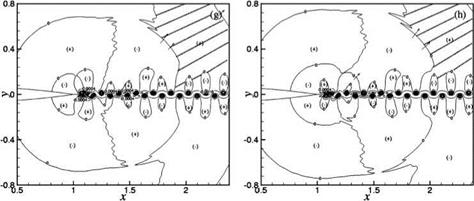
 A study of the space-time data reveals that the tone generation processes are rather complex. There is a dominant mechanism involving the interaction between the near-wake oscillations driven by wake instability and the airfoil trailing edge. However, there are also secondary mechanisms arising from flow and vortex adjustments in the near wake. Details of these tone generation processes can be understood by following the evolution of the wave front contour p = 0 in time. Figure 15.45 illustrates the dominant tone generation process in space and time. Airfoil #2 (2 percent truncation) at Re = 4 x 105 is used in this simulation. Figure 15.45a may be regarded as the beginning of a tone generation cycle. The trailing edge of the airfoil is shown on the left center of the figure. The flow is from left to right. Thus, the wake, defined by two p’ = 0 contours, lies to the right of the airfoil. The near wake is highly unstable. The instability causes the wake to oscillate as can easily be seen in this figure. The wake is flanked by two rows of vortices in a staggered pattern. The spinning motion of the vortices creates a low-pressure region inside the vortices. Hence, all the vortices are located in the p < 0 regions. These regions are labeled by a (-) symbol. Regions with p > 0 are labeled by a (+) symbol. Shown in Figure 15.45a are wave front contours of p = 0. The near-wake instability is antisymmetric with respect to the x-axis. This leads to an antisymmetric pressure field as shown in Figures 15.45a-15.45h. The pressure field shown in Figure 15.45a corresponds to the beginning of the downward motion of the wake in the region just downstream of the airfoil trailing edge. Since the airfoil is stationary, the downward movement of the near wake leads to the creation of a high-pressure region on the top side of the airfoil trailing edge and a corresponding low-pressure region on the mirror image bottom side. This is shown as two small circular regions right at the trailing edge of the airfoil in Figure 15.45b. A small arrow is inserted there to indicate the direction
A study of the space-time data reveals that the tone generation processes are rather complex. There is a dominant mechanism involving the interaction between the near-wake oscillations driven by wake instability and the airfoil trailing edge. However, there are also secondary mechanisms arising from flow and vortex adjustments in the near wake. Details of these tone generation processes can be understood by following the evolution of the wave front contour p = 0 in time. Figure 15.45 illustrates the dominant tone generation process in space and time. Airfoil #2 (2 percent truncation) at Re = 4 x 105 is used in this simulation. Figure 15.45a may be regarded as the beginning of a tone generation cycle. The trailing edge of the airfoil is shown on the left center of the figure. The flow is from left to right. Thus, the wake, defined by two p’ = 0 contours, lies to the right of the airfoil. The near wake is highly unstable. The instability causes the wake to oscillate as can easily be seen in this figure. The wake is flanked by two rows of vortices in a staggered pattern. The spinning motion of the vortices creates a low-pressure region inside the vortices. Hence, all the vortices are located in the p < 0 regions. These regions are labeled by a (-) symbol. Regions with p > 0 are labeled by a (+) symbol. Shown in Figure 15.45a are wave front contours of p = 0. The near-wake instability is antisymmetric with respect to the x-axis. This leads to an antisymmetric pressure field as shown in Figures 15.45a-15.45h. The pressure field shown in Figure 15.45a corresponds to the beginning of the downward motion of the wake in the region just downstream of the airfoil trailing edge. Since the airfoil is stationary, the downward movement of the near wake leads to the creation of a high-pressure region on the top side of the airfoil trailing edge and a corresponding low-pressure region on the mirror image bottom side. This is shown as two small circular regions right at the trailing edge of the airfoil in Figure 15.45b. A small arrow is inserted there to indicate the direction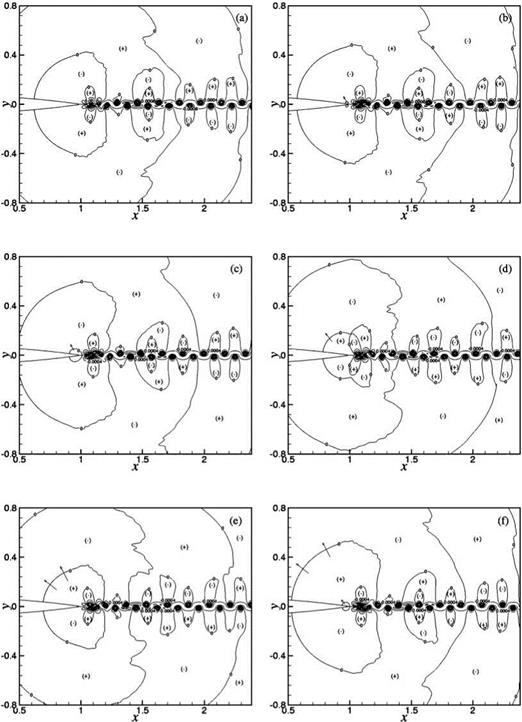

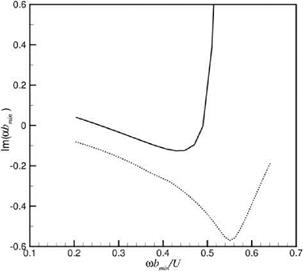 and nonparallel (—– ) instability theo
and nonparallel (—– ) instability theo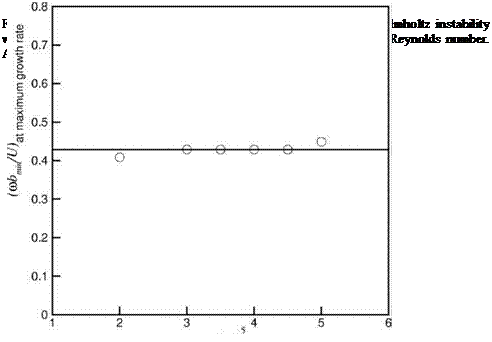
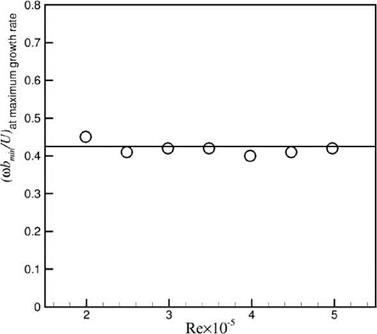
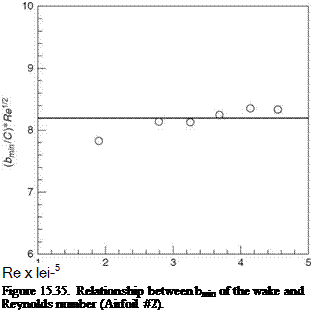
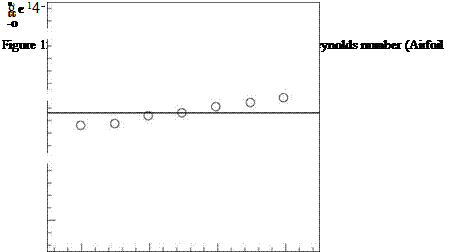



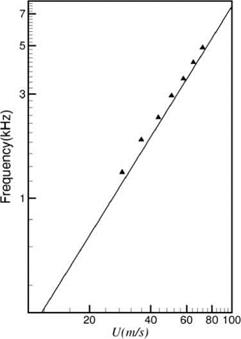
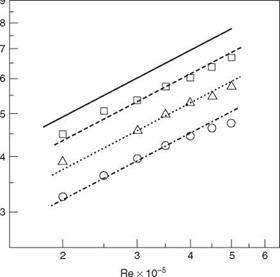 Figure 15.39. Dependence of tone Strouhal number on Reynolds number
Figure 15.39. Dependence of tone Strouhal number on Reynolds number
