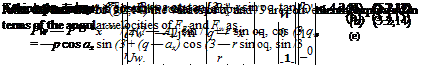FORCE AND MOMENT EQUATIONS IN BODY AXES (EULER’S EQUATIONS)
The force equation of motion in FB is [see (5.4,9)]
fg —
with aqb given by (5.3,16). Again particularizing, as in Sec. 5.5, to the case of a stationary atmosphere, (5.3,18) give the required components of acceleration. With the aerodynamic force in body axes denoted by ~X~
![]()
![]() Y
Y
Z in accordance with traditional usage, and treating gravity as in Sec. 5.5, the scalar equations become
X — mg sin в = т[й + (qEB + q)w — (r®B – j – r)v]
Y + mg cos в sin ф = m[i> + (rEB + r)u — (pEB + p)w] (5.6,2)
Z + mg cos в cos ф — m[w + (pEB + p)v — (qEn + <l)u]
Again, when the Earth rotation can be neglected entirely, (pBB, qEB, fEB) vanish.
The moment equation in frame Fz is (5.4,12), i. e.
G7 = h7 (5.6,3)
or in body axes,
= YBIGZ = hB + Wghg (5.6,4)
The conventional notation for Gg and hв is
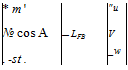
[despite the fact that L is also used for lift (5.5,5)]. In atmospheric flight G normally comes from aerodynamic, propulsive, and control forces; in space flight however, magnetic forces, solar radiation pressure, and gravitational
torques may all contribute importantly to it. The scalar expansion of (5.6,4) is
L = K + qhz — rhy
M = К + rK — phz (5.6,6)
N = К + pK — qh
When mean axes are used, (5.4,28) gives hB, and in that case (5.6,4) can be expressed as
b&b + ^>в-^выв + 2 + 2 &*в^г‘в (5.6,7)
І І
Note that in (5.6,7) the rotation of the Earth does not appear exphcitly, even though no assumption has been made concerning it. It does however occur implicitly in to, which is the angular velocity of FB relative to inertial space. The matrix expansion of (5.6,7) is
(5.6,8)
Owing to its length, there is little advantage in presenting the full scalar expansion of the complete equation (5.6,8). For the restricted case in which S is neghgible, and there are no rotor terms, that is, for a rigid body, it is
L = Ixp- IyZ(q2 – r2) – Izx(r + pq) – Ixy(q – rp) – (Iy – Iz)qr
М = І£ — I Jr2 – p2) – Ixv(p + qr) – Ivz(r – pq) – (Iz – Ix)rp (5.6,9)
N = Izr – Ixy(p2 – q2) – I, Jq + rp) – Izx(p – qr) – (Ix – Iy)pq
It is usually the case for flight vehicles that Gxz is a plane of symmetry.
In that case Ixy = Iyz = 0, and (5.6,9) simplify to
L = IXP — !-Jr + pq) – (Iy – Iz)qr M = Iyq – Izx(r* – p*) – (Iz – Ix)rp (5.6,10)
N = Izr — Izx(p – qr) – (4 – Iy)pq
Finally, when the axes are principal, Izx as well vanishes, and we obtain the simplest form of the moment equations
L = Ixp- (4 – Iz)qr
M = Iyq – (4 – Ix)rp (5.6,11)
N = Izr — (4 – Iv)pq











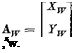 (5.5,4)
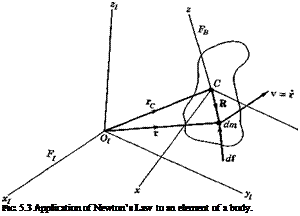
(5.5,4)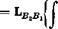 H /gil dm “bj 11 /;, Ato^R^ dm Applying (5.4,17) to the last term, we get
H /gil dm “bj 11 /;, Ato^R^ dm Applying (5.4,17) to the last term, we get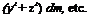

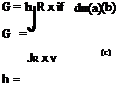

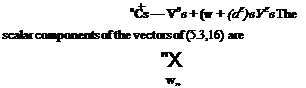

 (5.3,6)
(5.3,6) (5.2,11)
(5.2,11)