Direct Surface Transpiration Concept
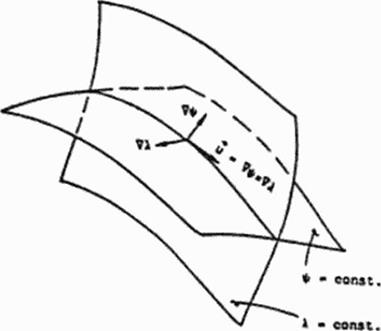
This is an equally simple method of utilizing the transpiration concept which is especially applicable to viscous flow solvers, but the manner of treating boundary conditions on surfaces is different. For example, in the flow analysis w ith Navicr-Stokcs equations, the по-slip condition is imposed at live solid surface by enforcing zero values of all three components of the contravanant velocity vector defined as U = D£/Di. V = D^/Dt. W « D£/Dt. The curv ilinear, non-orthog – onal coordinate system follows the structured computational grid lines. For example, let rj-gnd lines (thus V contravanant clocity component) emanate from the surface of the 3-D object under design consideration. In this inverse shape design concept, the surface pressure distribution, which is obtained from the specified pressure coefficient distribution, is enforced iteratively together with U = W = 0. Tins can he done readily in any existing Navicr-Stokcs flow analysis code 11541- It will result in the contravanant velocity vector component. V. becoming non-zero or ihc surface. Hence, the surface will have to move with iterations or time steps until the convergence is reached, that is. until V « 0 is satisfied on the final surface configuration. This will require that ihc computational grid be regenerated with each update of the surface. Thus. Ihc aerodynamic parameters need to be transfered between old and new grid points by an accurate 3-D interpolation.
|
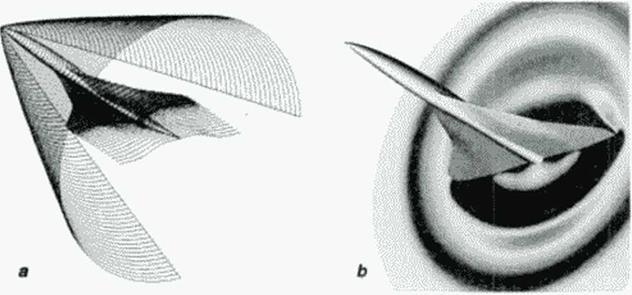
Figure 72 Inverse design of an entire business jet configuration using a high order surface panel code and indirect surface transpiration concept can be performed on a personal computer in less than one hour: a) before, and b) after three optimization cycles enforcing the desired surface pressures. Notice improvements in aerodynamic coefficients {153]. |
This design method will provide for a time-accurate motion of the solid boundaries if the code is executed in a time-accurate mode. For example, it is possible with this method to design a flexible 3-D shape that maintains an essentially steady surface pressure distribution in an otherwise unsteady flow. Specifically, it is possible to determine the correct instantaneous values of local swelling and contraction of a "smart* material coating on the surface thus creating the smart or contmuously-adaptable aerodynamic shape design