If a general two term exponentially growing indicial function is assumed such that
then the Duhamel integral in Eq. 8.74 can be written numerically as
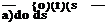 ae(s) = a(s0)(/>(s) + /
ae(s) = a(s0)(/>(s) + /
j So
= a(i0)(l – Ate~b’s – Aie-b*)
/у
+ / — (<7)(1 – – A2e-b^s-a))da
Jso ds
= a(s0) – Аісф0)е b’s ~ A2a(so)e blS + f da(s)
Jso
Notice that the terms Aa(so)e~b’s and A2a(so)e~b2S containing the initial value of a are short-term transients and can be neglected. Therefore, the Duhamel integral can be rewritten
as
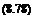 cte{s) = a{s) – X(s) – Y(s),
cte{s) = a{s) – X(s) – Y(s),
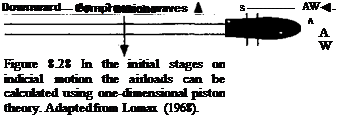
7 Notice that the result in Eq. 8.74 can also be extended to finite wings, where ф represents the indicial aerodynamic response of the entire wing as opposed to a single 2-D section – see Jones (1940) and Lomax (1968).
which is in the notation used by Beddoes (1976, 1984), where the X and Y terms are given by
X(s) = A f o)e-bl{s~a)do, (8.79)
Ло ds
Y(s) = Л2 [ ^(o)e~b2{s-a)do. (8.80)
Ло ds
Assuming a continuously sampled system with time step As (which may be nonuniform) and that so = 0, then we have at the next time step s + As
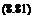 ps+As j
ps+As j
X(s + As) = A / —(o)e~b^s+As~a)do.
Jo ds
Splitting the integral into two parts gives
ps Ary ps~-As Ary
X(s + As) = Axe~b’As / ~—{o)e-bds-^da + A / —(o)e~b'{s+As-a)do Jo ds Js ds
(8.82)
= X(s)e~biAs + Ai / -~(o)e~b'{s+As-a)da
Js ds
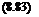 = X(s)e~b’As + /.
= X(s)e~b’As + /.
Notice that this new value, X(s+As), is a one-step recursive formula in terms of the previous value, X(s), and a new increment, /, over the new period. Consider now the evaluation of the I term:
fS + AS J fS+AS J
I = Ax —(a)e-b'(s+As-a)da = Axe-b’is+As) / -~{о)еь’аdo
Js Js
= Aie-b^s+As) / —{o)f{o)do (8.84)
with f(o) = eb’a. At this point, several simplifying assumptions can be made. Introducing a simple backward-difference approximation for da/ds at time 5 + As gives
which has an error of order a"(s 4- As)As. Alternatively, we could use
which has an error of order a"'{s + As)(As)2, although this scheme requires the storage of a at two previous time steps. The remaining part of the integral involving /(cr) can be evaluated exactly and / becomes
 (8.87)
(8.87)
when using Eq. 8.85. Now, if b As is small so that b2(As)2 and higher powers can be neglected, then
Therefore, we obtain the relatively simple result that
It will be seen that this latter result is equivalent to setting f(o) — constant = ebl(-s+As^ over the sample period (i. e., using the rectangle rule of integration) and has a local error of order (As)2. When Eq. 8.89 is introduced into Eq. 8.83, this gives the recurrence formula
X(s + As) = X(s)e~bl As + A, Aas+Aj (8.90)
or
X(s) = X(s – As)e~b, As + A, Aas. (8.91)
Proceeding in a similar fashion for the Y term in Eq. 8.80 gives
ae(s) = a(0) + f da(s) – X(s) – Y(s) = a(s) – X(s) – F(s), (8.92)
Jo
where the X(s) and Y(s) terms are given by the one-step recursive formulas that will be denoted by Algorithm D-l:
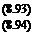 X(s) = X(s – As)e~’biatS + Ai Да, Y(s) = Y(s – As)e~b*As + А2Да,
X(s) = X(s – As)e~’biatS + Ai Да, Y(s) = Y(s – As)e~b*As + А2Да,
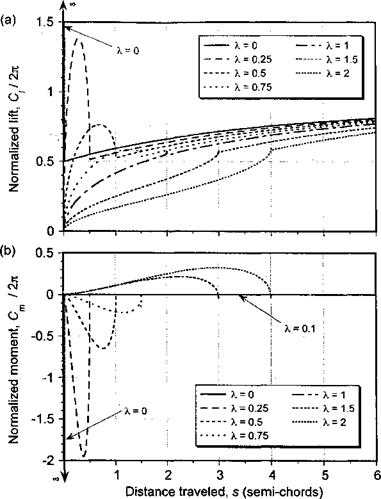
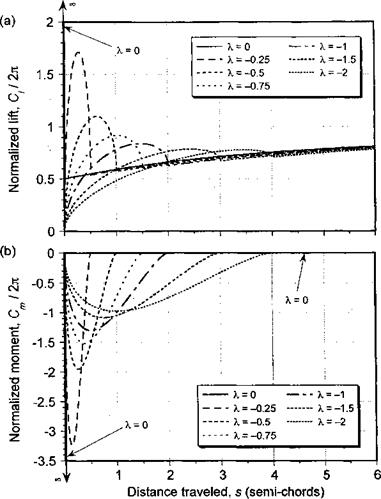
Notice that recursive functions X and Y contain all the time history information of the unsteady aerodynamics and are simply updated once at each time step, thereby providing numerically efficient solutions to the unsteady lift for arbitrary variations in a. Obviously, the above results can be extended to other modes of forcing and to any number of exponential terms that may be used to represent the indicial function. The error in this algorithm results mostly from the approximation used in Eq. 8.88, and it can be shown that the relative error in the integral is
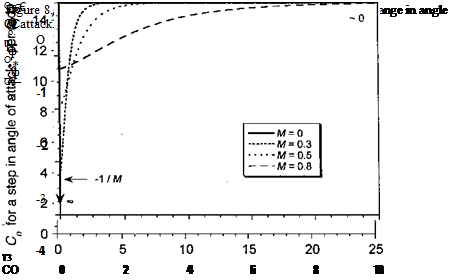
Generally, to obtain errors of less than 5%, each of the products b As and b2As must be less than 0.05. This тр/іііігр. к я rglabvelv «mall time sten and mav not alwavs be oractical in many helicopter rotor problems.
The main reason for adopting an algorithm of this latter form is that there is a significant computational overhead associated with the repetitive numerical evaluation of the formula for I containing the exponential function in Eq. 8.87 versus using the simpler result that / = A AQff+дг; the relative computational cost is a savings of about one order of magnitude (see Fig. 8.27) over using the exact solution. Bearing in mind these algorithms are intended for use in various helicopter rotor analyses where the recurrence formulas may be evaluated tens or hundreds of thousands of times, an order of magnitude extra overhead just to get an exact solution is certainly significant. However, this is at the expense of notable errors
Algorithm number
for practical values of the sampling time step, and the motivation for developing alternative algorithms that are still numerically efficient but have lower numerical errors becomes clear.
If As (or the products bAs or b2As) is large, another approximation based on the midpoint rule can be used. In this case let f(a) « f(s + As/2), and thus
/ = л, е-^+45> fWo
— Axe~bx{s+As) ( A(Xs+As ^ ebx{s+As/2) As As )
= AlAas+Ase~bxAs/2. (8.96)
This gives a method that will be denoted as Algorithm D-2:
ВД = X(s – Дs)e~bxAs + Ai До* e~bxAs/2, (8.97)
Y(s) = Y(s – As)e~blAs + A2Aas e~blAsl2. (8.98)
This recurrence algorithm was first used by Beddoes (1984). This method has a local error of order (As)3, and the relative error in the integral can be shown to be
In this case, Eq. 8.99 suggests that errors of less than 1% from an exact solution will be obtained if both b As and b2As are less than 0.25, which is a much more practically realizable option in a helicopter rotor analysis, despite a notable increase in computational cost. It is, however, still less expensive than the exact solution. See Question 8.8 for a solution to this numerical problem using the trapezoidal rule (Algorithm D-3).











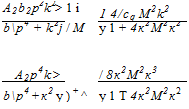
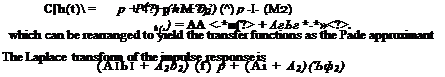
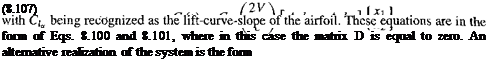
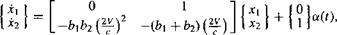 (8.108)
(8.108)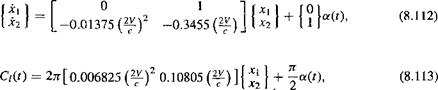
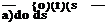 ae(s) = a(s0)(/>(s) + /
ae(s) = a(s0)(/>(s) + /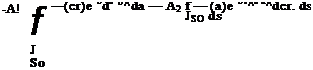
 (8.87)
(8.87)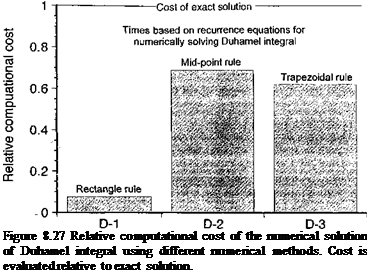
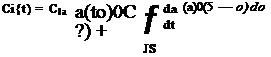

 X = long
X = long