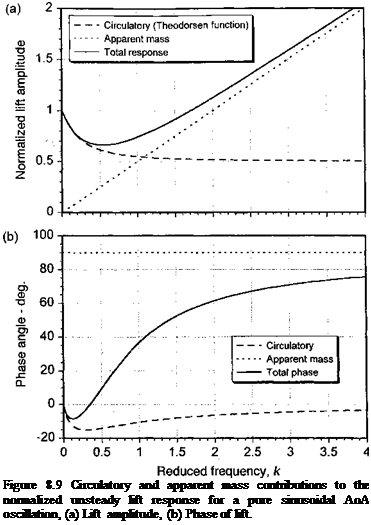
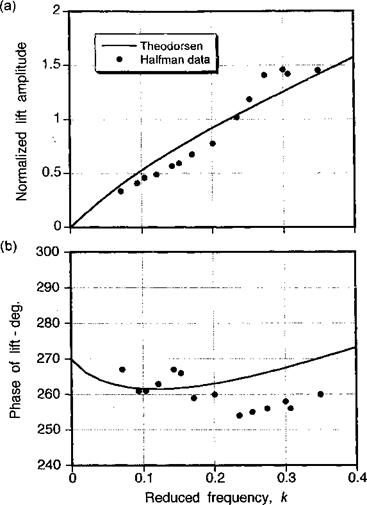
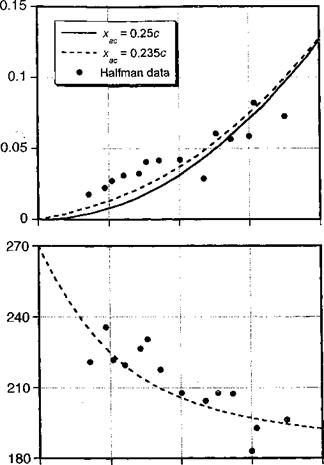
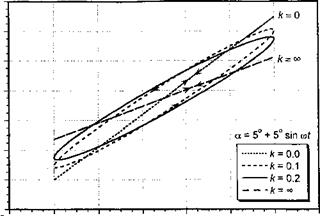
Traveling Sharp-Edged Gust: Miles’s Problem
Results for the lift on a thin 2-D airfoil encountering traveling (in-plane convecting) vertical sharp-edged gusts in incompressible flow have been obtained by Miles (1956) in terms of a gust speed ratio, A:
![]() V
V
x =————- ,
(V +V,)’
where V is the velocity of the airfoil and Vg is the component of the gust convection velocity in the chord plane of the airfoil. The usual assumption made in most rotor aerodynamic analyses is that the wake (tip vortices and corresponding induced velocity field) are stationary (nonconvecting) with respect to the rotor (i. e., rigid wake assumption), so that X — 1 at all the blade elements over the rotor disk. However, the self-induced velocities generated by the vortex wake system results in a continuously changing and nonuniform convection of the induced velocity field with respect to the rotor, and this may produce values of X less than or greater than unity.
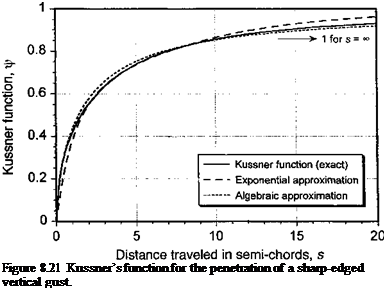
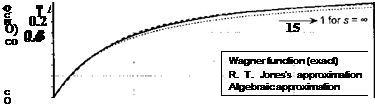
Miles (1956) showed that as the propagation speed of the traveling gust front, Vg, increased from zero to oo (A decreases from 1 to 0), the solution for the unsteady lift changes from the Kiissner result to the Wagner result, with a variety of intermediate transitional results being obtained. Miles’s results were later generalized by Drischler & Diederich (1957) who obtained continuous semi-analytical forms for both the lift and pitching moment gust functions. The problem has also been solved by Leishman (1997) using the reverse flow theorems. All approaches make use of either algebraic or exponential approximations to the Wagner function to facilitate numerical solutions.
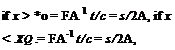 |
|||
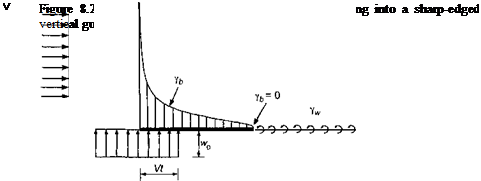
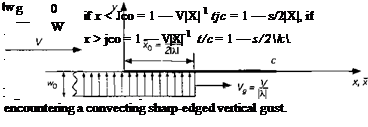
Consider a 2-D airfoil traveling with velocity V and subject to a vertical sharp-edged gust field of magnitude wo convecting with velocity Vg = (A-1 — 1) V, as shown in Fig. 8.22. Notice that when the gust field is stationary, A = 1, and when the field is traveling toward the airfoil at infinite speed, A = 0. For the sharp-edged gust, the primary boundary condition is that the downwash, w, is zero on the part of the airfoil that has not reached the gust front. This means that for a downstream traveling gust referenced to the leading edge then
V
 |
|
and for an upstream traveling gust then
The gust problem is shown schematically in Fig. 8.22. In either case, it will be seen that, like the Kussner problem, the quasi-steady AoA on the airfoil changes progressively as a function of time as the airfoil penetrates into the gust front. For a stationary gust X = 1, and under incompressible flow assumptions, this is equivalent to solving Kussner’s problem. For X == 0, this is equivalent to solving Wagner’s problem.
One approach to solving the convecting gust problem involves using the reciprocal or reverse flow theorems – see Flax (1952, 1953), Brown (1949), Jones (1951), Heaslet & Spreiter (1952), and Leishman (1997). The main utility of reverse flow theorems is that they build from known solutions for airfoil flows and obviate the need to start each new problem from first principles. They are ideally suited to solving various indicial problems, both analytically and numerically. For example, the reverse flow theorems have been used by Leishman (1994) and Hariharan & Leishman (1996) to calculate the indicial responses of airfoils with flaps. General forms of the aerodynamic reverse flow theorems have been established by Heaslet & Spreiter (1952). The first theorem states that: “The lift in steady or indicial motion of one airfoil having arbitrary twist and camber is equal to the integral over the planform of the product of the local AoA and the loading per unit AoA at the corresponding points on a second flat-plate airfoil of identical planform but moving in the reverse direction.” In application, consider two airfoils, one moving in a forward direction and the other in a reverse direction. The first airfoil (the unknown problem) has an arbitrary AoA distribution ai(jci), which could be produced by a vertical gust field (or a flap). The second airfoil is a flat plate at constant angle of attack, аг — constant, which is assumed to have a known aerodynamic loading over the chord. The boundary conditions are «і = a(xi), аг = const. The first reverse flow theorem gives the result that
![]()
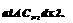
![]()
![]() аг&С Pxdx =
аг&С Pxdx =
In other words, the lift coefficient on the first airfoil can be found from the loading on the second airfoil by integrating the known solution and the local chordwise AoA using
![]() (8.63)
(8.63)
This relatively simple but powerful technique allows some remarkable simplifications in solving both steady and transient airfoil problems. The utility of the theorems, however, extends only to the integrated forces and pitching moments on the airfoil and not to pressure distributions, which may be required for some problems.
For M = 0, the chordwise pressure loading for an indicial change in AoA is given by Eq. 8.46. By using the reverse flow theorems, the time-varying (indicial) lift on the airfoil for a traveling sharp-edged vertical gust can be obtained by integration of this known solution over the appropriate part of the airfoil affected by the gust front, but when the airfoil is moving in the reverse direction. For the downstream traveling vertical gust, this is equivalent to integrating the known flat-plate loading from the trailing edge to the leading edge of the gust front at Jc0 (see Fig. 8.22). For the upstream traveling gust, the known loading must be integrated from the leading edge of the airfoil up to xo. It will be immediately apparent that different results, both quasi-steady and unsteady, will be produced for downstream versus upstream traveling vertical gusts.
For incompressible flows, the noncirculatory part of the unsteady lift can be written in terms of the instantaneous up wash over the airfoil. For a traveling sharp-edged vertical gust, results can be obtained analytically by integrating the first term of Eq. 8.46 with the boundary conditions given in Eqs. 8.60 and 8.61. For a downstream traveling gust the noncirculatory lift can be shown to be
![]() (8.64)
(8.64)
where во = cos_1(l — 2jco), so that 9q = 0 at the time when the gust front is at the airfoil leading edge and во = ж at the trailing edge. For the upstream traveling sharp-edged vertical gust, the corresponding result for the noncirculatory lift is
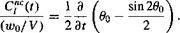 (8.65)
(8.65)
front proceeds over the airfoil, with the time derivatives being evaluated by means of finite differences.
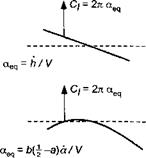
Unlike the apparent mass terms, the circulatory parts of the unsteady lift depend on the prior time history of the gust field, and so the lift must be obtained numerically by Duhamel superposition (see Section 8.14.1 for details). For a downstream traveling gust, the quasi-steady part of the circulatory lift can be obtained analytically by integration of the second term in Eq. 8.46 with the application of the appropriate boundary conditions. For the downstream traveling sharp-edged gust, it can be shown (see Question 8.12) that
the quasi-steady circulatory lift is
![]() Cqs
Cqs
-—L— = 2(тг – в0 – sin6>0) (w0/V)
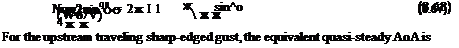
or, in terms of equivalent angle of attack,
The net unsteady circulatory lift is then determined numerically by Duhamel superposition with the instantaneous or quasi-steady equivalent AoA and the Wagner function using Eq. 8.50. The calculation of the corresponding unsteady pitching moments proceeds by a similar process. This problem, however, is somewhat more difficult to solve because a second reverse flow theorem and the chordwise loading as a result of pitch rate must be used in addition to the AoA result – see Leishman (1997).
Results for the unsteady lift and pitching moment for downstream traveling sharp-edged gusts are shown in Fig. 8.23. For A = 0 (Vg = ±oo), the results lead to the Wagner function. For A = 1 (Vg = 0), the results reduce to the Kiissner function. For intermediate values of A, notice that a different series of results are obtained as the gust propagation speed increases from zero (A = 1). The noncirculatory term is responsible for the very large peaks in the lift that are produced as A decreases. The lift reaches a maximum at the point when the airfoil is about naif way into the gust. It can be seen that the magnitudes of these peaks are often larger than the steady-state lift coefficient of 2ж per radian angle of attack. For vertical gusts that move with the wing at velocities less than 0 (A > 1), the noncirculatory part of the lift is small and the circulatory lift grows only very slowly with time. The corresponding pitching moment shows a change in the sign of the center of pressure for A greater or less than one. For the stationary gust (A = 1), the center of pressure remains at the 1/4-chord throughout the motion, a result proved analytically by von Karman & Sears (1938). As the gust speed approaches infinity, the peak in the pitching moment approaches —7T<$(f) with the center of pressure moving to mid-chord. For receding vertical gusts, the center of pressure moves in front of the 1 /4-chord.
Results for upstream traveling vertical gusts are shown in Fig. 8.24. Again, for quickly traveling gusts the results approach the Wagner function. For progressively slower gusts, large peaks in the lift and pitching moment appear as a result of the noncirculatory contributions to the airfoil loading. Notice that the noncirculatory terms are the same for any value of |A| but that the total transient value of the lift is higher than for a downstream traveling gust. The reasons for this will be apparent from a comparison of Eqs. 8.67 and 8.68, which simply prove that a gust affecting the trailing edge of the airfoil will have a larger effect on the circulatory lift than a gust affecting the same percentage of the leading edge. For the same reasons, a trailing edge flap deflection is more effective in producing a change in lift than a leading edge flap.











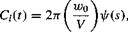 (8.55)
(8.55)