With the increasing number of variables that need to be optimized, the discrete function space containing the optimization variables tends towards a continuous function space for which it is possible to use a global analytical formulation tan adjoint system) instead of the local discretized formulation (gradient search and genetic evolution algorithms). The control theory (adjoint operator) concept is essentially a gradient search optimization approach where the gradient information is obtained by formulating and solving a set of adjoint partial differential equations rather than evaluating the derivatives using finite differencing Like the classical optimization algorithms, the control theory (adjoint operator) formulation can be used either for optimizing a 3-D aerodynamic shape by maximizing its lift, minimizing drag. etc., or it can be used as a tool to enforce the desired surface pressure distribution in an inverse shape design process. If the governing system of partial differential equations is large and the solution space is relatively smooth, then the control theory (adjoint operator) approach is more appropriate than the classical optimization approaches (216J-|2I8). The mathematical formulation is very involved and was only briefly sketched in the previous lecture.
There have been several approaches at creating an aerodynamics control theory (adjoint operator) formulation [216)-I233|. The early efforts (2I6]-[220| were highly mathematical. hard to understand and computationally intensive. Since then, two similar approaches have been followed by most researchers. They are associated with the research teams of Professor A. Jameson (22lJ-[225) who adopted and extended the previous effons by the French researchers, and the research team of Professor V. Modi I226j-(228j who followed a more comprehensible mechanistic approach practised by researchers in the general fields of inverse shape design in elasticity and heal conduction.
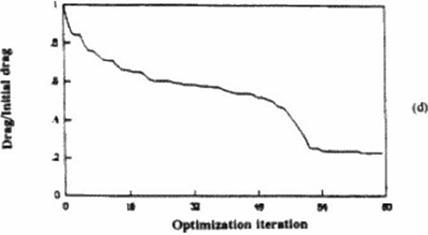
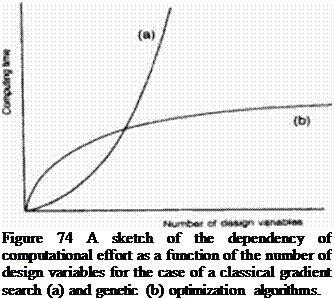
To date, successful and impressive results have been obtained by both research groups where Jameson’s group focused on transonic mviscid flow model and Modi’s group focused on incompressible viscous laminar and turbulent flow models of the flow field Published results of 3-D elbow diffuser and airfoil shape optimization using the adjoint operator approach and incompressible laminar and turbulent flow Navicr-Stokes equations (226)-|228) suggest that a typical optimized design consumes the amount of computing time that is equivalent to between 20 • 40 flow-held analysis (Figure 81. Figure 82). Similar total effort (an equivalent of 30 * 60 flow-field analysis) was reported for 3-D transonic isolated wing design using Euler equations |2I. 22). Tills could be compared with several hundreds and even thousands of flow analysis runs when using a typical genetic algorithm or a typical gradient search optimization algorithm. These results dispel earlier reservations (30) that adjoint operator approach formulations might not be computationally cflicicnt since they involve the solution of the governing flow-field equations. an additional set of adjoint equations, and several more interface partial differential equations.

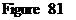 History of the iterative evolution of a minimum drag airfoil starting from a NACA0018 airfoil at Re = 5000. Labeling numbers correspond to the iterative cycles each consisting of one flow-field analysis and one solution of the adjoint system [228].
History of the iterative evolution of a minimum drag airfoil starting from a NACA0018 airfoil at Re = 5000. Labeling numbers correspond to the iterative cycles each consisting of one flow-field analysis and one solution of the adjoint system [228].
Although very impressive and mathematically involved, the general control theory (adjoint operator) approach has certain problems. One drawback is that it does not always allow for flow separation. The method also suffers from tendency to converge to any of the numerous local minima like most of the gradient search optimizers. An additional drawback is that it requires the derivation of an entirely new system of partial differential equations in terms of some non-physical adjoint variables and specification of their boundary conditions. Choosing correct boundary conditions for the adjoint system is quite a challenge since the adjoint variables are not physical flow quantities 1228]. There arc many ways to derive the adjoint system and some additional partial differential equations coupling the onginal system and the adjoint system (221)-[226). If the adjoint system of partial differential equations is different from the original system of the flow-field governing equations, a significant effort needs to be invested in separately coding the two systems. If the adjoint system is almost the same as the original governing system, the numerical algorithms for the two systems arc practically the same and the entire approach could be implemented more readily using the existing CFD analysis software (228J. Actually, if the adjoint system has the same form as the flow-field governing system except that the sign of the convective term in the adjoint system is negative, the solution of the adjoint system will represent a flow in the reverse direction (Figure 83 and Figure 84).
The complexity of the enure adjoint operator formulation makes it difficult to comprehend. implement and modify. Moreover, the adjoint operator formulation is very specific and different formulation needs to be developed and coded for each flow field model (Euler, parabolized Navier-Stokcs. Navier-Stokes. etc.) The control theory (adjoint operator) approach is very attractive if the designers want to use only one specific flow-ticld analysis axle as the basis for a design code and if they want to perform design in only one discipline (for example, aerodynamic shape design only). Since the designers use a variety of progressively more sophisticated design codes during the design process and since the design objectives are inherently multidisciplinary, the control theory (adjoint operator) approach can hardly be justified in the context of the multidisciplinary objectives, funds typically available, and the time limits imposed on the designer
In die case of a truly multidisciplinary problem, a new adjoint sy stem would have to be derived and coded to solve several adjoint systems simultaneously. Since each disciplinary analysis and adjoint system usually has vastly different time scales, the combined multidisciplinary analysis and adjoint system would have a slow convergence rale and an overall marginal stability because of a very large number of local minimums. Reliability of such a design system might be questionable since it is known that sensitivity derivatives for highly non-linear systems might be discontinuous [207J The adjoint system must be discretized for an apptoximation to the gradient to be found. This approach is less reliable than the implicit function theorem approach (231), (2321. Therefore, finding the gradients of the objective function using information from the discretized flow-field governing equations is more reliable (2321 than if an analytic expression for the gradient is derived in terms of the exact flow-field solution and the solution to the adjoint sy stem [223].
|

Figure 83 Horizontal components of the fluid velocity vector at different axial locations; the flow is from left to right [228].
|
|
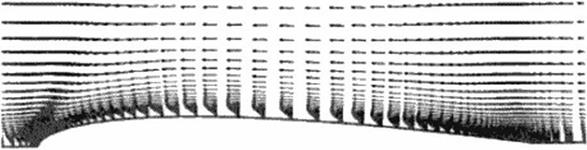
Figure 84 Horizontal components of an adjoint variable at different axial locations; the "flow" of the adjoint vector is in the opposite direction to the physical fluid flow if the adjoint system is made to resemble the flow-fleld governing system except for the change in sign of the convective term [228].
|
An attractive extension of the control theory (adjoint <*perator) approach represents the "one-shot" method [234M237J. It implicitly combines a multigrid solution technique with the classical control theory for systems of partial differential equations. Consequently, this approach is faster than the regular control theory (adjoint operator) approach where the multi – grid technique was used only to accelerate the flow-field analysis code 1225). Nevertheless, the "one-shot”’ formulation and implementation are even more complex than the control theory (adjoint operator) formulation, and it suffers from similar reliability issues due to the fact that it might be equally prone to the local minima
12.3 Conclusions
A number of existing and emerging concepts and methodologies applicable to automatic inverse design and optimization of arbitrary realistic 3-D configurations have recently been surveyed and compared [2351. These attempt* to classify the design methods and to expose their major advantages and disadvantages resulted in the following conclusions:
• control theory (adjoint operator) algorithms offer very economical shape design optimization although they arc complex to understand and develop, hard to modify, too field-specific. and prone to local minima.
• one-shot method should be further researched as an esen more economical possible successor to the adjoint operator formulations w ith all of its drawbacks, and
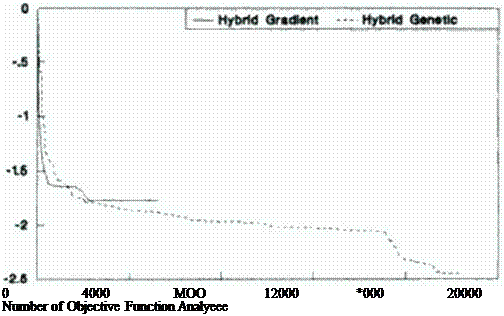
• combination of hybrid genetic/gradient search constrained optimization of surface pressure distribution followed by transpiration inverse design offers an attractive approach in the immediate future because of its unsurpassed robustness and acceptable computing cost.












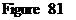 History of the iterative evolution of a minimum drag airfoil starting from a NACA0018 airfoil at Re = 5000. Labeling numbers correspond to the iterative cycles each consisting of one flow-field analysis and one solution of the adjoint system [228].
History of the iterative evolution of a minimum drag airfoil starting from a NACA0018 airfoil at Re = 5000. Labeling numbers correspond to the iterative cycles each consisting of one flow-field analysis and one solution of the adjoint system [228].

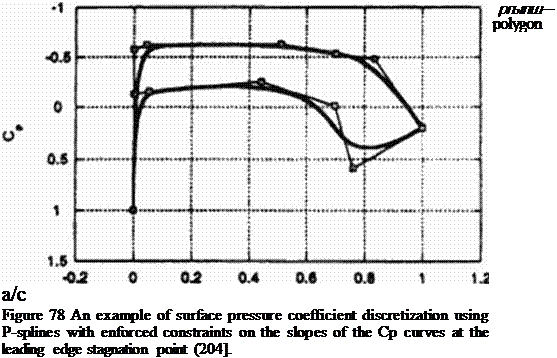


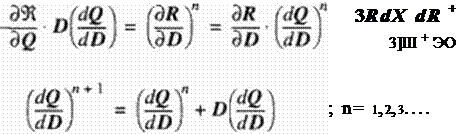
![Подпись: Figure 73 Winglets on a Japanese space plane were successfully redesigned using the integro-differential equation approach and a Navier-Stokes flow-field analysis code [161].](/img/3131/image154_3.gif)