Category THEORETICAL AERODYNAMICS

In the preceding sections of this chapter, the discussions were for incompressible flows, where the density can be regarded as constant. But in many engineering applications, such as designing buildings to withstand winds, the design of engines and of vehicles of all kinds – cars, yachts, trains, aeroplane, missiles and launch vehicles require a study of the flow with velocities at which the gas cannot be treated as incompressible. Indeed, the flow becomes compressible. Study of such flows where the changes in both density and temperature associated with pressure change become appreciable is called gas dynamics. In other words, gas dynamics is the science of fluid flows where the density and temperature changes become important. The essence of the subject of gas dynamics is that the entire flow field is dominated
by Mach waves, expansion waves and shock waves, when the flow speed is supersonic. It is through these waves that the change of flow properties from one state to another takes place. In the theory of gas dynamics, change of state in flow properties is achieved by three means: (a) with area change, treating the fluid to be inviscid and passage to be frictionless, (b) with friction, treating the heat transfer between the surrounding and system to be negligible and (c) with heat transfer, assuming the fluid to be inviscid. These three types of flows are called isentropic flow, frictional or Fanno type flow and Rayleigh type flow, respectively.

All problems in gas dynamics can be classified under the three flow processes described above, of course with the assumptions mentioned. Although it is impossible to have a flow process which is purely isentropic or Fanno type or Rayleigh type, in practice it is justified in assuming so, since the results obtained with these treatments prove to be accurate enough for most practical problems in gas dynamics. Even though it is possible to solve problems with mathematical equations and working formulae asso­ciated with these processes, it is found to be extremely useful and time saving if the working formulae are available in the form of tables with a Mach number which is the dominant parameter in compressible flow analysis.

Fluid flow through pipes with circular and noncircular cross-sections is one of the commonly encountered problems in many practical systems. Flow through pipes is driven mostly by pressure or gravity or both.

Vi

(a)

Steady laminar flow

/V’ (measured from V)

V

t

(b) Steady turbulent flow Vi /V’ (measured from V)

t

(c) Unsteady turbulent flow

Consider the flow in a long duct, shown in Figure 2.27. This flow is constrained by the duct walls. At the inlet, the freestream flow (assumed to be inviscid) converges and enters the tube.

Because of the viscous friction between the fluid and pipe wall, viscous boundary layer grows down­stream of the entrance. The boundary layer growth makes the effective area of the pipe to decrease progressively downstream, thereby making the flow along the pipe to accelerate. This process continues up to the point where the boundary layer from the wall grows and meets at the pipe centerline, that is, fills the pipe, as illustrated in Figure 2.27.

The zone upstream of the boundary layer merging point is called the entrance or Bow development length Le and the zone downstream of the merging point is termed fully developed region. In the fully developed region, the velocity profile remains unchanged. Dimensional analysis shows that Reynolds number is the only parameter influencing the entrance length. In the functional form, the entrance length can be expressed as:

f (p, V, d, V)

fj pPVd i

where p, V and Vare the flow density, velocity and viscosity, respectively, and d is the pipe diameter. For laminar flow, the accepted correlation is:

At the critical Reynolds number Rec = 2300, for pipe flow, Le = 138d, which is the maximum develop­ment length possible.

For turbulent flow the boundary layer grows faster, and Le is given by the approximate relation:

Now, examine the flow through an inclined pipe, shown in Figure 2.28, considering the control volume between sections 1 and 2.

Treating the flow to be incompressible, by volume conservation, we have:

Q2 = constant

Q = V, = Q Ai 2 A2’

where Qi and Q2, respectively, are the volume flow rates and A1, A2, V1 and V2 are the local areas and velocities, at states 1 and 2. The velocities V1 and V2 are equal, since the flow is fully developed and also Ai = A2.

By incompressible Bernoulli’s equation, we have:

where Az = (z1 — z2) and Ap = (p1 — p2). That is, the head loss (in a pipe), due to friction is equal to the sum of the change in gravity head and pressure head.

By momentum balance, we have:

ApnR2 + pg(nRz) AL sin0 — rw(2nR) AL = m(V1 — V2) = 0.

Dividing throughout by (nR2)pg, we get:

——- + AL sin в

Pg

But AL sin в = Az. Thus:

Ap 2tw AL

—- + Az =————

Pg Pg R

Using Equation (2.72), we obtain:

In the functional form, the wall shear tw may be expressed as:

tw = F(p, V, p, d, e),

where p is viscosity of the fluid, d is the pipe diameter, and e is the wall roughness height. By dimensional analysis, Equation (2.75) may be expressed as:

<2-76)

where f is called the Darcy friction factor, which is a dimensionless parameter.

Combining Equations (2.74) and (2.76), we obtain the pipe head loss as:

This is called the Darcy-Weisbach equation, valid for flow through ducts of any cross-section. Further, in the derivation of the above relation, there was no mention about whether the flow was laminar or turbulent and hence Equation (2.77) is valid for both laminar and turbulent flows. The value of friction factor f for any given pipe (that is, for any surface roughness e and d) at a given Reynolds number can be read from the Moody chart (which is a plot of f as a function of Red and e/d).

It is essential to note that in our discussions here it is mentioned that, decrease of pipe area due to boundary layer, results in increase of flow velocity. This is possible only in subsonic flows. When the flow is supersonic, decrease in area will decelerate the flow [2].

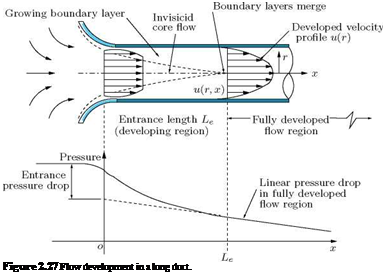
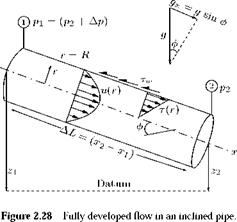
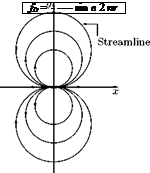
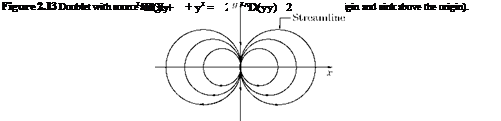
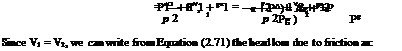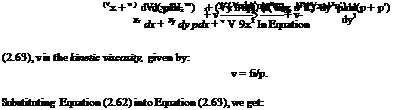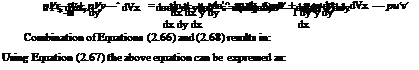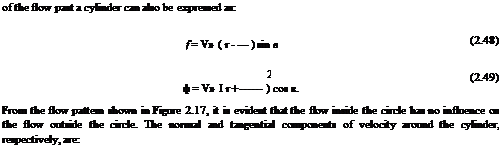In low-speed flow past geometrically similar bodies with identical orientation and relative roughness, the drag coefficient should be a function of the Reynolds number only.

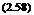Cd = f (Re).

The Reynolds number is based upon freestream velocity V» and a characteristic length L of the body. The drag coefficient Cd could be based upon L2, but it is customary to use a characteristic area S of the body instead of L2. Thus, the drag coefficient becomes:

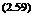c _ Drag D 1PV*. S’

The factor -, in the denominator of the Cd expression, is our traditional tribute to Euler and Bernoulli. The area S is usually one of the following three types:

1. Frontal area of the body as seen from the flow stream. This is suitable for thick stubby bodies, such as spheres, cylinders, cars, missiles, projectiles, and torpedos.

2. Planform area of the body as seen from above. This is suitable for wide flat bodies such as aircraft wings and hydrofoils.

3. Wetted area. This is appropriate for surface ships and barges.

While using drag or other fluid (aerodynamic) force data, it is important to note what length and area are being used to scale the measured coefficients.

Table 2.2 gives a few data on drag, based on frontal area, of two-dimensional bodies of various cross­section, at Re > 104.

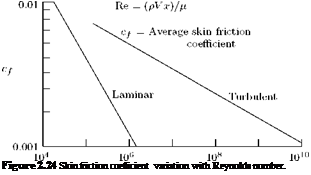
Drag coefficient of sharp-edged bodies, which have a tendency to experience flow separation regardless of the nature of boundary layer, are insensitive to Reynolds number. The elliptic cylinders, being smoothly rounded, have the “laminar-turbulent” transition effect and are therefore quite sensitive to the nature of the boundary layer (that is, laminar or turbulent).

Table 2.3 lists drag coefficients of some three-dimensional bodies. For these bodies also we can conclude that sharp edges always cause flow separation and high drag which is insensitive to Reynolds number.

Rounded bodies, such as ellipsoid, have drag which depends upon the point of separation, so that both Reynolds number and the nature of boundary layer are important. Increase of body length will generally decrease the pressure drag by making the body relatively more slender, but sooner or later the skin friction drag will catch up. For a flat-faced cylinder, the pressure drag decreases with L/d but the skin friction

2.12.1 Turbulence

Turbulent flow is usually described as flow with irregular fluctuations. In nature, most of the flows are turbulent. Turbulent flows have characteristics which are appreciably different from those of laminar flows. We have to explain all the characteristics of turbulent flow to completely describe it. Incorporat­ing all the important characteristics, the turbulence may be described as a three-dimensional, random phenomenon, exhibiting multiplicity of scales, possessing vorticity and showing very high dissipation. Turbulence is described as a three-dimensional phenomenon. This means that even in a one-dimensional flow field the turbulent fluctuations are always three-dimensional. In other words, the mean flow may be one – or two – or three-dimensional, but the turbulence is always three-dimensional. From the above discussions, it is evident that turbulence can only be described and cannot be defined.

A complete theoretical approach to turbulent flow similar to that of laminar flow is impossible because of the complexity and apparently random nature of the velocity fluctuations in a turbulent flow. Nevertheless, semi-theoretical analysis aided by limited experimental data can be carried out for turbulent flows, with instruments which have the capacity to detect high-frequency fluctuations. For flows at very low-speeds, say around 20 m/s, the frequencies encountered will be 2 to 500 Hz. Hot-wire anemometer is well suited for measurements in such flows. A typical hot-wire velocity trace of a turbulent flow is shown in Figure 2.25. Turbulent fluctuations are random, in amplitude, phase and frequency. If an instrument such as a pitot-static tube, which has a low frequency response of the order of 30 seconds, is used for the measurement of velocity, the manometer will read only a steady value, ignoring the fluctuations. This means that the turbulent flow consists of a steady velocity component which is independent of time, over which the fluctuations are superimposed, as shown in Figure 2.25(b). That is:

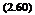U(t) = U + u'(t),

U = U + u'(t)

where U (t) is the instantaneous velocity, U is the time averaged velocity, and u/(t) is the turbulent fluctuation around the mean velocity. Since U is independent of time, the time average of u'(t) should be equal to zero. That is:

t

u'(t) = 0 ; u’ = 0,

provided the time t is sufficiently large. In most of the laboratory flows, averaging over a few seconds is sufficient if the main flow is kept steady.

In the beginning of this section, we saw that the turbulence is always three-dimensional in nature even if the main flow is one-dimensional. For example, in a fully developed pipe or channel flow, as far as the mean velocity is concerned only the x-component of velocity U alone exists, whereas all the three components of turbulent fluctuations u’, v’ and w’ are always present. The intensity of the turbulent velocity fluctuations is expressed in the form of its root mean square value. That is, the velocity fluctuations are instantaneously squared, then averaged over certain period and finally square root is taken. The root mean square (RMS) value is useful in estimating the kinetic energy of fluctuations. The turbulence level for any given flow with a mean velocity U is expressed as a turbulence number n, defined as:

. /12 . /2 . /2

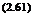
V u + v + w

3U

In the laboratory, turbulence can be generated in many ways. A wire-mesh placed across an air stream produces turbulence. This turbulence is known as grid turbulence. If the incoming air stream as well as the mesh size are uniform then the turbulent fluctuations behind the grid are isotropic in nature, that is, u’, v’, w’ are equal in magnitude. In addition to this, the mean velocity is the same across any cross­section perpendicular to the flow direction, that is, no shear stress exists. As the flow moves downstream the fluctuations die down due to viscous effects. Turbulence is produced in jets and wakes also. The mean velocity in these flows varies and they are known as free shear flows. Fluctuations exist up to some distance and then slowly decay. Another type of turbulent flow often encountered in practice is
the turbulent boundary layer. It is a shear flow with zero velocity at the wall. These flows maintain the turbulence level even at large distance, unlike the grid or free shear flows. In wall shear flows or boundary layer type flows, turbulence is produced periodically to counteract the decay.

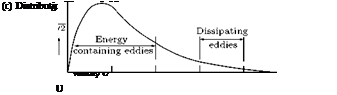
A turbulent flow may be visualized as a flow made up of eddies of various sizes. Large eddies are first formed, taking energy from the mean flow. They then break up into smaller ones in a sequential manner till they become very small. At this stage the kinetic energy gets dissipated into heat due to viscosity. Mathematically it is difficult to define an eddy in a precise manner. It represents, in a way, the frequencies involved in the fluctuations. Large eddy means low-frequency fluctuations and small eddy means high-frequency fluctuations encountered in the flow. The kinetic energy distribution at various frequencies can be represented by an energy spectrum, as shown in Figure 2.25(c).

The problem of turbulence is yet to be solved completely. Different kinds of approach are employed to solve these problems. The well-known method is to write the Navier-Stokes equations for the fluctuating quantities and then average them over a period of time, substituting the following [in Navier-Stokes equations, Equation (2.23)]:

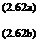Vx = Vx + u, Vy = Vy + v’, Vz = Vz + w’

p = p + p,

where Vx, u’, Vy, v’, Vz, w’ are the mean and fluctuational velocity components along x-, y – and z-directions, respectively, and p, p’, respectively, are the mean and fluctuational components of pressure p. Bar denotes the mean values, that is, time averaged quantities.

Let us now consider the x-momentum equation [Equation (2.23)] for a two-dimensional flow:

Expanding Equation (2.64), we obtain:

In this equation, time average of the individual fluctuations is zero. But the product or square terms of the fluctuating velocity components are not zero. Taking time average of Equation (2.65), we get:

Equation (2.66) is slightly different from the laminar Navier-Stokes equation (Equation 2.63). The continuity equation for the two-dimensional flow under consideration is:

This can be expanded to result in:

The terms involving turbulent fluctuational velocities u’ and v’ on the left-hand side of Equation (2.66) can be written as:

The terms —pul and —pu’v’ in Equation (2.69) are due to turbulence. They are popularly known as Reynolds or turbulent stresses. For a three-dimensional flow, the turbulent stress terms are pul, pv’2, pw’2, pu’v’, pv’w’ and pw’u’. Solutions of Equation (2.69) is rather cumbersome. Assumptions like eddy viscosity, mixing length are made to find a solution for this equation.

At this stage, it is important to have proper clarity about the laminar and turbulent flows. The laminar flow may be described as “ a well orderly pattern where fluid layers are assumed to slide over one another,” that is, in laminar flow the fluid moves in layers, or laminas, one layer gliding over an adjacent layer with interchange of momentum only at molecular level. Any tendencies toward instability and turbulence are damped out by viscous shear forces that resist the relative motion of adjacent fluid layers. In other words:

“laminar flow is an orderly flow in which the fluid elements move in an orderly manner such that the transverse exchange of momentum is insignificant”

and

“turbulent flow is a three-dimensional random phenomenon, exhibiting multiplicity of scales, pos­sessing vorticity and showing very high dissipation. ”

Turbulent flow is basically an irregular flow. Turbulent flow has very erratic motion of fluid particles, with a violent transverse exchange of momentum.

The laminar flow, though possesses irregular molecular motions, is macroscopically a well-ordered flow. But in the case of turbulent flow, there is the effect of a small but macroscopic fluctuating velocity superimposed on a well-ordered flow. A graph of velocity versus time at a given position in a pipe flow would appear as shown in Figure 2.26(a), for laminar flow, and as shown in Figure 2.26(b), for turbulent flow. In Figure 2.26(b) for turbulent flow, an average velocity denoted as V has been indicated. Because this average is constant with time, the flow has been designated as steady. An unsteady turbulent flow may prevail when the average velocity field changes with time, as shown in Figure 2.26(c).

The friction between the surface of a body and the fluid causes viscous shear stress and this force is known as skin friction drag. Wall shear stress т at the surface of a body is given by:

where g is the dynamic viscosity coefficient and dVx/dy is the velocity gradient at body surface y = 0. If the velocity profile in the boundary layer is known, then the shear stress can be calculated.

For streamlined bodies, the separated zone being small, a major portion of the drag is because of skin friction. We saw that bodies are classified as streamlined and bluff, based on which is dominant among the drag components. A body for which the skin friction drag is a major portion of the total drag is termed streamlined body. A body for which the pressure (form) drag is the major portion is termed bluff body. Turbulent boundary layer results in more skin friction than a laminar one. Examine the skin friction coefficient cf variation with Reynolds number, for a flat plate kept at zero angle of attack in a uniform stream, plotted in Figure 2.24. The characteristic length for Reynolds number is the plate length x, from its leading edge. It can be seen from Figure 2.24 that the Cf is more for a turbulent flow than laminar flow. The friction coefficient is defined as:

where V», p are the freestream velocity and density, respectively, and S is the wetted surface area of the flat plate.

For bluff bodies, the pressure drag is substantially greater than the skin friction drag, and for streamlined bodies the condition is the reverse. In the case of streamlined bodies, such as aerofoil, the designer aims at keeping the skin friction drag as low as possible. Maintaining laminar boundary layer conditions all along the surface is the most suitable arrangement to keep the skin friction low. Though such aerofoils, known as laminar aerofoils, have been designed, they have many limitations. Even a small surface roughness or disturbance can make the flow turbulent, and spoil the purpose of maintaining the laminar flow over the entire aerofoil. In addition, for laminar aerofoils there is a tendency for the flow to separate even at small angles of attack, which severely restricts the use of such aerofoils.

The pressure drag arises due to the separation of boundary layer, caused by adverse pressure gradient. The phenomenon of separation, and how it causes the pressure drag, can be explained by considering flow around a body, such as a circular cylinder. If the flow is assumed to be potential, there is no viscosity and hence no boundary layer. The flow past the cylinder would be as shown in Figure 2.22, without any separation.

Potential flow around a cylinder will be symmetrical about both the horizontal and vertical planes, passing through the center of the cylinder. The pressure distribution over the front and back surfaces would be identical, and the net force along the freestream direction would be zero. That is, there would

not be any drag acting on the cylinder. But in real flow, because of viscosity, a boundary layer is formed over the surface of the cylinder. The flow experiences a favorable pressure gradient from the forward stagnation point to the topmost point A on the cylinder at в = 90°, shown in Figure 2.22.

Therefore, the flow accelerates from point to A (that is, from в = 0° to 90°). However, beyond

в = 90° the flow is subjected to an adverse pressure gradient and hence decelerates. Note that beyond the topmost point A the fluid elements find a larger space to relax. Therefore, in accordance with mass conservation (for subsonic flow) [2], as the flow area increases the flow speed decreases and the pressure increases. Under this condition there is a net pressure force acting against the fluid flow. This process establishes an adverse pressure gradient, leading to flow separation, as illustrated in Figure 2.23. In a boundary layer, the velocity near the surface is small, and hence the force due to its momentum is unable to counteract the pressure force. Flow within the boundary layer gets retarded and the velocity near the wall region reduces to zero at some point downstream of A and then the flow is pushed back in the opposite direction, as illustrated in Figure 2.23. This phenomenon is called flow separation.

The location where the flow leaves the body surface is termed separation point. For flow past a cylinder, there are two separation points on either side of the horizontal axis through the center of the cylinder. The separated flow is chaotic and vortex dominated. The separated flow behind an object is also referred to as wake. Depending on the Reynolds number level, the wake may be laminar or turbulent. An important characteristics of the separated flow is that it is always unsymmetrical, even for laminar

separation. This is because of the vortices prevailing in the separated zone. As we know, for every vortex there is a specific frequency and amplitude. Therefore, when the vortices formed at the upper and lower separation points of the cylinder are of the same size and leave the cylinder at the same time, the wake must be symmetric. But this kind of formation of vortices of identical size and leaving the upper and lower separation points at the same time is possible only when the geometry of the cylinder is perfectly symmetrical and the freestream flow is absolutely unperturbed and symmetrical about the horizontal plane bisecting the cylinder. But in practice it is not possible to meet these stringent requirements of flow and geometrical symmetry to establish symmetrical separation. Owing to this practical constraints all separated flows are unsymmetrical. Indeed, the formation of the vortices at the upper and lower separation points itself is unsymmetrical. When one of them, say the upper one, grows faster, the other one is unable to grow at the same rate. Therefore, only after the faster growing vortex reaches a limiting size possible, for the geometry and Reynolds number combination, and leaves the surface, the growth of the vortex at the opposite side picks up. This retards the growth of the new vortex formed at the location where the vortex left the surface. Thus, alternative shedding of vortices from the upper and lower separation points is established. The alternative shedding of vortices makes the wake chaotic.

Across the separated region, the total pressure is nearly a constant and lower than what it would have been if the flow did not separate. The pressure do not recover completely as in the case of potential flow. Thus, on account of the incomplete recovery of pressure due to separation, a net drag force opposing the body motion is generated. We can easily see that the pressure drag will be small if the separation had taken place later, that is, the area over which the pressure unrecovered is small. To minimize pressure drag, the separation point should be as far as possible from the leading edge or forward stagnation point. This is true for any shape. Streamlined bodies are designed on this basis and the adverse pressure gradient is kept as small as possible, by keeping the curvature very small. At this stage, it is important to realize that the separated region behind an object is vortex dominated and these vortices cause considerable pressure loss. Thus the total pressure _P0,rear behind the object is significantly lower than the total pressure _P0,face at the face of the object. This difference (p0,rear — _P0,face), termed pressure loss, is a direct measure of the drag. This drag caused by the pressure loss is called the pressure drag. This is also referred to as form drag, because the form or shape of the moving object dictates the separation and the expanse of the separated zone. The separation zone behind an object is also referred to as wake. That is, wake is the separated region behind an object (usually a bluff body) where the pressure loss is severe. It is essential to note that what is meant by pressure loss is total pressure loss, and there is nothing like static pressure loss.

The separation of boundary layer depends not only on the strength of the adverse pressure gradient but also on the nature of the boundary layer, namely, laminar or turbulent. A laminar flow has tendency to separate earlier than a turbulent flow. This is because the laminar velocity profiles in a boundary layer has lesser momentum near the wall. This is conspicuous in the case of flow over a circular cylinder. Laminar boundary layer separates nearly at в = 90° whereas, for a highly turbulent boundary layer the separation is delayed and the attached flow continues up to as far as в = 150° on the cylinder. The reduction of pressure drag when the boundary layer changes from laminar to turbulent is of the order of 5 times for bluff bodies. The flow behind a separated region is called the wake. For low drag, the wake width should be small.

Although separation is shown to take place at well defined locations on the body, in the illustration in Figure 2.23, it actually takes places over a zone on the surface which can not be identified easily. Therefore, theoretical estimation of separation especially for a turbulent boundary layer is difficult and hence the pressure drag cannot be easily calculated. Some approximate methods exist but they can serve only as guidelines for the estimation of pressure drag.

At this stage, we may wonder about the level of static pressure in the separated flow region or the wake of a body. The total pressure in the wake is found to be lower than that in the freestream, because of the pressure loss caused by the vortices in the wake. But the static pressure in the wake is almost equal to the freestream level. But it is essential to realize that just after separation, the flow is chaotic and the streaklines do not exhibit any defined pattern. Therefore, the static pressure does not show any specific mean value in the near-wake region and keeps fluctuating. However, beyond some distance behind the
object, the wake stabilizes to an extent to assume almost constant static pressure across its width. This distance is about 6 times the diameter for a circular cylinder. Thus, beyond 6 diameter distance the static pressure in the wake is equal to the freestream value.

Note: It may be useful to recall what is meant by pressure loss is the total pressure loss and there is nothing like static pressure loss.

When a body moves in a fluid, it experiences forces and moments due to the relative motion of the flow taking place around it. If the body has an arbitrary shape and orientation, the flow will exert forces and moments about all the three coordinate axes, as shown in Figure 2.21. The force on the body along the flow direction is called drag.

The drag is essentially a force opposing the motion of the body. Viscosity is responsible for a part of the drag force, and the body shape generally determines the overall drag. The drag caused by the viscous effect is termed the frictional drag or skin friction. In the design of transport vehicles, shapes experiencing minimum drag are considered to keep the power consumption at a minimum. Low drag shapes are called streamlined bodies and high drag shapes are termed bluff bodies.

Drag arises due to (a) the difference in pressure between the front and rear regions and (b) the friction between the body surface and the fluid. Drag force caused by the pressure imbalance is known as pressure drag, and (b) the drag due to friction is known as skin friction drag or shear drag. A body for which the skin friction drag is the major portion of the total drag is called streamlined body, and that with the pressure drag as the major portion of the total drag is called a bluff body.

In the previous sections of this chapter, we have seen many interesting concepts of fluid flow. With this background, let us observe some of the important aspects of fluid flow from a practical or application point of view.

We are familiar with the fact that the viscosity produces shear force which tends to retard the fluid motion. It works against inertia force. The ratio of these two forces governs (dictates) many properties of the flow, and the ratio expressed in the form of a nondimensional parameter is known as the famous Reynolds number, ReL:

where V, p are the velocity and density of the flow, respectively, g is the dynamic viscosity coefficient of the fluid and L is a characteristic dimension. The Reynolds number plays a dominant role in fluid flow analysis. This is one of the fundamental dimensionless parameters which must be matched for similarity considerations in most fluid flow analyses. At high Reynolds numbers, the inertia force is predominant compared to viscous forces. At low Reynolds numbers the viscous effects predominate everywhere, whereas at high Re the viscous effects confine to a thin region, just adjacent to the surface of the object present in the flow, and this thin layer is termed boundary layer. Since the length and velocity scales are chosen according to a particular flow, when comparing the flow properties at two different Reynolds numbers, only flows with geometric similarity should be considered. In other words, flow over a circular cylinder should be compared only with flow past another circular cylinder, whose dimensions can be different but not the shape. Flow in pipes with different velocities and diameters and flow over aerofoils of the same kind are also some geometrically similar flows. From the above-mentioned similarity consideration, we can infer that geometric similarity is a prerequisite for dynamic similarity. That is, dynamically similar flows must be geometrically similar, but the converse need not be true. Only similar flows can be compared, that is, when comparing the effect of viscosity, the changes in flow pattern due to body shape should not interfere with the problem.

For calculating Reynolds number, different velocity and length scales are used. Some popular shapes and their length scales we often encounter in fluid flow studies are given in Table 2.1. In the description of Reynolds number here, the quantities with subscript to are at the freestream and quantities without subscript are the local properties. Reynolds number is basically a similarity parameter. It is used to determine the laminar and turbulent nature of flow. Below a certain Reynolds number the entire flow is laminar and any disturbance introduced into the flow will be dissipated out by viscosity. The limiting Reynolds number below which the entire flow is laminar is termed the lower critical Reynolds number.

Table 2.1 Some popular shapes and their characteristic lengths

Some of the well-known critical Reynolds number are listed below:

Pipe Bow – Red = 2300: based on mean velocity and diameter d.

Channel Bow – Reh = 1000 (two-dimensional): based on height h and mean velocity.

Boundary layer flow – Ree = 350: based on freestream velocity and momentum thickness в.

Circular cylinder – Rew = 200 (turbulent wake): based on wake width w and wake defect.

Flat plate – Rex = 5 x 105: based on length x from the leading edge.

Circular cylinder – Red = 1.66 x 105: based on cylinder diameter d.

It is essential to note that, the transition from laminar to turbulent nature does not take place at a particular Reynolds number but over a range of Reynolds number, because any transition is gradual and not sudden. Therefore, incorporating this aspect, we can define the lower and upper critical Reynolds numbers as follows.

• Lower critical Reynolds number is that Reynolds number below which the entire flow is laminar.

• Upper critical Reynolds number is that Reynolds number above which the entire flow is turbulent.

• Critical Reynolds number is that at which the flow field is a mixture of laminar and turbulent flows.

Note: It is important to note that when the Reynolds number is low due to large viscosity v the flow is termed stratified Bow, for example, flow of tar, honey etc. are stratified flows. When the Reynolds number

Lift force

is low because of low density, the flow is termed rarefied Bow. For instance, flow in space and very high altitudes, in the Earth’s atmosphere, are rarefied flows.

We saw that there is no net force acting on a circular cylinder in a steady irrotational flow without circulation. It can be shown that a lateral force identical to a lift force on an aerofoil, results when circulation is introduced around the cylinder. When a clockwise line vortex of circulation Г is superposed around the cylinder in an irrotational flow, the stream function [sum of Equations (2.43) and (2.48)]

becomes:

The tangential velocity component at any point in the flow is:

At the surface of the cylinder of radius a, the tangential velocity becomes:

Ve I _ = -2 Vx sin в – —. 1 r=a 2n a

At the stagnation point, Ve = 0, thus:

For Г = 0, the potential flow past the cylinder is symmetrical about both x – and y-directions, as shown in Figure 2.19(a). For this case there is no drag acting on the cylinder.

For Г < 4 n a Vx, two values of в satisfy Equation (2.52). This implies that there are two stagnation points on the surface, as shown in Figure 2.19(b).

When Г = 4 n a Vx, the stagnation points merge on the negative y-axis, as shown in Figure 2.19(c). For Г > 4 ж a Vx the stagnation points merge and stay outside the cylinder, as shown in Figure 2.19(d). The stagnation points move away from the cylinder surface, since sin в cannot be greater than 1. The

radial distance of the stagnation points for this case can be found from:

This gives:

Г ± V7Г2 – (4na Vm)2

One root of this is r > a, and the flow field for this is as shown in Figure 2.19(d), with the stagnation points S and S2, overlapping and positioned outside the cylinder. The second root corresponds to a stagnation point inside the cylinder. But the stagnation point for flow past a cylinder cannot be inside the cylinder. Therefore, the second solution is an impossible one.

As shown in Figure 2.19, the location of the forward and rear stagnation points on the cylinder can be adjusted by controlling the magnitude of the circulation Г. The circulation which positions the stagnation points in proximity, as shown in Figure 2.19(b), is called subcritical circulation, the circulation which makes the stagnation points coincide at the surface of the cylinder, as shown in Figure 2.19(c), is called critical circulation, and the circulation which makes the stagnation points coincide and take a position outside the surface of the cylinder, as shown in Figure 2.19(d), is called supercritical circulation.

To determine the magnitude of the transverse force acting on the cylinder, it is essential to find the pressure distribution around the cylinder. Since the flow is irrotational, Bernoulli’s equation can be applied between a point in the freestream flow and a point on the surface of the cylinder. Bernoulli’s equation for incompressible flow is:

Using Equation (2.52), the surface pressure can be found as follows.

At the surface r — a and Equation (2.51) gives the local velocity at any point on the surface as:

V0| _ — -2 Vm sin в – Г

‘r—a 2n a

Substituting this into Bernoulli’s equation, we get:

that is:

The symmetry of flow about the y-axis implies that the pressure force on the cylinder has no component along the x-axis. The pressure force acting in the direction normal to the flow (along y-axis) is called the lift force L in aerodynamics.

Consider a cylinder of radius a in a uniform flow of velocity Vm, shown in Figure 2.20.

where we have used:

2n 2n

sin ede = sin3 в de = 0.

00

It can be shown that Equation (2.54) is valid for irrotational flows around any two-dimensional shape, not Just for circular cylinders alone. The expression for lift in Equation (2.54) shows that the lift force proportional to circulation Г is of fundamental importance in aerodynamics. Wilhelm Kutta (1902), the German mathematician, and Nikolai Zhukovsky (1906), the Russian aerodynamicist, have proved the relation for lift, given by Equation (2.54), independently; this is called the Kutta-Zhukovskylift theorem (the name Zhukovsky is transliterated as Joukowsky in older Western texts). The circulation developed by certain two-dimensional shapes, such as aerofoil, when placed in a stream can be explained with vortex theory. It can be shown that the viscosity of the fluid is responsible for the development of circulation. The magnitude of circulation, however, is independent of viscosity, and depends on the flow speed Vx, the shape and orientation of the body to the freestream direction.

For a circular cylinder in a potential flow, the only way to develop circulation is by rotating it in a flow stream. Although viscous effects are important in this case, the observed pattern for high rotational speeds displays a striking similarity to the ideal flow pattern for Г > 4naVx,. When the cylinder rotates at low speeds, the retarded flow in the boundary layer is not able to overcome the adverse pressure gradient over the rear surface (downstream of в = 90°) the cylinder. This leads to the separation of the real (actual) flow, unlike the irrotational flow which does not separate. However, even in the presence of separation, observed speeds are higher on the upper surface of the cylinder, implying the existence of a lift force.

A second reason for a rotating cylinder generating lift is the asymmetry to the flow pattern, caused by the delayed separation on the upper surface of the cylinder. The asymmetry results in the generation of the lift force. The contribution of this mechanism is small for two-dimensional objects such as circular cylinder, but it is the only mechanism for the side force experienced by spinning three-dimensional
objects such as soccer, tennis and golf balls. The lateral force experienced by rotating bodies is called the Magnus effect. The horizontal component of the force on the cylinder, due to the pressure, in general is called drag. For the cylinder, shown in Figure 2.20, the drag is given by: /»2п

I pr=a a cos в dd.

0

It is interesting to note that the drag is equal to zero. It is important to realize that this result is obtained on the assumption that the flow is inviscid. In real (actual or viscous) flows the cylinder will experience a finite drag force acting on it due to viscous friction and flow separation.

In Section 2.9 we saw that flow past practical shapes of interest can be represented or simulated with suitable combination of source, sink, free vortex and uniform flow. In this section let us discuss some such flow fields.

2.10.1 Flow Past a Half-Body

An interesting pattern of flow past a half-body, shown in Figure 2.14, can be obtained by combining a source and a uniform flow parallel to x-axis. By definition, a given streamline = constant) is associated

with one particular value of the stream function. Therefore, when we join the points of intersection of the radial streamlines of the source with the rectilinear streamlines of the uniform flow, the sum of magnitudes of the two stream functions will be equal to the streamline of the resulting combined flow pattern. If this procedure is repeated for a number of values of the combined stream function, the result will be a picture of the combined flow pattern.

The stream function for the flow due to the combination of a source of strength – at the origin, immersed in a uniform flow of velocity Vx, parallel to x-axis is:

f = VX r sin в + в.

2п

The streamlines of the resulting flow field will be as shown in Figure 2.14.

The streamline passing through the stagnation point S is termed the stagnation streamline. The stag­nation streamline resembles a semi-ellipse. This shape is popularly known as Rankine’s half-body. The streamlines inside the semi-ellipse are due to the source and those outside the semi-ellipse are due to the uniform flow. The boundary or stagnation streamline is given by:

It is seen that S is the stagnation point where the uniform flow velocity Vx cancels the velocity of the flow from the source. The stagnation point is located at (a, n). At the stagnation point, both Vr and Ve should be zero. Thus:

1

Vr = – r

= Vx cos в + = 0.

2nr

This gives:

–

2nVx’

Therefore, the stream function of the stagnation point is:

– в

fs = Vx r sin в + —.

2n

At the stagnation point S, r = a and в = n, therefore:

–

fs = Vx a sin n +——- n

2n

– – = 2.

The equation of the streamline passing through the stagnation point is obtained by setting ф = = q/2,

resulting in:

A plot of the streamlines represented by Equation (2.46) is shown in Figure 2.14. It is a semi-infinite body with a smooth nose, generally called a half-body. The stagnation streamline divides the field into a region external to the body and a region internal to it. The internal flow consists entirely of fluid emanating from the source, and the external region contains the originally uniform flow. The half-body resembles several shapes of theoretical interest, such as the front part of a bridge pier or an aerofoil. The upper half of the flow resembles the flow over a cliff or a side contour of a wide channel.

The half-width of the body is given as:

q (n — в) 2 nVx

As в ^ 0, the half-width tends to a maximum of hmax = q/(2 Vx), that is, the mass flux from the source is contained entirely within the half-body, and q = (2 hmax) Vx at a large downstream distance where the local flow velocity u = Vx.

The pressure distribution can be found from the incompressible Bernoulli’s equation:

1 2 1 2

p + 2 pu = + 2 pVx

where p and u are the local static pressure and velocity of the flow, respectively.

The pressure can be expressed through the nondimensional pressure difference called the pressure coefficient, defined as:

p – Px 2 pxV.2

where p and px are the local and freestream static pressures, respectively, px is freestream density and Vx is freestream velocity.

A plot of Cp distribution on the surface of the half-body is shown in Figure 2.15. It is seen that there is a positive pressure or compression zone near the nose of the body and the pressure becomes negative or suction, downstream of the positive pressure zone. This positive pressure zone is also called pressure-hill.

The net pressure force acting on the body can easily be shown to be zero, by integrating the pressure p acting on the surface. The half-body is obtained by the linear combination of the individual stream functions of a source and a uniform flow, as per the Rankine’s theorem which states that:

“the resulting stream function ofn potential Bows can be obtained by combining the stream functions of the individual Bows."

The half-body shown in Figure 2.15 is also referred to as Rankine’shalf-body.

The potential function for the flow is:

m

Ф = V^r + — cos в.

It is seen that ф = 0 for all values of в, showing that the streamline ф = 0 represents a circular cylinder of radius r = ^/m/(2nVCXl). Let r = a = ^/m/(2nVCXl). For a given velocity of the uniform flow and a given strength of the doublet, the radius a is constant. Thus, the stream function and potential function

Ve = rde =- V» ( 1 + "T ) sin в.

The flow speed around the cylinder is given by:

VI =1 Ve I = 2 V» sin в.

where what is meant by | is the positive value of sin в. This shows that there are stagnation points on the surface at (a, 0) and (a, n). The flow velocity reaches a maximum of 2 V» at the top and bottom of the cylinder, where в = n/2 and 3n/2, respectively. The nondimensional pressure distribution over the surface of the cylinder is given by:

p – p» = і іPV2 = V2 2pV» »

1 – 4 sin2 в

(2.50)

Pressure distribution at the surface of the cylinder is shown by the continuous line in Figure 2.18. The symmetry of the pressure distribution in an irrotational flow implies that “a steadily moving body experiences no drag.” This result, which is not true for actual (viscous) flows where the body experiences

drag, is known as d’Alembert’s paradox. This discrepancy between the results of inviscid and viscous flows is because of:

• the existence of tangential stress or skin friction and

• drag due to the separation of the flow from the sides of the body and the resulting formation of wake dominated by eddies, in the case of bluff bodies, in the actual flow which is viscous.

The surface pressure in the wake of the cylinder in actual flow is lower than that predicted by irrotational or potential flow theory, resulting in a pressure drag.

Note: For flow past a circular cylinder, there are two limits for the Cp, as shown in Figure 2.18. These two limitsare Cp = +1 and Cp = —3, at the forward and rear stagnation points (at0° and 180°, respectively), and at the top and bottom locations of the cylinder (at 90° and 270°, respectively). At this stage, it is natural to question about the validity of these limiting values of the pressure coefficient Cp for flow past geometries other than circular cylinder. Clarifying these doubts is essential from both theoretical and application points of view.

• The positive limit of +1 for Cp, at the forward stagnation point, is valid for all geometries and for both potential and viscous flow, as long as the flow speed is subsonic.

• When the flow speed becomes supersonic, there will be a shock ahead of or at the nose of a blunt-nosed and sharp-nosed bodies, respectively. Hence, there are two different speeds at the zones upstream and downstream of the shock. Therefore, the freestream static pressure and dynamic pressure

to be used in the Cp relation:

p – p <x>

2 рП>

have two options, where p is the local static pressure. This makes the Cp at the forward stagnation point sensitive to the freestream static and dynamic pressures, used to calculate it. Therefore, Cp = +1 can not be taken as the limiting maximum of Cp, when the flow speed is supersonic.

• The limiting minimum of -3, for the Cp over the cylinder in potential flow, is valid only for circular cylinder. The negative value of Cp can take values lower than -3 for other geometries. For example, for a cambered aerofoil at an angle of incidence can have Cp as low as —6.

• Another important aspect to be noted for viscous flow is that there is no specific location for rear stagnation point on the body. The flow separates from the body and establishes a wake. The separation is taking place at two locations, above and below the horizontal axis passing through the center of the body. Also, these upper and lower separations are not taking place at fixed points, but oscillate around the separation location, because of vortex formation. Therefore, the negative pressure at the rear of the body does not assume a specified minimum at any fixed point, as in the case of potential flow. For many combinations of the geometries and flow Reynolds numbers, the negative Cp at the separated zone of the body can assume comparable magnitudes over a large portion of the wake.

This is a combination of a source and sink of equal strength, situated (located) at a distance apart. The stream function due to this combination is obtained simply by adding the stream functions of source and sink. When the distance between the source and sink is made negligibly small, in the limiting case, the combination results in a doublet.

2.9.2 Doublet

A doublet or a dipole is a potential flow field due to a source and sink of equal strength, brought together in such a way that the product of their strength and the distance between them remain constant. Consider a point P in the field of a doublet formed by a source and a sink of strength q and — g, respectively, kept at a distance ds, as shown in Figure 2.11, with sink at the origin.

By Rankine’s theorem, the velocity potential of the doublet, фо, can be expressed as the sum of the velocity potentials of the source and sink. Thus, we have:

dr

Expanding ln ( 1 +—– ), we get:

But — ^ 1, therefore, neglecting the second and higher order terms, we get the potential function for a r

doublet as:

q dr 2n r

By the definition of doublet, ds ^ 0, therefore:

dr = ds cos в

Hence,

-ds cos в.

Also, for a doublet, by definition, q ds = constant. Let this constant, known as the strength of the doublet be denoted by m, then:

m = q ds

and

In Cartesian coordinates, the velocity potential for the doublet becomes:

Figure 2.12 Doublet with source and sink on the x-axis (source located on the left and sink on the right of the origin). From the above equations for фо, the expression for the stream function fD can be obtained as:

In Cartesian coordinates, the stream function becomes:

ml y

2п У x2 + y2

If the source and sink were placed on the x-axis, the streamlines of the doublet will be as shown in Figure 2.12.

If the source and sink are placed on the y-axis, the resulting expressions for the фо and fD will become:

фО(уу) — 2nr S^n в

m

2п x2 + у2 m

fD(yy) = – 2ПГ cos в

mx 2n yx2 + y2

The streamlines of the doublet will be as shown in Figure 2.13. The expression for the stream function:

can be arranged in the form:

fD(yy) = –

where c = m/(2n), is a constant. This can be expressed as:

о о C X

x2 + y + ———- = 0

Thus, the streamlines represented by ^D(yy) = constant are circles with their centers lying on the x-axis and are tangent to the y-axis at the origin (Figure 2.13). Direction of flow at the origin is along the negative y-axis, pointing outward from the source of the limiting source-sink pair, which is called the axis of the doublet.

The potential and stream functions for the concentrated source, sink, vortex, and doublet are all singular at the origin. It will be shown in the following section that several interesting flow patterns can be obtained by superposing a uniform flow on these concentrated singularities.