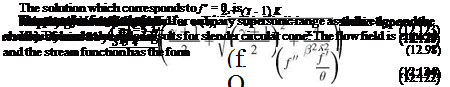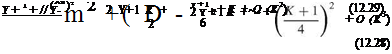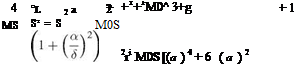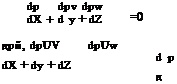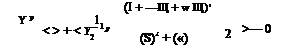Slender Body at Angle of Attack
Grimminger et al. [67], have derived general expressions for the lift and drag of inclined bodies of revolution. They assume that the streamlines remain parallel and leave the surface in a streamwise direction, see Fig. 12.7.
They used the Newtonian formula to calculate the pressure on the wetted part of the body.
Later, the Newtonian theory for slender bodies of revolution at small angle of attack was reported by Cole [66] and Cole and Brainerd [68], as a small perturbation on the solution at zero incidence. Linear equations are obtained with variable coefflcients depending on the zero incidence solution. The results are
where the body shape is given by r — 5F(x), F(1) — 1, as stated before.
Hayes and Probstein [2] extended Cole’s results for non slender bodies.
Cox and Crabtree [3] discuss the case of a cone of circular cross section and the appearance of what is called the vortical layer.
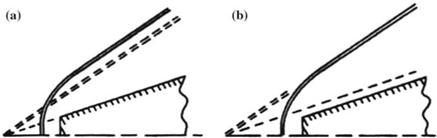
For a cone at zero incidence, the radial surfaces of constant entropy are shown in Fig. 12.8. In the same figure, the corresponding surfaces when a — 20° are shown indicating the existence of rotational flow.
Ferri [69, 71] and Ferri et al. [70] pointed out that the surface of the cone must have constant entropy and there exist a vortical singularity, where the entropy is multi-valued.
The thickness of the vortical layer is shown by Guiraud [72] to be
ev ~ YY—1 exp (——– Y + 1 ) (12.171)
v Y+ 1 a(Y – 1)
where y is a mean value of y downstream of the shock.
Fig. 12.8 Surfaces of constant entropy for flow past cone
Based on Guiraud’s analysis, the surface pressure distributions and the total forces and moment (relative to the nose) acting upon a body of revolution can be calculated in closed form. For slender bodies, Guiraud’s results agree with Cole’s.
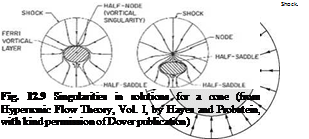
Following Hayes and Probstein [2], singularities in solutions for an elliptic cone at small and large incidences are given in Fig. 12.9.
A topological law, based on a Poincare theory, relates the number of elementary singular points according to the relation
N + F – S + O = 2 (12.172)
where N is the number of nodes, F is the number of foci, S the number of saddle points and O the number of obstacles. For more details, see Ref. [74].
Over two decades, the problem of cones at small and large angles of attack has been studied by many authors, including Tsien [75], Lighthill [76], Young and Sisk [77], Stone [78, 79], Willet [80, 81], Holt [82], Cheng [83, 84], Sychev [85], Munson [86], Woods [87, 88], Melnick [89, 90]. Numerical simulations are discussed by Moretti [91], Dwyer [92] and Fletcher [93]. A comprehensive review can be found in the book by Bulakh [94].
Blunt Body Problems
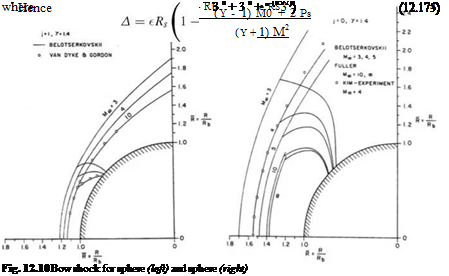
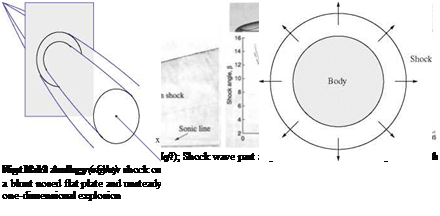
There are two categories, the example for the first is cylinders or cones, while the second is a slender body with a blunt nose, see Fig. 12.10 from Ref. [2].
For the bow shock stand-off distances for spheres and cylinders, approximate analytical relations are given by Hayes and Probstein [2]. For a sphere with a radius Rb and a shock of radius Rs, assuming constant density in the thin layer between the bow shock wave and the body surface
For the case of the circular cylinder
 Y+1, and for a sphere, the stand-off distance becomes
Y+1, and for a sphere, the stand-off distance becomes
Y — 1
A ~ Rs (12.177)
Y + 1
Recent work on theoretical models for stand-off distance is discussed by Olivier in [95].
At the axis, the normal shock wave leads to the largest entropy jump and the entropy decreases as the shock angle approaches the Mach angle. Hence, according to Crocco’s relation, vorticity is generated behind a curved shock.
For a blunt body at angle of attack, the entropy layer and the vortical layer will mix in the neighborhood of the body where the boundary layer is also growing.
The Flow field around a sphere at Mach 10 and Mach 50 are shown in Fig. 12.11.
The analogy of a bow shock on a blunt nosed body and unsteady one – dimensional explosion is sketched in Fig. 12.12.
These complicated flows have been studied over the years. In the series expansion methods, it is assumed that the shock shape is known. The conditions just downstream
of the shock can be obtained from the shock relations and the derivatives of the flow variables may be obtained using the governing equations. Taylor series in terms of the distance from the shock is used to describe the flow field between the shock and the body. Examples of this approach are given by Lin and Rubinov [96], Shen and Lin [97] and Cabannes [98, 99]. The convergence of the Taylor series, near the body is in general questionable as discussed by Van Dyke [100].
Numerical methods are more suitable for such a study as discussed by Hayes and Probstein [2].
Van Dyke [101] used an inverse method integrating the flow equations from the shock to the body by a marching technique, assuming the shock shape to be a conic section, see also Mangler [102]. Good results for stand-off distance for a sphere, in agreement with experimental measurements, are reported for different high Mach numbers. However, the problem is, in general, ill-posed as shown by Vaglio-Laurin [103], where almost indistinguishable shock shapes produce completely different body shapes. Special treatment is required to avoid numerical instabilities.
Another approach to solve the inverse problem was proposed by Garabedian and Lieberstein [104], based on the method of complex characteristics.
First the initial data for a known analytic shock curve are continued into a fictitious three-dimensional space which consists of the real value of one of the independent variables and the complex value of the other. The wave equation can be solved, in a stable manner, by a marching procedure, or by the method of characteristics.
However, any small change in the initial data in the real domain can result in a large change in the complex domain. Lin [105] noticed that the analytic continuation of the initial conditions from real values into the complex domain is itself the solution of an initial value problem for a Laplace equation. For simple closed form analytic shock shapes such as hyperbolas or parabolas for the hypersonic blunt body problem, the initial conditions are continued exactly into the complex domain avoiding any instabilities.
Moreover, Van Dyke [106], pointed out that the computational time of Garabe – dian and Lieberstein method was almost 200 times his straightforward marching procedure.
Inverse methods have been applied to asymmetric flows by Vaglio-Laurin and Ferri [107]. They treated bodies of revolution at small angles of attack by perturbation around a body at zero incidence.
Of course, the usual problem of interest is the direct problem, where the inverse methods can be used via trial and error. Hayes and Probstein [2], considered building up a catalog of solutions, a dangerous philosophy delaying the advances of direct methods.
In the late 50s, Dorodnitsyn proposed a direct method based on integral relations, see also Belotserkovskii and Chushkin [108]. See also Holt [109].
The basic idea is to solve a system of partial differential equations in a domain by dividing the domain into strips and obtain independent integral relations to obtain the solutions of the variables in each strip. Assuming a polynomial variation in one variable of the flow variables between the shock and the body and substituting into the equations of motion, a system of ordinary differential equations is generated and may be integrated numerically across the strips. An initial guess of the shock shape is assumed and the solution is obtained by iteration. Dorodnitsyn [110] has generalized his method, by multiplying the basic equations by a function to obtain the moments of the equations in an attempt to increase the accuracy of the calculations. Notice the analogy with the early boundary layer methods). Many variants exist and for more details see Holt [109].
Perhaps, more interesting are the applications of finite differences (and finite volumes) using relaxation techniques or unsteady approach to steady-state solutions of the governing equations.
Mitchell and McCall [111], calculated the supersonic flow over blunt bodies using the stream function/vorticity formulation where the shock wave was assumed known from experimental measurements. A serious problem was the breakdown of the relaxation procedure in the neighborhood of the sonic line. Hayes and Probstein [2], discussed how to carry the calculations through the sonic region and somewhat beyond the limiting characteristics and established consistency relations used as boundary conditions on the sonic line. These conditions may indicate how the shock shape should be updated to obtain an improved solution. (The supersonic flow field can be always obtained via the method of characteristics).
In such calculations, the shock is fitted. A more attractive approach is the shock capturing, where conservative Euler equations, in primitive variables, are solved explicitly to reach steady-state. There are two main schools, the first is based on explicit artificial viscosity as in the Lax-Wendroff scheme and the second is based on upwind schemes as in the Godunov method. Early applications to hypersonic flows of Lax-Wendroff type scheme was reported by Burstein and Rusanov using his version of the Lax scheme. Applications of Godunov’ schemes are discussed in Holt’s book [109]. Implicit methods to solve the unsteady Euler equations have been developed since then, see for example Richtmeyer and Morton [112]. For recent review of numerical methods for hypersonic inviscid flows see Pletcher et al. [113]. Notice, some of the early methods applied for hypersonic flows have been extended to deal with lower transonic flow regime, for example Garabedian’s complex characteristics and the integral relation method as well as shock fitting and shock capturing techniques for the relaxation method of the stream function equation (see Emmons [114], Steger [115], Hafez and Lovell [116]), and for the unsteady Euler equations (see Hirsch [117], Van Leer [118], Roe [119], Osher [120] for upwind schemes).
To conclude this section, we will discuss briefly the works of Chernyi and Cheng for the slender bodies with blunt noses.
In Chernyi’s method [121], it is assumed that a plane piston starts to move from the nose with a velocity V = Uв, normal to the flow direction, to generate a wedge or a cone of semi-angle в (see also Cox and Crabtree [3]) for the governing integral equations expressing conservation of energy and momentum in the equivalent unsteady flow problem.
The method of Cheng [122], includes also the effect of the entropy layer.
Guiraud [123] treated directly the effect of slight bluntness. Yakura [124] used the inverse problem as discussed in Van Dyke [100]. In Fig. 12.13, in the direct problem,
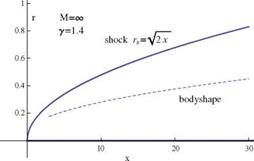
Fig. 12.14 Blunt axisymmetric slender body producing a paraboloidal shock with infinite Mach number and 7 = 1.4
the shock wave is forced away from the body due to bluntness, while in the inverse problem the body must move instead.
Yakura has applied his method also to the axisymmetric problems of the blunted cone that supports a hyperbolidal shock wave and the body that produces a paraboloidal shock wave at M = ro. Yakura’s results are close to those of Sychev [125], see Fig. 12.14.











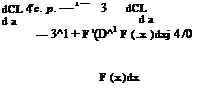
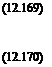



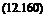 p0 — 1 + "02S’2 p — ІЇ
p0 — 1 + "02S’2 p — ІЇ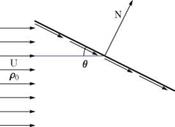
 Fig. 12.3 Newton’s impact theory
Fig. 12.3 Newton’s impact theory

 Fig. 12.6 Sphere in Hypersonic Flow
Fig. 12.6 Sphere in Hypersonic Flow
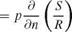 (12.82)
(12.82)