Any two wires of different metals A and B can be used as a thermocouple if connected as in Figure 5.1. When the temperature of the junction, Tjct, is different from the reference temperature TRef, a weak potential difference, E, is generated at the terminals +/-.
The value of E depends on the materials A and B and on the difference between reference temperature and junction temperature:
E=T (a-z)T
J yRef
where eA and eB are the thermoelectric power or Seebeck coefficients of the two metals.
For small temperature differences, the following linear equation can be used:
E = (єА – Єв){Т"}а — TRef ) = £AB (T]a — TRef)
where eAB is the Seebeck coefficient of the couple of metals.
Schematic of a thermocouple
The three most common thermocouples are copper-constantan (type T), iron-constantan (type J) and chromel-alumel (type K): the first element of the couple is positive, the negative wire is coded with the red color. All three types are available in pairs of coated wires with a minimum diameter of 25 pm. For reasons of accuracy and space, the minimum diameter possible should be chosen taking into consideration that wires with a diameter less than 75 pm are very weak.
■ Copper-constantan (type T, color codes: blue and red): eAB и 40 pV/K, Tmax = 300°C. Neither wire is magnetic. Junctions can be obtained by welding or brazing with usual welders.
■ Iron-constantan (type J, color codes: white and red): eAB и 50 [pV/K], Tmax = 650°C. Iron is magnetic. The junction can be obtained by welding or brazing with usual welders. The couple iron-constantan can generate a galvanic electromagnetic force: it cannot be used in the presence of water.
■ Chromel-alumel (type K, color codes: yellow and red): eAB и 40 pV/K, Tmax = 1100°C. Alumel is magnetic. The junction can be obtained by welding or brazing with silver, at the higher temperatures iron must be used. This couple generates electrical signals when subjected to deformation.
To measure higher temperatures the following thermocouples may be used:
■ Platinum-platinum/rhodium: Tmax = 1650°C
■ Iridium-ruthenium/iridium: Tmax = 2100°C
■ Tungsten-tungsten/molybdenum: Tmax = 3200°C.
Thermocouples can be purchased ready-made or can be made in the laboratory from pairs of wires using a specific thermocouple welder or any suitable welder for fine wires.
The reference temperature can be controlled in several ways:
■ melting ice is widely used in laboratory because it is accurate and inexpensive: a thermos can maintain 0°C for several hours if filled with crushed ice and water;
■ systems are available that provide reference temperatures controlled electronically; these devices are not as stable as melting ice, and require periodic calibration but are very easy to use;
■ other instruments use as a reference the temperature that is generated within the container, assuming that this is not affected by environmental conditions;
■ in less accurate measures the room temperature can be used as a reference.
The main difficulty encountered in the use of thermocouples is the need for the junction and the wires not to disturb the temperature distribution in the wall. It is advisable to check the effect of the thermal conductivity of the wires and the heat transfer to or from the junction to determine the measurement error in each individual application:
■ In a metal wall, the junction can be welded directly to the metal, taking care not to alter the character of the surface and its emissivity. The simple method of welding the junction to the surface and spreading out the wires parallel to the surface in an isothermal layer, to minimize losses by conduction, can be adopted only in incompressible flows; such a system, causing shock waves in supersonic flows and disrupting the surrounding boundary layer, would completely alter the local temperature conditions: in this case, the sensor should be placed inside the body.
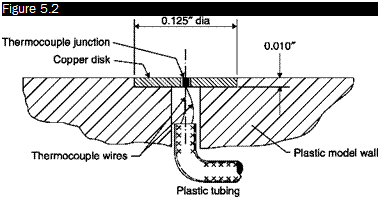
■ With models made of insulating material good results can be obtained by using discs of copper or silver, approximately 3 mm in diameter and 0.25 mm thick, inserted into the wall flush with the surface. Figure 5.2 shows this arrangement of the thermocouple used for measurements in a supersonic field: the disk can easily reach the temperature of the surface and quickly follow any change in temperature due to its low heat capacity. The influence of radiation can be reduced by covering the insert with a thin layer of lacquer having an emissivity similar to that of the wall.
Measurement of temperature of a plastic wall with a thermocouple











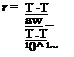


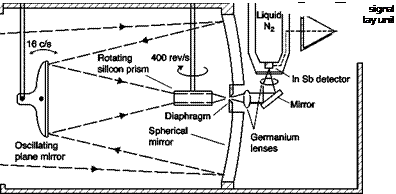


 different from that of the exciting light, for example (Figure 5.4), a paint excited with ultraviolet light (280 г 390 nm) emits red light (580 г 630 nm). This feature makes it possible to filter the incident light and measures only the emitted light. Paints have been developed to measure temperatures ranging from ambient up to 1000°C.
different from that of the exciting light, for example (Figure 5.4), a paint excited with ultraviolet light (280 г 390 nm) emits red light (580 г 630 nm). This feature makes it possible to filter the incident light and measures only the emitted light. Paints have been developed to measure temperatures ranging from ambient up to 1000°C.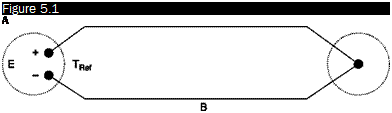
![Подпись: Figure 4.37 20 40 60 80 X mm Source: [6]](/img/3131/image263_2.gif)