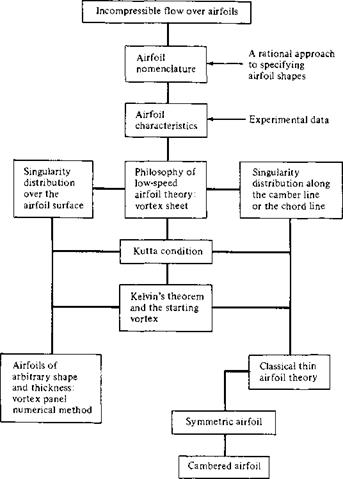
Center of Pressure
From Equations (1.7) and (1.8), we see that the normal and axial forces on the body are due to the distributed loads imposed by the pressure and shear stress distributions. Moreover, these distributed loads generate a moment about the leading edge, as given by Equation (1.11). Question: If the aerodynamic force on a body is specified in terms of a resultant single force R, or its components such as N and A, where on the body should this resultant be placed? The answer is that the resultant force should be located on the body such that it produces the same effect as the distributed loads. For example, the distributed load on a two-dimensional body such as an airfoil produces a moment about the leading edge given by Equation (1.11); therefore, N’ and A! must be placed on the airfoil at such a location to generate the same moment about the leading edge. If A! is placed on the chord line as shown in Figure 1.18, then N’ must be located a distance xcp downstream of the leading edge such that
MLE — (xcp)N
![]() [1.20]
[1.20]
In Figure 1.18, the direction of the curled arrow illustrating M[E is drawn in the positive (pitch-up) sense. (From Section 1.5, recall the standard convention that aerodynamic moments are positive if they tend to increase the angle of attack.) Examining Figure 1.18, we see that a positive N’ creates a negative (pitch-down) moment about the leading edge. This is consistent with the negative sign in Equation (1.20). Therefore, in Figure 1.18, the actual moment about the leading edge is negative, and hence is in a direction opposite to the curled arrow shown.
|
|
|

![]() Equivalent ways of specifying the force-and-moment system on an airfoil.
Equivalent ways of specifying the force-and-moment system on an airfoil.
In Figure 1.18 and Equation (1.20), xcp is defined as the center of pressure. It is the location where the resultant of a distributed load effectively acts on the body. If moments were taken about the center of pressure, the integrated effect of the distributed loads would be zero. Hence, an alternate definition of the center of pressure is that point on the body about which the aerodynamic moment is zero.
In cases where the angle of attack of the body is small, sin a ~ 0 and cos a ~ 1: hence, from Equation (1.1), L’ ~ N’. Thus, Equation (1.20) becomes
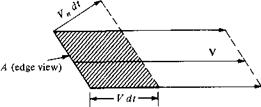
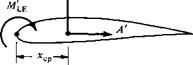
Examine Equations (1.20) and (1.21). As N’ and L’ decrease, xcp increases. As the forces approach zero, the center of pressure moves to infinity. For this reason, the center of pressure is not always a convenient concept in aerodynamics. However, this is no problem. To define the force-and-moment system due to a distributed load on a body, the resultant force can be placed at any point on the body, as long as the value of the moment about that point is also given. For example, Figure 1.19 illustrates three equivalent ways of specifying the force-and-moment system on an airfoil. In the left figure, the resultant is placed at the leading edge, with a finite value of { . In the middle figure, the resultant is placed at the quarter-chord point, with a finite value of M’y4. In the right figure, the resultant is placed at the center of pressure, with a zero moment about that point. By inspection of Figure 1.19, the quantitative relation between these cases is
MhE = — — L + Мсц = —xcpL [1.22]
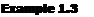 In low-speed, incompressible flow, the following experimental data are obtained for an NACA 4412 airfoil section at an angle of attack of 4°: q = 0.85 and cmx/4 = —0.09. Calculate the location of the center of pressure.
In low-speed, incompressible flow, the following experimental data are obtained for an NACA 4412 airfoil section at an angle of attack of 4°: q = 0.85 and cmx/4 = —0.09. Calculate the location of the center of pressure.
Solution
From Equation (1.22),
![]()
|
|
|
|
-^cp 1 (^c/4/^00^ ) 1 Off, г/4
c 4 (L’/q^c) 4 с,
![]() _ 1 (-0.09)
_ 1 (-0.09)
“4 0.85
(Note: In Chapter 4, we will learn that, for a thin, symmetrical airfoil, the center of pressure is at the quarter-chord location. However, for the NACA 4412 airfoil, which is not symmetric, the center-of-pressure location is behind the quarter-chord point.)











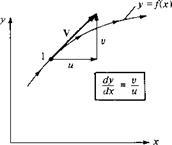
 Consider the velocity field given by и = y/(x2 + y2) and v = —x/(x2 + y2). Calculate the equation of the streamline passing through the point (0, 5).
Consider the velocity field given by и = y/(x2 + y2) and v = —x/(x2 + y2). Calculate the equation of the streamline passing through the point (0, 5).
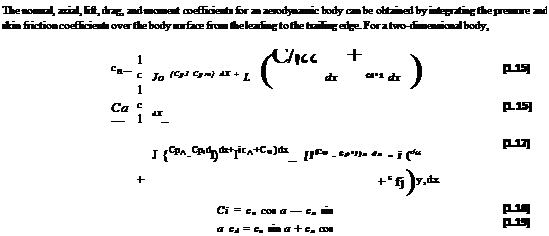
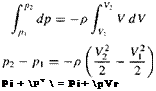 or
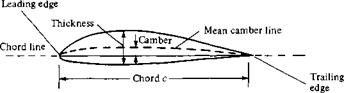
or When first introduced, this airfoil was labeled the GA (W)-l airfoil, a nomenclature which has now been superseded. (From Reference 16.)
When first introduced, this airfoil was labeled the GA (W)-l airfoil, a nomenclature which has now been superseded. (From Reference 16.)


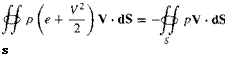 [8.7]
[8.7]