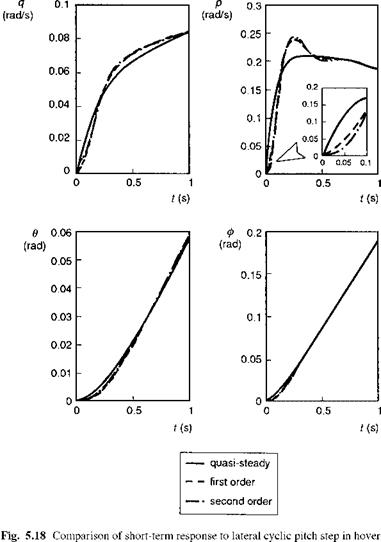
Flying qualities: objective assessment and criteria development
Experience has shown that a large percentage, perhaps as much as 65%, of the life-cycle cost of an aircraft is committed during the early design and definition phases of a new development program. It is clear, furthermore, that the handling qualities of military helicopters are also largely committed in these early definition phases and, with them, much of the mission capability of the vehicle. For these reasons, sound design standards are of paramount importance both in achieving desired performance and avoiding unnecessary program cost. ADS-33 provides this sound guidance in areas of flying qualities, and the authority of the new standards is anchored in a unique base ofadvanced simulation studies and in-flight validation studies, developed under the TTCP collaboration.
(From the TTCP* Achievement Award, Handling Qualities Requirements for Military Rotorcraft, 1994)
6.1 General Introduction to Flying Qualities
In Chapter 2, the Introductory Tour of this book, we described an incident that occurred in the early days of helicopter flying qualities testing at the Royal Aircraft Establishment (Ref. 6.1). An S-51 helicopter was being flown to determine the longitudinal stability and control characteristics, when the pilot lost control of the aircraft. The aircraft continued to fly in a series of gross manoeuvres before it self-righted and the pilot was able to regain control and land safely. The incident highlighted the potential consequences of poor handling qualities – pilot disorientation and structural damage. In the case described the crew were fortunate; in many other circumstances these consequences can lead to a crash and loss of life. Good flying qualities play a major role in contributing to flight safety. But flying qualities also need to enhance performance, and this tension between improving safety and performance in concert is ever present in the work of the flying qualities engineer. An arguable generalization is that military requirements lean towards an emphasis on performance while civil requirements are more safety oriented. We shall address this tension with some fresh insight later in this chapter, but first we need to bring out the scope of the topic.
The ‘original’ definition of handling qualities by Cooper and Harper (Ref. 6.2),
Those qualities or characteristics of an aircraft that govern the ease and precision with which a pilot is able to perform the tasks required in support of an aircraft role
|
still holds good today, but needs to be elaborated to reveal the scope of present day and future usage. Figure 6.1 attempts to do this by illustrating the range of influences – those external to and those internal to the aircraft andpilot. This allows us to highlight flying qualities as the synergy between these two groups of influencing factors. To emphasize this point, it could be argued that without a complete description of the influencing factors, it is ambiguous to talk about flying qualities. It could also be argued that there is no such thing as a Level 1 or a Level 2 aircraft, in the Cooper-Harper parlance. The quality can be referenced only to a particular mission (or even mission task element (MTE)) in particular visual cues, etc. In a pedantic sense this argument is hard to counter, but we take a more liberal approach in this book by examining each facet, each influencing factor, separately, and by discussing relevant quality criteria as a sequence of one-dimensional perspectives. We shall return to the discussion again in Chapter 7.
In the preceding paragraph, the terms handling qualities and flying qualities have deliberately been used interchangeably and this flexibility is generally adopted throughout the book. At the risk of distracting the reader, it is fair to say, however, that there is far from universal agreement on this issue. In an attempt to clarify and emphasize the task dependencies, Key, as discussed in Ref. 6.4, proposes a distinction whereby flying qualities are defined as the aircraft’s stability and control characteristics (i. e., the internal attributes), while handling qualities are defined with the task and environment included (external influences). While it is tempting to align with this perspective, the author resists on the basis that provided the important influence of task and environment are recognized, there seems no good reason to relegate flying to be a subset of handling.
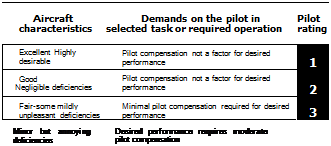
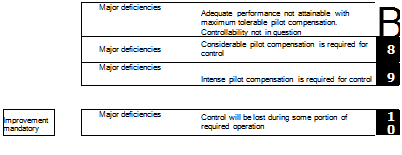
In the structure of current Civil and Military Requirements, good flying qualities are conferred to ensure that safe flight is guaranteed throughout the operational flight envelope (OFE). The concept of flying quality requires a measurement scale to judge an aircraft’s suitability for role, and most of the efforts of flying qualities engineers over the years have been directed at the development of appropriate scales and metrics, underpinned and substantiated by flight test data. The most developed and widely recognized quality scale is that due to Cooper and Harper (Ref. 6.2). Goodness, or quality, according to Cooper-Harper, can be measured on a scale spanning three levels (Fig. 6.2). Aircraft are normally required to be Level 1 throughout the OFE (Refs 6.5, 6.6); Level 2 is acceptable in failed and emergency situations but Level 3 is considered unacceptable. The achievement of Level 1 quality signifies that a minimum required standard has been met or exceeded in design, and can be
 |
|||
|
|||
|
|||
|
|
||
 |
|||
![]()
expected to be achieved regularly in operational use, measured in terms of task performance and pilot workload. Compliance flight testing is required to demonstrate that a helicopter meets the required standard and involves clinical measurements of flying qualities parameters for which good values are known from experience. It also involves the performance of pilot-in-the-loop MTEs, along with the acquisition of subjective comments and pilot ratings. The emphasis on minimum requirements is important and is made to ensure that manufacturers are not unduly constrained when conducting their design trade studies. Establishing the quality of flying, therefore, requires objective and subjective assessments which are the principal topics of Chapters 6 and 7 respectively.
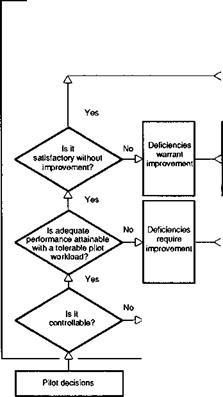
We refer to the subjective pilot ratings given on the Cooper-Harper scale as handling qualities ratings (HQRs). HQRs are awarded by pilots for an aircraft flying an MTE, and are determined by the pilot following through the decision tree shown in Fig. 6.2, to arrive at his or her rating based on their judgement of task performance achieved and pilot workload expended. The task performance requirements will have been set at desired and adequate levels and the pilot should have sufficient task cues to support the judgement of how well he or she has done. In a well-defined experiment this will usually be the case, but poorly defined flight tests can lead to increased scatter between pilots on account of the variations in perceived performance (see Chapter 7 for more discussion on this topic). Task performance can be measured, be it flight path accuracy, tracking performance or landing scatter and the results plotted to give a picture of the relative values of flying quality. The other side of the coin, pilot workload, is much more difficult to quantify, but we ask test pilots to describe their workload in terms of the compensation they are required to apply, with qualifiers – minimal, moderate, considerable, extensive and maximum. The scale implies an attempt to determine how much spare capacity the pilot has to accomplish other mission duties or to think ahead and react quickly in emergencies. The dual concepts of ‘attentional demand’ and ‘excess control capacity’ have been introduced by McRuer (Ref. 6.7) to distinguish and measure the contributing factors to the pilot workload. However subjective, and hence flawed by the variability of pilot training and skill, the use of HQRs may seem, along with supporting pilot comment and task performance results, it has dominated flying qualities research since the 1960s. It is recognized that at least three pilots should participate in a flying qualities experiment (preferably more, ideally five or six) and that HQRs can be plotted with mean, max and min shown; a range of more than two or three pilot ratings should alert the flying qualities engineer to a fault in experimental design. These are detailed issues and will be addressed later in Chapter 7, but the reader should register the implied caution; misuse of HQRs and the Cooper-Harper scale is all too easy and too commonly found.
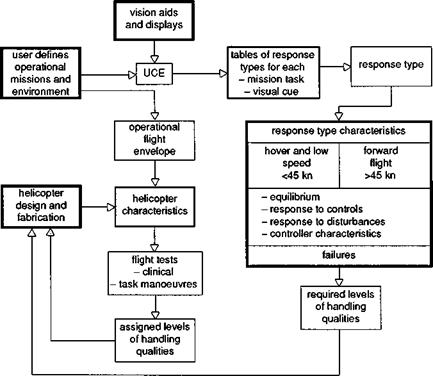
Task performance requirements drive HQRs and give modern military flying qualities standards, like the US Army’s ADS-33C (Ref. 6.5), a mission orientation. The flying qualities are intended to support the task. In a hierarchical manner, ADS-33C defines the response types (i. e., the short-term character of response to control input) required to achieve Level 1 or 2 handling qualities for a wide variety of different MTEs, in different usable cue environments (UCE) for normal and failed states, with full and divided pilot attention. Criteria are defined for both hover/low speed and forward flight, in recognition of the different MTEs and related pilot control strategies in the two operating regimes. Within these flight phases, the criteria can be further related to the level of aggressiveness used by the pilot in attacking a manoeuvre or MTE. At a deeper level, the response characteristics are broken down in terms of amplitude and frequency range, from the small amplitude, higher frequency requirements set by criteria like equivalent low-order system response or bandwidth, to the large amplitude manoeuvre requirements set by control power. By comparison, the equivalent fixed – wing requirements, MIL-F-8785C (Ref. 6.6), take a somewhat different perspective, with flight phases and aircraft categories, but the basic message is the same – how to establish flying quality in mission-related tasks. The innovations of ADS-33 are many and varied and will be covered in this chapter; one of the many significant departures from its predecessor, MIL-H-8501A, is that there is no categorization according to aircraft size or, explicitly, according to role, but only by the required MTEs. This emphasizes the multi-role nature of helicopters and gives the new specification document generic value. Without doubt, ADS-33 has resulted in a significant increase in attention to flying qualities in the procurement process and manufacturing since its first publication in the mid-1980s, and will possibly be perceived in later years as marking a watershed in helicopter development. The new flying qualities methodology is best illustrated by Key’s diagram (Ref. 6.8) shown in Fig. 6.3.
In this figure the role of the manufacturer is highlighted, and several of the ADS – 33 innovations that will be discussed in more detail later in this chapter are brought out, e. g., response types and the UCE.
|
Fig. 6.3 Conceptual framework for handling qualities specification (Ref. 6.8) |
In a similar timeframe to the development of ADS-33C, the revision to the UK’s Def Stan 00970 was undertaken (Ref. 6.9). This document maintained the UK tradition of stating mandatory requirements in qualitative terms only, backed up with advisory leaflets to provide guidance on how the characteristics may be achieved. An example of the 970 requirements, relating to response to control inputs, reads













 (a)
(a)