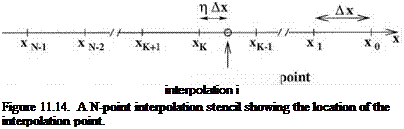
As an example on the use of extrapolation and interpolation in large-scale computing, the problem of scattering of plane acoustic waves by a cylinder in two dimensions is considered. Let the diameter of the cylinder be D. The governing equations are

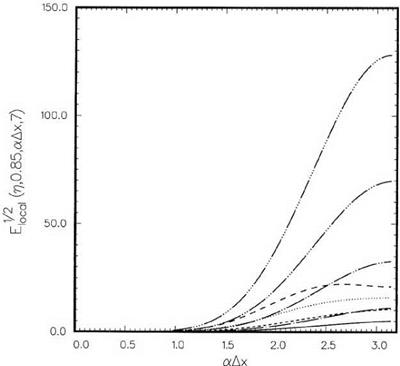
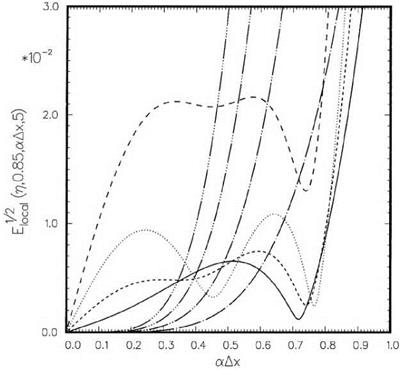
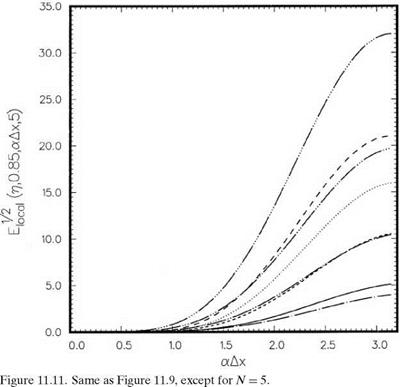
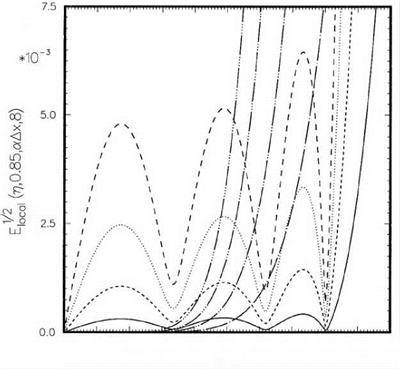
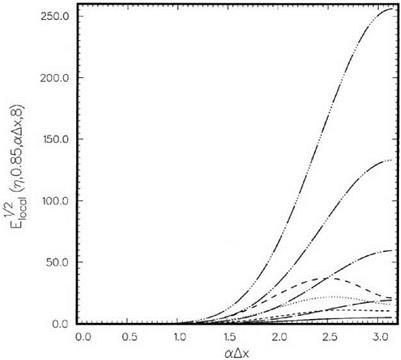
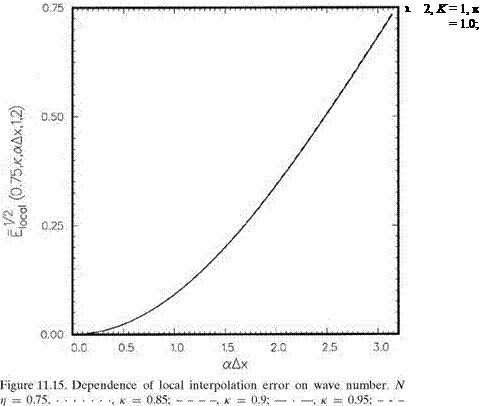
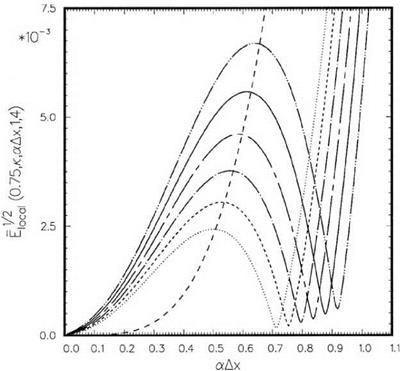
n = 0.75…………….. , к = 0.85;———– , к = 0.9; — • —, к = 0.95;————- , к
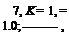 к = 1.05;————- , к = 1.1;——– , Lagrange polynomials interpolation.
к = 1.05;————- , к = 1.1;——– , Lagrange polynomials interpolation.
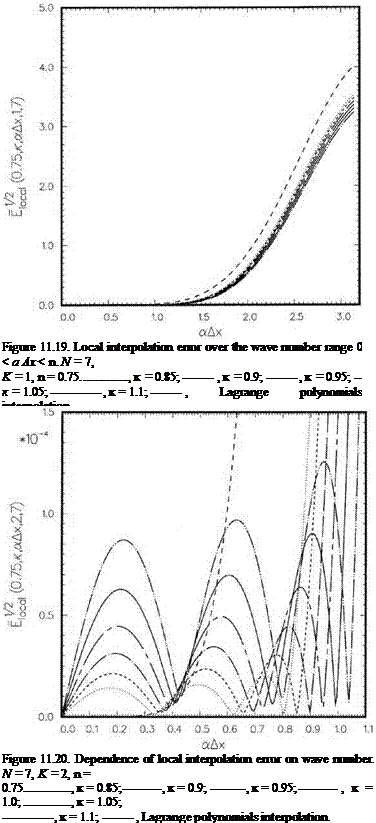
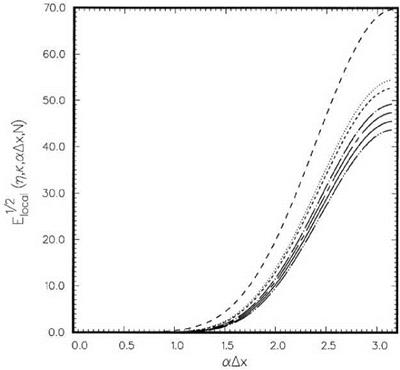
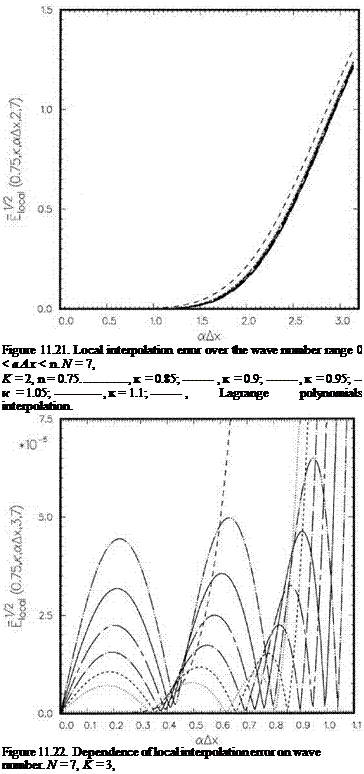
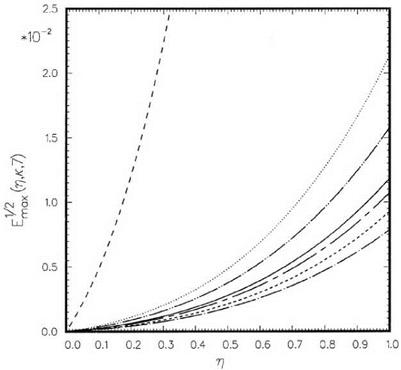
П = 0.75…………….. , к = 0.85;———– , к = 0.9;———- , к = 0.95;———— , к = 1.0;——– ,
к = 1.05;————- , к = 1.1;——– , Lagrange polynomials interpolation.
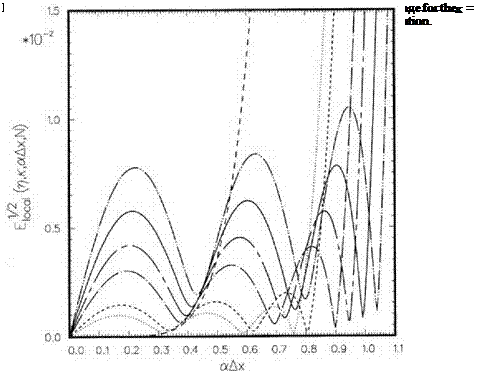
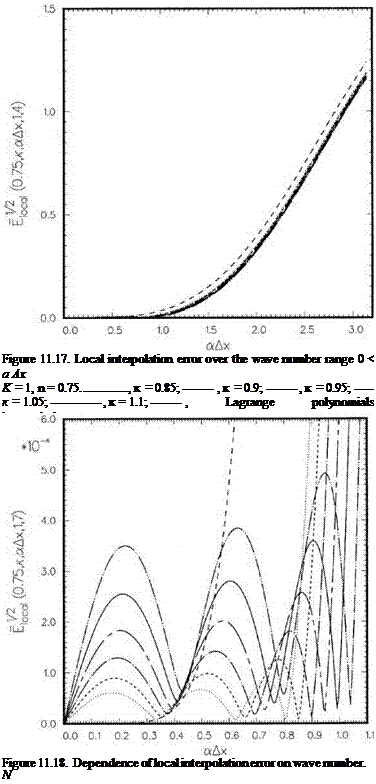
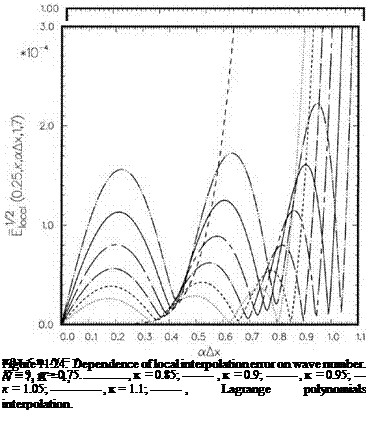
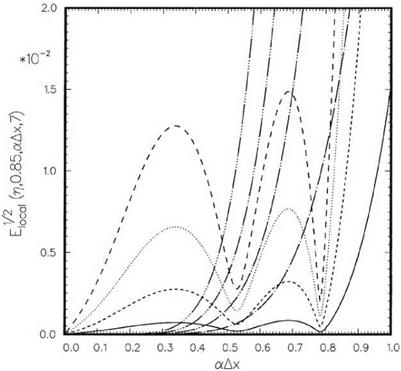
П = 0.25……………. , к = 0.85;——— , к = 0.9;———– , к = 0.95;———— , к = 1.0;
к = 1.05;————- , к = 1.1;———- , Lagrange polynomials interpolation.
the linearized Euler equations. In dimensionless form, they may be written as (with respect to length scale D, velocity scale a0 (speed of sound), time scale Dl a0, density scale p0, and pressure scale p0 a02).
d U d E d F
dt + 3^*" dy
where
|
p
|
|
u
|
|
v
|
|
U=
|
1
і______
|
, E =
|
P
0
u _
|
, F =
|
0
P
v
|
On the surface of the cylinder, the boundary condition is V n = 0, where n is the unit normal to the surface. It can be shown easily that an equivalent form of the boundary condition is
¥ = 0- (11.35)
d n
Eq. (11.34) maybe discretized on a Cartesian mesh using the dispersion-relationpreserving scheme. The scattered sound field may be found by time marching the numerical solution to a time periodic state. However, because the cylinder has a curved surface, a special boundary treatment is needed to enforce boundary condition (11.35). For this purpose, the ghost point method has been extended to treat
Figure 11.26. Cartesian boundary treatment of curved wall surfaces.
arbitrarily curved wall boundaries (see Kurbatskii and Tam, 1997). As an illustration of the boundary treatment, consider the curved boundary shown in Figure 11.26. First, the boundary curve is approximated by line segments joining the intersection points of the computation mesh and the wall boundary. For instance, the curved surface between points A and B in Figure 11.26 is replaced by a straight-line segment. G2 is a ghost point. A ghost value of pressure is assigned to G2 to enforce boundary condition (11.35). The enforcement point is at E; G2E is perpendicular to AB. Since dp/дx and dp/дy are not known, except on the mesh points, their values at A and B are found by extrapolation from the points at (Г, 2′, 3′, 4′, 5′, 6′, 7′) and (1, 2, 3, 4, 5,6,7), respectively. The corresponding values at E are then calculated by interpolation from those at A and B. Once дp/дх and дp/ду are found at E, Eq. (11.35) can be enforced readily.
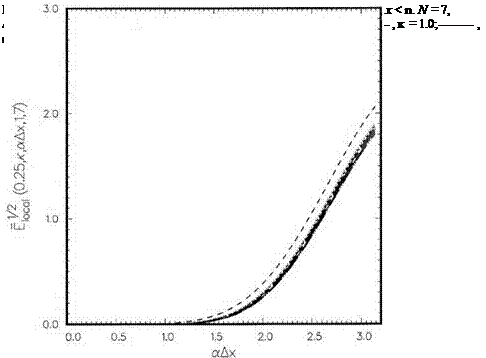
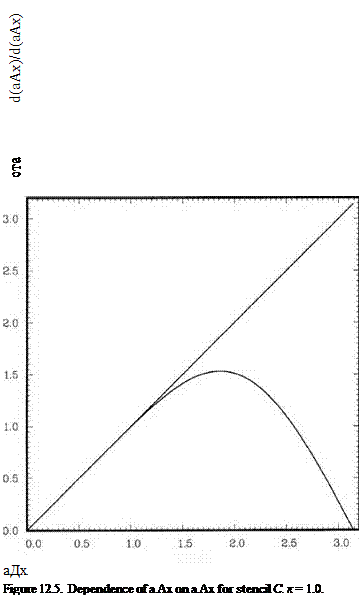
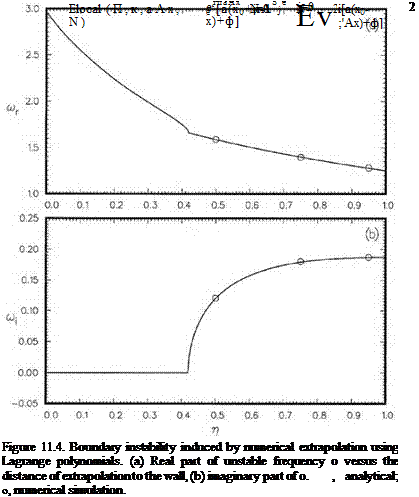
To show the impact of the extrapolation scheme used on the computed results of the scattered waves, a computation domain of 320 x 320 with Ax = Ay = D/32 is used in the solution of the scattering problem. The wavelength of the incoming acoustic waves is equal to 8 Ax. The method of numerical treatment of incoming plane acoustic waves of Section 10.1 is followed in the computation. Because of the special boundary treatment needed to enforce the curved wall boundary conditions, the accuracy of the computed scattered wave is greatly influenced by the extrapolation formula used. Figure 11.27 shows the computed zero pressure contours of the scattered waves at the beginning of a cycle when the Lagrange polynomials extrapolation method is used in the computation. Shown in dotted lines are the zero pressure contours of the exact solution. It is obvious that there are significant differences between
|
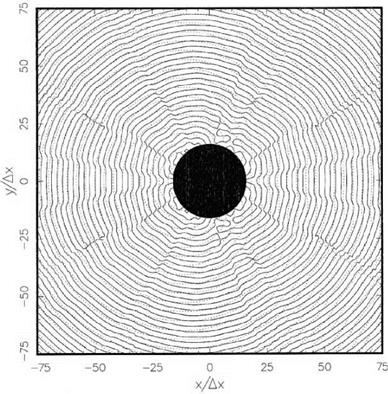
Figure 11.27. Zero pressure contours of the scattered sound field at the beginning of a cycle.
Lagrange polynomials are used for extrapolation.——- , numerical results;………….. , exact
solution.
|
the two sets of contours. It is not difficult to understand why there are such large discrepancies. Wave number analysis indicates that, at 8 mesh points per wavelength, the Lagrange polynomials extrapolation method would give rise to large errors. Such errors contaminate the entire computed scattered wave field.
Figure 11.28 is an identical computation using the optimized extrapolation scheme with an added constraint. Clearly, there is excellent agreement between the numerical results and the exact solution. This is, of course, not surprising since the optimized extrapolation as well as the time marching algorithm are designed to yield fairly accurate results for waves with wavelengths of eight mesh spacings or longer.
EXERCISES [13] [14]
Determine the matrix system by which optimized extrapolation coefficients, Sj, can be calculated. It is suggested that the averaged spacing between adjacent stencil points, A, be used as the length scale.
11.2. Consider two-dimensional interpolation using a rectangular stencil of N by M mesh points. To find the interpolated value at a point P with coordinates (x0, y0), one may first find the values of the function at the intersection of line AA’ (see Figure 11.29) and the mesh lines by interpolation in the y direction. The next
step is to interpolate along AA’ for the value of the function at P. The alternative is to interpolate in the x direction first. That is, the values of the function at the intersection points on the line BB’ with the mesh lines are found by interpolation first. Then the values are interpolated along BB’ to obtain the value of the function at P. Show that the interpolated value at P is the same independent of which direction the interpolation is performed first.

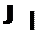 |
 |
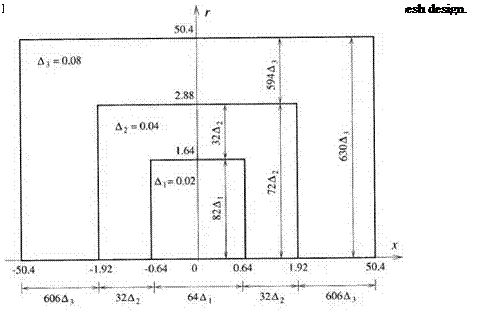
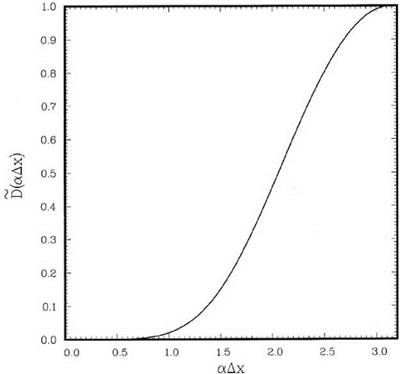
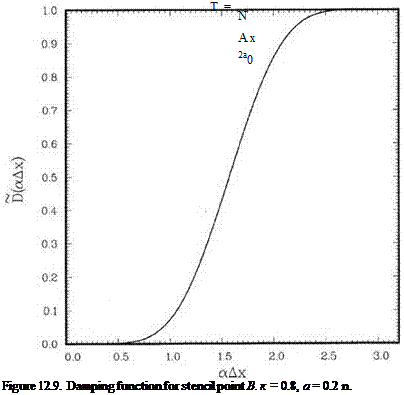
Many aeroacoustics problems involve multiple length and time scales. This should not be difficult to understand. For, in addition to the intrinsic sizes and scales of the noise sources, the acoustic wavelength is an inherent length scale of the problem. In many instances, the length scale of the noise source differs greatly from the acoustic wavelength. This leads to a large disparity in length scales as in classical multiscales problems. For example, in supersonic jet noise, Mach wave radiation is generated by the instability waves of the jet flow. The instability waves are supported by the thin shear layer of the jet. In the region near the nozzle exit, the averaged shear layer thickness is about 0.1D, where D is the jet diameter. The acoustic wavelength, on the other hand, is two or more jet diameters long. Thus, there is an order of magnitude difference between those characteristic lengths. In sound scattering problems, the length scale of the surface geometry of the scatterers may be much smaller than the acoustic wavelength. This occurs very often in edge scattering and diffraction problems. A concrete example is the radiation of fan noise from a jet engine inlet. The acoustic wavelength could be much longer than the radius of the lip of the engine inlet. To obtain an accurate numerical solution of the inlet diffraction problem, a fine mesh is needed around the lip region. Oftentimes, an aeroacoustics problem becomes a multiscales problem because of the change in the physics governing the different parts of the computational domain. An example is the shedding of vortices at the edge of a resonator or a sharp edge of a solid body induced by high-intensity incident sound waves. Away from the solid surface, the fluid is nearly inviscid, but close to the wall, the viscosity effect dominates. The oscillatory motion of the incident sound waves induces a very thin Stokes layer on the solid surface. The Stokes layer rolls up at the corner of a solid surface to form vortices that shed periodically. To simulate the vortex shedding process, therefore, it is necessary to use very fine mesh close to the solid surface and around the corner to resolve the Stokes layer. But away from the solid surface, a coarse mesh with 7 mesh points per acoustic wavelength is all that is needed to capture the sound waves accurately using the 7-point stencil dispersion-relation-preserving (DRP) scheme.
Computationally, a very effective way to treat a multiscales problem is to use a multisize mesh. Figure 12.1 shows a typical multisize mesh. In this example, the mesh size changes by a factor of two across the mesh-size-change interface. A factor-of-2 change in the mesh size is not an absolute necessity. It is recommended because a
Figure 12.1. Special stencils for use in the mesh-size-change buffer regions. •, mesh points at which finite difference approximation of spatial derivative is to be found; x, stencil points; o, points used for interpolation.
 larger change may result in a very strong artificial discontinuity inside the computational domain. On the other hand, a smaller change may require several steps of changes to achieve the same total change in mesh size. This will give rise to a large number of mesh-size-change interfaces, which is not desirable.
larger change may result in a very strong artificial discontinuity inside the computational domain. On the other hand, a smaller change may require several steps of changes to achieve the same total change in mesh size. This will give rise to a large number of mesh-size-change interfaces, which is not desirable.
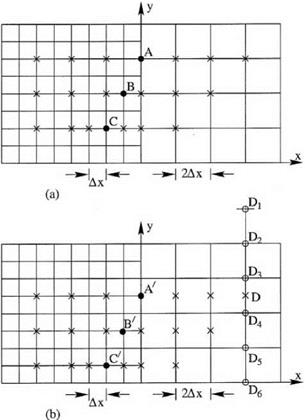
The time step used in a computation is dictated very often by the choice of spatial mesh size. Recall that numerical instability requirements link At, the time step, to the mesh size Ax. If a single time step marching scheme such as the Runge- Kutta method is used, then At is dictated by the smallest size mesh of the entire computational domain. This results in an inefficient computation. The optimum situation is to use a At consistent with the local numerical stability requirement. In such an arrangement, most of the computation is concentrated in regions with fine meshes, as it should be. In the coarse mesh region, the solution is updated only occasionally with a much larger time step. This type of algorithm is referred to as “multi-size-mesh multi-time-step” schemes. If the mesh-size change is a factor of 2 across the mesh block interface, the time step should also change by a factor of 2 to maintain numerical stability. For multilevel time marching schemes such as the DRP scheme, the use of multiple time steps with a factor-of-2 change between adjacent mesh blocks is easy to arrange. Figure 12.2 shows such an arrangement in which the computed solution advanced in steps of At in the fine mesh region and in steps of 2 At in the coarse mesh region.
In carrying out a multi-size-mesh multi-time-step computation, the computation scheme to be used in each of the uniform mesh blocks is the same as if there is a single
size mesh throughout the entire computation domain. The exception is for a narrow buffer region at the block interface. In the buffer region, special stencils are to be used so that information on the solution can be transmitted through without significant degradation. Also, note that any surface of discontinuity, no matter whether it is a mesh-size-change interface or an internal or external boundary, is a likely source of short spurious numerical waves. To suppress the generation of spurious short waves, special artificial selective damping stencils should be incorporated in the computation scheme for mesh points adjacent to the block interface. The design of these special stencils is given in the next three sections.












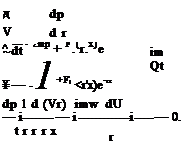
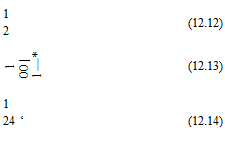
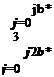 Suppose the solution is known at time level n (see Figure 12.2), the solution in the fine mesh region may be advanced by a time step At to time level (n + 1 /2) in the usual way. Once this is completed, the next step is to advance the solution to time level (n + 1) in both the fine and coarse mesh regions. It is straightforward to carry out this step in the coarse mesh region by using the solution on time levels n, (n – 1), (n – 2), and (n – 3). However, for points in the buffer region on the fine mesh side, the stencils extend into the coarse mesh region. There is no information at the (n + 1/2) time level at these points on the coarse mesh side. To provide the needed information of the solution, it is necessary to compute the solution at the time level (n + 1 /2) for the first two rows or columns of the mesh point on the coarse mesh side based on the solution at time levels n, (n – 1), (n – 2), and (n – 3). To advance the solution by a half time step as shown in Figure 12.2, the following four-level scheme may be used:
Suppose the solution is known at time level n (see Figure 12.2), the solution in the fine mesh region may be advanced by a time step At to time level (n + 1 /2) in the usual way. Once this is completed, the next step is to advance the solution to time level (n + 1) in both the fine and coarse mesh regions. It is straightforward to carry out this step in the coarse mesh region by using the solution on time levels n, (n – 1), (n – 2), and (n – 3). However, for points in the buffer region on the fine mesh side, the stencils extend into the coarse mesh region. There is no information at the (n + 1/2) time level at these points on the coarse mesh side. To provide the needed information of the solution, it is necessary to compute the solution at the time level (n + 1 /2) for the first two rows or columns of the mesh point on the coarse mesh side based on the solution at time levels n, (n – 1), (n – 2), and (n – 3). To advance the solution by a half time step as shown in Figure 12.2, the following four-level scheme may be used:






 larger change may result in a very strong artificial discontinuity inside the computational domain. On the other hand, a smaller change may require several steps of changes to achieve the same total change in mesh size. This will give rise to a large number of mesh-size-change interfaces, which is not desirable.
larger change may result in a very strong artificial discontinuity inside the computational domain. On the other hand, a smaller change may require several steps of changes to achieve the same total change in mesh size. This will give rise to a large number of mesh-size-change interfaces, which is not desirable.
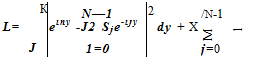 (11.16)
(11.16)![Подпись: sin4K sin[(N-1)K ] 1 “I 4 N-1 2 sin3K sin[(N-2)K ] 1 3 N-2 2 sin2K sin[(N-3)K ] 1 2 N-3 2 sin К sin[(N-4)K ] N-4 1 2 sin 2K ' ' 2 sin К К 1 2 ■ ■ 1 1 1 0](/img/3131/image958_0.gif)
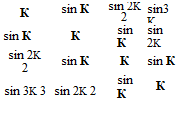
![Подпись: sin[(N-1)K] sin[(N-2)K ] N-1 N-2 1 1 1](/img/3131/image960_0.gif)
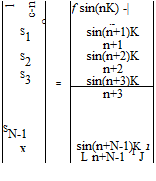 (11.19)
(11.19)